5. Плоскорадиальный фильтрационный поток идеального газа по закону Дарси

Плоскорадиальный поток имеет место в круговом пласте радиусом R_K, в центре которого имеется совершенная скважина радиусомr_e(Рис.9). Характеристику такого потока найдем, зная характеристики подобного потока несжимаемой жидкости.

1. Распределение давленияв потоке несжимаемой жидкости определяется по формуле

. (3.24)

По этому же закону будет распределяться в фильтрационном потоке газа функция Лейбензона

. (3.24) *

Подставив в (3.24)* выражение (6.18) для функции Лейбензона, получим закон распределения давления Р(r) в потоке идеального газа

. (6.26)

С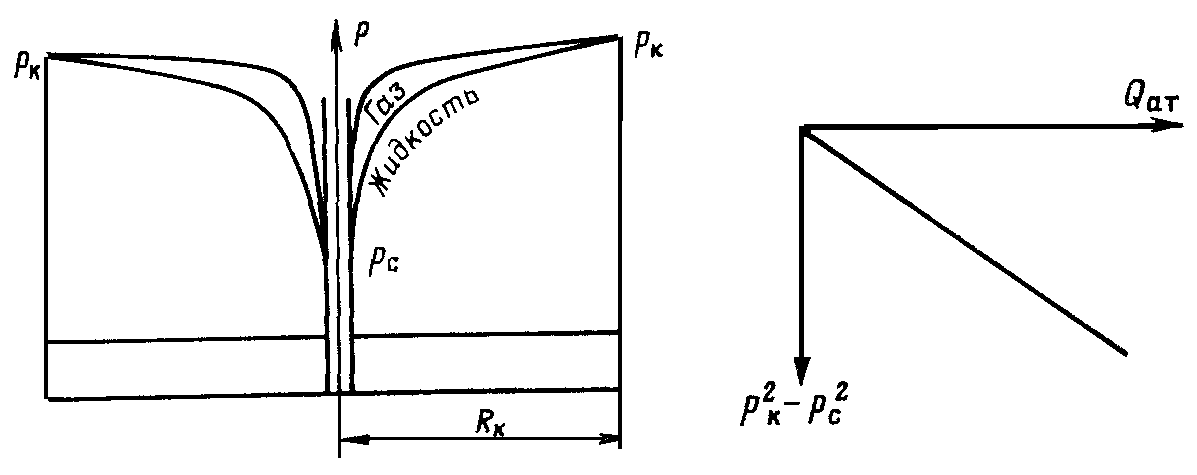равнение кривых Р(r) для несжимаемой жидкости и идеального газа показывает (при одинаковых граничных условиях), что в газовом потоке имеет место резкое падение давления вблизи забоя скважины и весьма малое вдали от нее (рис. 37).

Рис. 37 Рис. 38

2. Изменение градиента давления при плоскорадиальной фильтрации несжимаемой жидкости определяется формулой

. (3.25)

В случае установившейся фильтрации газа по такому же закону будет изменяться функция Лейбензона:

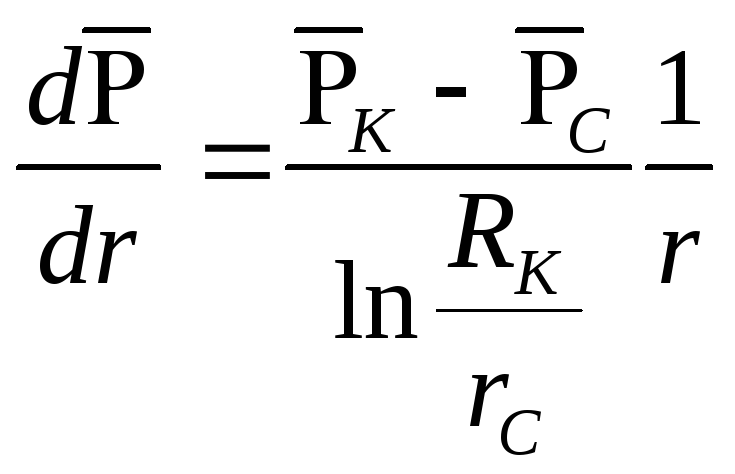. (3.25)*

Переходя от функции Лейбензона (6.18) к давлению, получим

,

откуда

. (6.27)

Из (6.27) следует, что градиент давления вблизи забоя скважины резко возрастает как за счет уменьшения r, так и за счет падения давления Р.

3. Дебит газовой скважины получим, подставив в формулу Дюпюи (3.27) вместо объемного расхода Qсжимаемой жидкости массовый расходQ_mгаза и вместо давления Р функцию Лейбензона

, (3.27)*

или . (6.28)

Индикаторная диаграмма при фильтрации газа строится в координатах Q_АТии при установившемся потоке имеет прямолинейный характер (Рис. 38).

Если представить

,

тогда выражение для дебита газа (6.28) можно представить так:

. (6.28)*

Уравнение (6.28)* в координатах Qи(индикаторная диаграмма) представляет собой параболу с осью, параллельной оси дебитовQ(рис.39). Ветвь параболы, изображенная пунктиром, практического значения не имеет.

Рис. 39

4. Скорость фильтрации несжимаемой жидкости определяется по формуле

. (3.26)

В плоскорадиальном потоке газа так же будет изменяться массовая скорость фильтрации

, (3.26)*

или

,

откуда

. (6.29)

5. Определим средневзвешенное пластовое давление

.

В нашем случае ;dV_П=2rhmdr, а давление Р(r) определяется по формуле (6.26). Тогда

Полученный интеграл не берется в конечном виде и вычисляется приближенно. Получаем приближенное выражение для в виде:

. (6.30)

Расчеты по формуле (6.30) показывают, что в круговом пласте близко к контурному, т.е.. Это объясняется значительной крутизной воронки депрессии при притоке газа к скважине.