3.7. Пример расчета многопролетной статически определимой балки
Многопролетной (шарнирной) балкой называется "СОС", состоящая из ряда однопролетных и консольных балок, соединенных между собой шарнирами. В большинстве случаев на практике возведение многопролетных балок выгодно с точки зрения снижения расхода материалов. Ниже приводится пример расчета многопролетной статически определимой балки (рис. 3.6):
1. Кинематический анализ:
А. W = 3×6 – 3×3 – 2×2 −5 = 0, система может быть неизменяемой;
Б. Структурный анализ: диск АВ вместе с диском "земля" образует единый диск, который соединен с диском СОЕВН с помощью трех непараллельных и непересекающихся в одной точке стержней. Система в целом неизменяема.
2. Определение опорных реакций и реакций связей. Заменим внутренние (шарниры В,С) и внешние (заделка А, шарнирно-подвижные опоры D,G) связи их реакциями, которые будут представлять собой неизвестные пока сосредоточенные воздействия. После этого расчленим нашу систему на элементы. Рассматривая каждый элемент с учетом их совместной работы, определим опорные реакции и реакции связей.
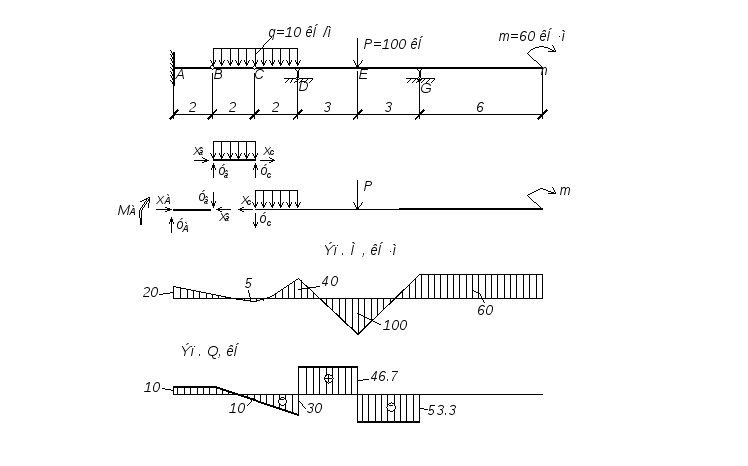
Рис.3.6
Начнем
с ВС:
Рассмотрим СDЕGН:
Проверка:
Перейдём к AB:
3. Построение эпюры изгибающих моментов.
Имеем шесть (AB,ВС,СD,DЕ,ЕG,GН) силовых участков.
Участок АВ:
Начало силового участка примем в сечении "А":
Рис.3.7
Если же за начало силового участка принять сечение "В" (это приводится здесь для доказательства того, что выбор начала участка не влияет на окончательную эпюру):
Рис.3.8
Участок ВС:
Начало консоли примем в точке "В".
Рис.3.9
Участок СD:
Начало участка в сечении "С" (очевидно, что сечение "О" пока началом участка быть не может).
Рис.3.10
Участок DЕ:
Начало силового участка примем в сечении "О".
Рис.3.11
Участок DE:
Начало силового участка примем в сечении "D".
Рис.3.12
Участок ЕG:
Начало силового участка примем в сечении "G".
Рис.3.13
Окончательно получим эпюру моментов, изображенную на рис. 3.6
4. Построение эпюры поперечных сил.
Первоначально рассмотрим силовые участки с линейной эпюрой моментов.
Участок GН:
Эпюра моментов параллельна базису (оси участка), поэтому тангенс угла наклона эпюры моментов, а значит и поперечная сила на этом участке равны нулю.
Участок ЕG: Участок DЕ:
Участок АВ. Участок ВС.
Рис. 3.16 Рис. 3.17
Участок СD.
Рис.3.18
Окончательная эпюра Q изображена на рис.3.6
5. Построение эпюры продольных сил.
Отсутствие горизонтальных составляющих всех реакций позволяет сделать вывод о том, что продольные усилия на всех силовых участках отсутствуют.
6. Общая статическая проверка.
Рис. 3.19
3.8. Пример статического расчета простейшей рамы
1. Кинематический анализ приведенной ниже (рис. 3.20) расчетной схемы:
А. W = 3×3 – 3×2 – 2×0 −3=0, система может быть неизменяемой.
Б. Структурный анализ: диск ДВСО соединен с так называемым диском "земля" посредством шарнира D и стержня (в сеч. А); линия действия стержня не проходит через шарнир. Таким образом, мы имеем дело с неизменяемой системой.
Рис 3.20
2. Определение опорных реакций:
Проверка:
3. Построение эпюры изгибающих моментов
Участок AВ:
Рис 3.21
Участок ВС: Участок ВО:
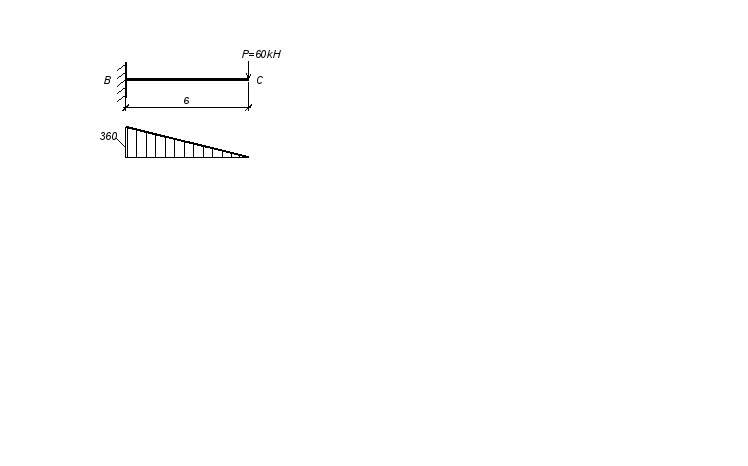
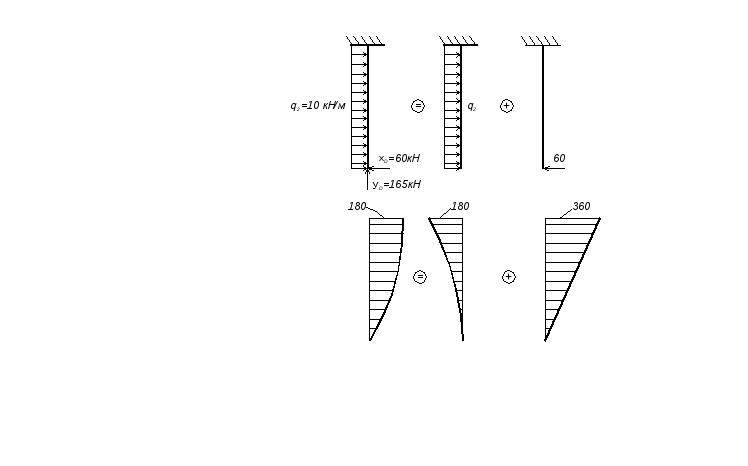
рис. 3.22
Рис 3.23
Статическая проверка правильности построения эпюры моментов (необходимая, но недостаточная).
4. Построение эпюры поперечных сил
Участок АВ:
Q = (q × 6)/2 + (−540 − 0)/6 = −75 кН;
Q = −(q × 6)/2 + (−540 − 0)/6 =−105 кН.
Участок ВD:
Для определения ориентации этого участка в системе знаков вышеуказанной (см. п.3.5) формулы повернем участок ВD таким образом, чтобы распределенная q действовала сверху вниз. Тогда М = М , М = М :
Q = (q × 6)/2 + (180−0)/6 = 60 кН;
Q = −30 + 30 = О.
Участок ВС:
Q = 360/6 = 60 кН.
5. Построение эпюры продольных сил.
Узел В с точки зрения изгибающих моментов, как было показано ранее (см. рис.3.24), находится в равновесии. Тоже самое должно быть и в"стане" продольных и поперечных сил. Именно на этом базируется методика построения эпюры продольных сил.
Продольное усилие в стержне ВО определяется при рассмотрении равновесия узла "В"
Рис. 3.25
Отсутствие продольных сил в стержнях АВ и ВС очевидно:
Рис. 3.26
6. Общая статическая проверка правильности построения эпюр внутренних усилий.
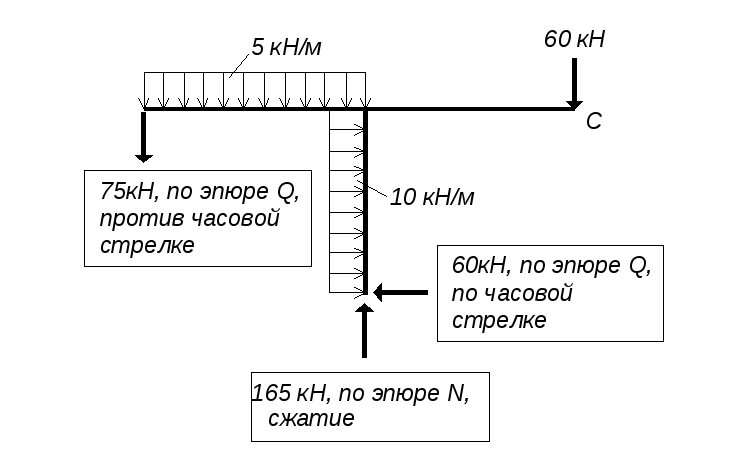
Рис.3.27
