2.2. Определение величины, характеризующей количество степеней свободы произвольной системы.

Классификация систем по этому признаку

W=3×3 – 3×1 – 2×1 – 4 =0

Формула П.Л.Чебышева:

W=3D – 2Ш – 3П – С, где

W − количество степеней свободы,

D − количество простейших дисков,

Ш − количество простых шарниров,

П − количество простых припаек,

С − количество опорных стержней.

Рис.2.10

Перейдем к классификации систем по величинам их степеней свободы.

1. W > 0 − система изменяема (механизм). Непосредственно ее использование воз­можно лишь после добавления W связей.

Рис.2.11

2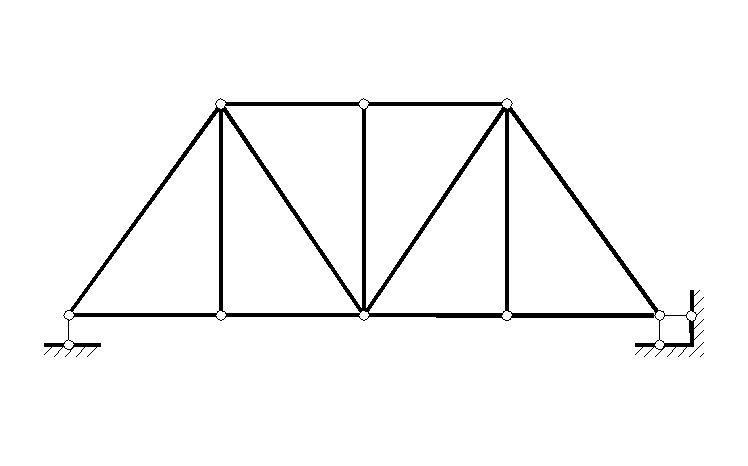.W = 0 − система при разумной расстановке связей может быть неизменяемой.

Необходим дополнительно структурный анализ.

Рис.2.12

3. W< 0 − система имеет лишние связи (гово­рят, что она статически неопределима) и при разумной расстановке этих связей может быть неизменяемой. Также необходим струк­турный анализ.

Рис.2.13

Для проведения структурного анализа необходимо ознако­мить с основными принципами образования неизменяемых и мгно­венно изменяемых систем.

2.3. Основные принципы образования

неизменяемых и мгновенно изменяемых систем

Таблица 2.1

Неизменяемые системы	Мгновенно изменяемые системы
1. Узел, присоединенный к диску при помощи двух стержней, не лежащих на одной прямой	Стержни лежат на одной прямой
2. Один диск присоединен к другому при помощи трех стерж­ней, оси которых не пересека­ются в одной точке и все три одновременно не параллельны	Оси трех стержней параллельны или пересекаются в одной точ­ке
3. Диск, присоединенный к дру­гому одним шарниром и стерж­нем, ось которого не проходит через шарнир	Ось стержня проходит через шарнир
4. Три диска, соединенных меж­ду собой при помощи трех шар­ниров, не расположенных на од­ной прямой	Все три шарнира лежат на од­ной прямой
5. Три диска соединены при помощи шести стержней. Два пересекающихся стержня можно заменить фиктивными шарнирами Ф(1)	Фиктивные шарниры Ф(1) лежат на одной прямой.

2.4 Примеры проведения кинематического анализа

ЗАДАЧА 1.

Решение:

1.Определяем количество степеней свободы заданной системы:

W = 3×16 – 3×0 – 2×22 − 4 = 0

Связей достаточно для того, чтобы система была геометрически неизменяемой.

Рис. 2.14

2. Проведем структурный анализ. Диски 1−2,2−3,3−1 согласно принципа 4 (см.табл.2.1) образуют еди­ную неизменяемую систему. К ней

присоединен узел 4 (принцип 1). Диски 1−2−3−4 согласно прин­ципа 2 образуют единую неизменяемую систему с основанием ("зе­млей"). Аналогично образуется неизменяемая система 6−10−9−5, которая согласно принципа 2 образует единую неизменяемую сис­тему с вышеописанным диском. Окончательно имеем дело с не­изменяемой системой.

ЗАДАЧА 2.

Рис. 2.15

Решение:

1. W = 3×8 – 3×0 − 2×10 − 4

Система М.Б.Н.

2. Проведем структурный анализ.

Налицо три диска: 1-2-3, 3-4-5 и так называемый диск "земля". Диск 1-2-3 соединен с "землей" с помощью двух стержней, пересекаю­щихся в точке 1 (фиктивный шарнир Ф(1)), а 3-4-5 с "землей" посред­ством двух стержней, пересекающих­ся в точке 5 (второй фиктивный шарнир Ф(2)). Три диска (1-2-3, 3-4-5 и "земля") соединены с помощью трех шарниров (Ф(1), Ф(2) и 3), лежащих на одной пря­мой. Система мгновенно изменяема (согласно принципа 4).

ЗАДАЧА 3.

Решение:

1. W = 3×6 – 3×0 – 2×5 − 7 = 1 Система изменяемая, в структурном анализе нет необходимости.

Рис 2.16

ЗАДАЧА 4.

Рис 2.16

Решение:

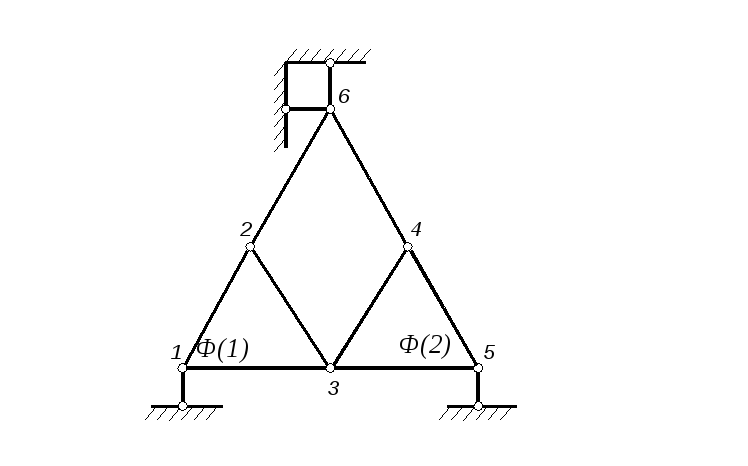
1. W = 3×6 – 3×1 – 2×5 − 5 = 0

Система может быть неизменяемой.

2. Проведем структурный анализ.

Диск 5-6 вместе с "землей" об­разует единую неизменяемую систе­му, к которой с помощью двух стержней 5-2 и 1-2 присоединен узел 2 (система неизменяема сог­ласно принципа 1). Аналогично присоединен узел 3. Система неиз­меняемая, а значит дальнейший ее расчет возможен.