Рахман П.А. - Кодирование информации

72

Вышеприведенный арифметический процессор позволяет с высокой скоростью («за один шаг») выполнять 4 основные операции с любыми двумя заданными элементами поля GF(2m ). Кроме того процессор является «программируемым» с точки зрения используемого в операциях умножения и деления примитивного неприводимого многочлена. Замена примитивного неприводимого многочлена требует лишь перезаписи таблиц степеней и логарифмов, соответствующих требуемому примитивному неприводимому многочлену, в ПЗУ, а с аппаратной точки зрения функциональная схема процессора остается неизменной.

Однако, следует отметить, что на практике, в частности в аппаратных реализациях алгоритмов кодирования и декодирования информации, как правило, примитивный неприводимый многочлен является заданным «раз и навсегда», и, соответственно, перепрограммирование таблиц степеней и логарифмов практически никогда не требуется. Кроме того, в алгоритмах кодирования чаще требуется, в первую очередь, сложение и умножение элементов Галуа, причем для достижения наибольшего быстродействия требуется выполнять одновременно нескольких операций, например, умножить несколько элементов поля GF(2m ) на некоторый другой элемент. В такой ситуации использовать арифметический процессор в качестве умножителя становится накладным с точки зрения быстродействия в силу необходимости многократного обращения к нему. Особенно это становится накладным при умножении элементов поля на некоторый фиксированный элемент поля, который задается как «константа» в том или ином алгоритме.

В такой ситуации для построения быстрых и компактных умножителей выгоднее

умножению (конъюнкции). Для аппаратной реализации таких функции удобнее использовать специализированные программируемые логические матрицы (ПЛМ), содержащие в себе логические элементы «И» с двумя входами и многовходовые сумматоры по модулю 2.

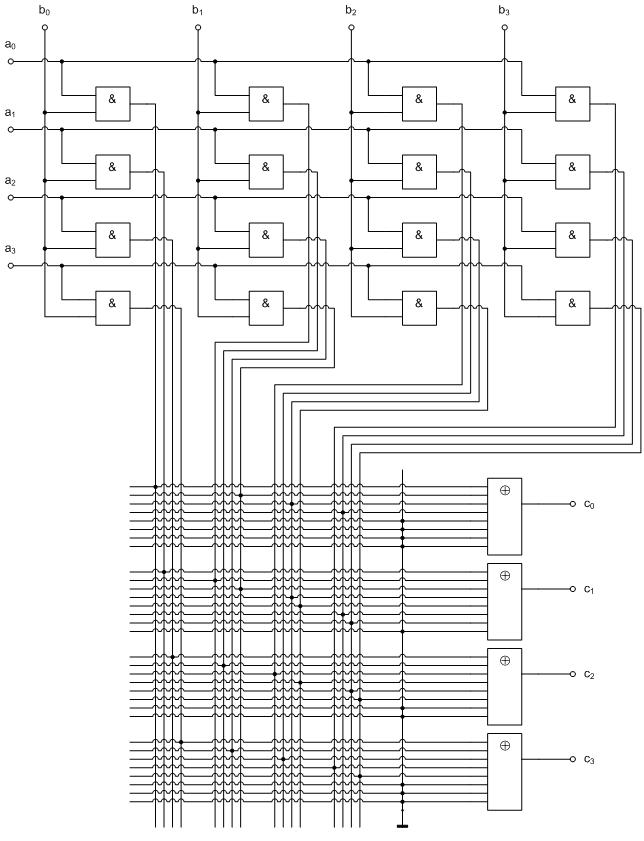
Ниже на рис. 2.4 приведена функциональная схема умножителя элементов поля GF(24 ), образованного на базе примитивного неприводимого многочлена p(x) x4 x 1.

73

Входы сумматоров в соответствии с аддитивными функциями подключаются к выходам логических элементов «И», формирующих соответствующие произведения коэффициентов ai bj. Незадействованные входы сумматоров подключаются к «земле».

Рис. 2.4. Функциональная схема умножителя элементов поля Галуа GF(24 )

на базе специализированной логической матрицы.

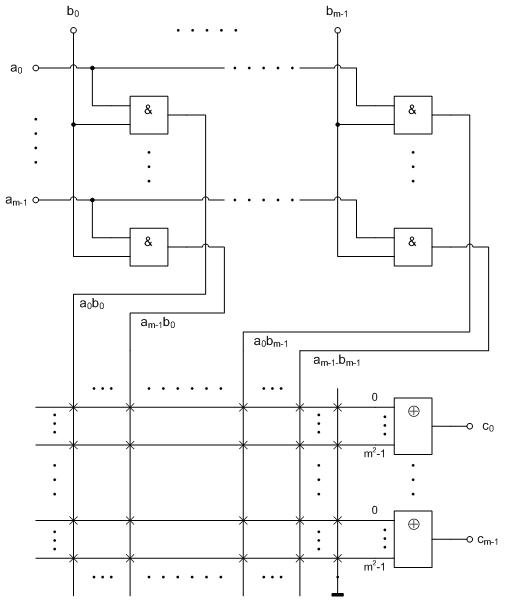
Ниже на рис. 2.5. приведена общая функциональная схема умножителя элементов поля Галуа GF(2m ) на базе специализированной программируемой логической матрицы.

Рис. 2.5. Общая функциональная схема умножителя элементов для полей Галуа GF(2m ) на базе специализированной программируемой логической матрицы.

75

Теперь рассмотрим умножение произвольного элемента a поля Галуа GF(2m ) на

фиксированный элемент b~ этого поля, который является константой в том или ином алгоритме, и определяется еще на этапе проектирования аппаратной реализации алгоритма.

Рассмотрим на примере поля Галуа GF(24 ), образованного при помощи примитивного неприводимого многочлена p(x) x4 x 1 умножение элемента поля на некоторый фиксированный (константный) элемент b~, например, b~ (1111)2 . Тогда аддитивные функции для вычисления коэффициентов многочлена-произведения c(x) значительно упрощаются:

Для аппаратной реализации также можно использовать специализированные программируемые логические матрицы, содержащие в себе многовходовые сумматоры по модулю 2. Ниже на рис. 2.6 приведена функциональная схема умножителя элементов поля GF(24 ), образованного на базе примитивного неприводимого многочлена p(x) x4 x 1,

на фиксированный элемент b~ (1111)2 с использованием ПЛМ. Входы сумматоров в соответствии с аддитивными функциями подключаются к соответствующим линиям коэффициентов ai . Незадействованные входы сумматоров подключаются к «земле».

Рис. 2.6. Функциональная схема умножителя элемента a поля Галуа GF(24 ) на константный элемент b~ (1111)2 на базе специализированной логической матрицы.

76

Следует отметить, что вышеприведенный умножитель можно было бы реализовать в «экономичном» варианте (рис. 2.7), используя двухвходовые логические элементы XOR. Однако, у такого варианта есть существенный недостаток – различные задержки формирования выходных сигналов, ведущие к проблеме «гонок» в цифровых схемах: сигнал на выходе c1 формируется практически сразу же, так как он просто соединен с входной

линией a0 , остальные же сигналы формируются позже из-за задержек на одном (для c2 ),

двух (для c3 ) и на трех (для c0 ) последовательно соединенных логических элементах XOR.

Поэтому ПЛМ хотя и более затратные, зато обеспечивают более или менее равные задержки.

Рис. 2.7. Экономичный вариант функциональной схемы умножения элемента a поля Галуа GF(24 ) на константный элемент b~ (1111)2 .

Приведенный пример умножения элемента поля Галуа GF(24 ) на фиксированный элемент b~ (1111)2 нетрудно обобщить для общего случая умножения элемента поля Галуа

GF(2m ) образованного на базе заданного примитивного неприводимого многочлена p(x) на заданный фиксированный элемент b~.

Ниже на рис. 2.8 также приведена общая функциональная схема «умножителя на константу» для поля Галуа GF(2m ) на базе специализированной ПЛМ.

Рис. 2.8. Общая функциональная схема «умножителя на константу» для полей Галуа GF(2m ) на базе специализированной программируемой логической матрицы.

77

Наконец, заметим, что используя умножитель элементов поля Галуа GF(2m ) на базе специализированной программируемой логической матрицы также можно построить арифметический процессор для поля Галуа GF(2m ), сведя операцию деления элемента a на ненулевой элемент b поля к умножению на обратный элемент b 1 по умножению.

Вычисление обратного элемента по умножению для максимального быстродействия, очевидно, лучше всего опять же осуществлять табличным способом, используя ПЗУ

емкостью 2m m бит. Что касается формирования самой таблицы обратных элементов на этапе проектирования, то это можно осуществлять программным способом, используя расширенный алгоритм Евклида для многочленов, который мы подробно рассматривали

элемент – это единица. Соответственно, многочлен g(x), находимый алгоритмом, и является искомым обратным многочленом по умножению, то есть b 1(x) g(x).

Приведем пример таблицы обратных элементов для элементов поля GF(24 ), представленных для компактности в виде десятичных и двоичных эквивалентов элементов.

Ниже на рисунке 2.9 представлена функциональная схема арифметического процессора для поля Галуа GF(2m ), использующего таблицу обратных элементов по умножению, хранящуюся в ПЗУ и умножитель элементов, который, как было рассмотрено выше, реализуется на базе специализированной программируемой логической матрицы.

В схеме процессора используются два m-битных мультиплексора 2 1. Нижний мультиплексор коммутирует свои входы с выходами логических элементов XOR при управляющем сигнале S1 = 0 (режим операций сложения / вычитания), и с выходами умножителя при S1 = 1 (режим операций умножения / деления). При S1 = 0, управляющий сигнал S0 не играет никакой роли (сложение и вычитание сводится к одной и той же операции «побитового» XOR). При S1 = 1, сигнал S0 управляет верхним мультиплексором, который при S0 = 0 подключает линии bm 1 b0 напрямую к умножителю элементов, что

соответствует операции умножения на операнд b, а при S0 = 1 подключает выходы ПЗУ, преобразующего операнд b в его обратный элемент по умножению, что соответствует операции деления на операнд b. В схеме процессора также предусмотрена цепь обнаружения нулевого делителя (b = 0) в режиме операции деления (S1 = 1 и S0 = 1).

79

Конечное поле Галуа GF(28) в технологии помехоустойчивого кодирования.

Расширенное конечное поле Галуа GF(28 ) является частным случаем расширенных конечных полей GF(2m ) характеристики 2 и имеет широкое применение в технологиях помехоустойчивой передачи и хранения информации благодаря тому, что основной единицей информации в вычислительной технике является байт. Байт состоит 8 битов и с помощью него можно представить 256 различных символов, и поле GF(28 ) также содержит 256 элементов, которые можно представить в виде 8-разрядных двоичных чисел.

Яркие примеры использования арифметики поля Галуа GF(28 ) : помехоустойчивое кодирование с применением кодов Рида-Соломона для хранения информации на оптических дисках с данными – Data CD-ROM и при передаче информации в стандарте цифрового телевещания DVB – Digital Video Broadcasting.

Поле Галуа GF(28 ) содержит 256 элементов:

неприводимого многочлена 8-й степени. В технологии помехоустойчивого кодирования обычно используется примитивный неприводимый многочлен следующего вида:

поля GF(28 ) является элемент (x) x, и при помощи него можно получить все ненулевые

логарифмов можно формировать параллельно с формированием таблицы степеней, используя двоичное или десятичное представление степеней примитивного элемента в качестве индексов таблицы логарифмов:

Под выражением k 1 1 понимается сдвиг двоичного числа влево на один разряд.

Под выражением ( k 1 1) (100011101)2 понимается сдвиг двоичного числа влево на

один разряд с последующей операцией «побитового» XOR результата сдвига с двоичным эквивалентом примитивного неприводимого многочлена.

Примечание. Поскольку в десятичном виде примитивный элемент поля GF(28 )

выглядит как ( )10 2, то будем также обозначать k-ую степень примитивного элемента как

2k , а логарифм от элемента a по основанию примитивного элемента как log2 a.

80

Ниже в таблице 1.1 (в виде матрицы 16 x 16) приведены степени примитивного элемента ( )10 2 поля GF(28 ) , образованного при помощи примитивного неприводимого

многочлена p(x) x8 x4 x3 x2 1. Степени примитивного элемента для компактности приведены в десятичном представлении, и расположены построчно (по 16 в строке), начиная с 0-й степени, и заканчивая 255-й. Заметим, что 255-я степень эквивалентна 0-й степени и равна 1 в силу свойств конечных полей Галуа GF(pm ) : (pm 1) 0 (28 1) 0.

Примечание 1. Для того, чтобы выбрать в таблице требуемую степень 2k , необходимо выбрать строку и столбец таким образом, чтобы сумма индексов строки и столбца (индексы строк приведены в левом заголовочном столбце серого цвета, индексы столбцов – в верхней заголовочной строке серого цвета) была равна показателю степени k.

Таблица 1.1. Таблица степеней 2k для поля Галуа GF(28) .

Также ниже в таблице 1.2 (в виде матрицы 16 x 16) приведены логарифмы по