Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Нефтяной Технический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

razdel2UMK

.pdf

Скачиваний:

Добавлен:

17.03.2015

Размер:

1.08 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 129 10 11 12 > Следующая >>>

Решение.

ТочкаM1(2;−1;3)α1 ;

M2 (1;2;−3) α2

(рис. 2.18). Если вектор

нормаль-

ный вектор плоскости α, проходящей через обе пря-

мые, то N M1M2

и N S , где S ={3;2;−2}. Сле-

={−1;3;−6}.

довательно,

где

M M

Тогда

Рис.2.18

−1

−6

= 6

−20

={6;−20;−11}

j −11

−2

Плоскость α проходит через прямую l1 . Следовательно, точка M1 α. Тогда уравнение плоскости α имеет вид A(x −2)+ B(y +1)+C(z −3)= 0, где N ={A;B;C}. Подставляя координаты вектора N в это уравнение, получим 6 (x −2)−20 (y +1)−11 (z −3)= 0 . Значит, уравнение искомой плоскости имеет вид 6x −20y −11z +1 = 0 .

2.8. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

Геометрические образы (сфера, эллипсоид, гиперболоид, параболоид, цилиндр, конус, …) алгебраического уравнения второй степени

Ax2 + By2 +Cz2 + Dxy + Exz + Fyz + Px +Qy + Rz + H = 0.

(2.42)

Относительно трех переменных x, y, z в прямоугольной декартовой сис-

теме координат называются поверхностями второго порядка.

В данном параграфе рассматриваются некоторые образы уравнения (2.42) при D = E = F = 0. Основным методом изучения поверхности при известном её уравнении является метод сечений, состоящий в определении линии пересечения поверхности с плоскостями, параллельными осям координат.

1) Множество точек пространства R3 , равноудаленных от одной фиксированной ее точки M0 (x0 ; y0z0 ), называется сферой. Её уравнение имеет вид

(x − x0 )2 +(y − y0 )2 +(z −z0 )= R2 .

(2.43)

где точка M0 (x0 ; y0 ;z0 ) - центр сферы, R > 0 - её радиус.

2) Эллипсоидом называется поверхность, определяемая уравнением

(x − x0 )2	+	(y − y0 )2	+	(z −z0 )2	=1.	(2.44)
a2		b2		c2
Числа a, b,c > 0 называются полуосями эллипсоида. Если a, b,c						- раз-

личные числа, то поверхность (рис.2.19) называется трехосным эллипсоидом. Если два из них равны между собой, то эллипсоид является поверхностью вра-

	C
		b	0 b
a	0	Y	a	Y
			a
X

Рис. 2.19

Рис. 2.20

Zщения. При a = b = c эллипсоид вырождается в сферу.

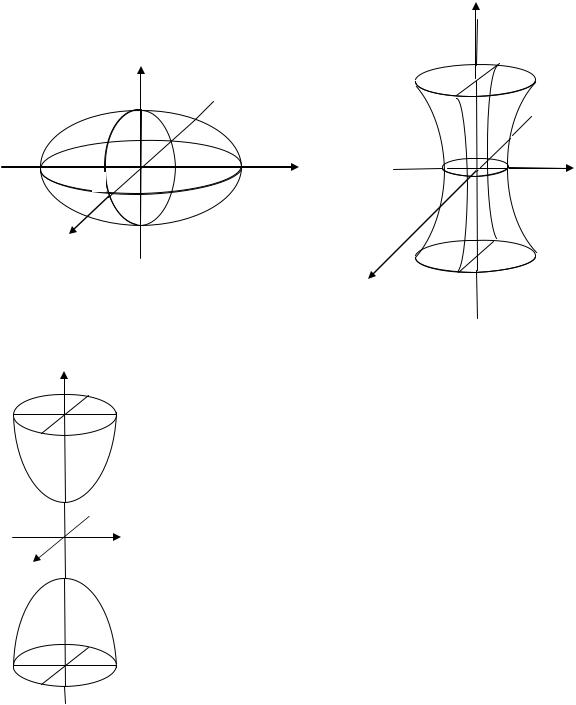
3)Однополостным гиперболоидом (рис.2.20) на-

зывается поверхность, определяемая уравнением

(x − x0 )2

(y − y0 )2

−

(z −z0 )2

=1.

(2.45)

При x0 = y0 = z0 = 0 уравнение (2.45) называется

каноническим уравнением однополостного гиперболои-

да. Гиперболоиды с осями симметрии Ox и Oy задают-

ся уравнениями

x 2

Рис.2.21

−

=1 и

−

2 =1.

(2.46)

4) Двухполостным гиперболоидом (рис. 2.21) называется поверхность,

определяемая уравнением

(x − x0 )2

(y − y0 )2

(z −z0 )2

= −1.

(2.47)

−

При

x0 = y0 = z0 = 0 уравнение (2.47)

называется каноническим урав-

нением двухполостного гиперболоида.

Гиперболоиды с осями симметрии Ox и Oy задаются уравнениями

−

= −1,

(2.48)

−

= −1

5) Эллиптическим параболоидом назы-

вается поверхность, определяемая уравнением

(x − x0 )2

(y − y0 )2

= 2(z −z0 )2

(2.49)

где p,q > 0.

При x0 = y0 = z0 = 0 уравнение (2.49) на-

зывается каноническим уравнением эллиптиче-

ского параболоида (рис. 2.22). Параболоиды с

Рис.2.22

осями симметрии Ox и Oy соответственно за-

даются уравнениями

= 2x ,

(2.50)

+ z

= 2y

Рис.2.23

При p = q уравнения (2.49), (2.50) определяют соответствующие поверх-

ности вращения.

6) Конусом называется поверхность, определяемая уравнением

(x − x0 )2	+	(y − y0 )2	−	(z −z0 )2	= 0.	(2.51)
a2	+	b2	−	c2	= 0.

При x0 = y0 = z0 = 0 уравнение (2.51) называется каноническим уравнением конуса (рис.2.23). Конусы с осями симметрии Ox и Oy соответственно задаются уравнениями

−

= 0 ,

(2.52)

−

= 0 .

При a = b, b = c, a = c в соответствующих уравнениях (2.51), (2.52) образуются круговые конусы.

Примеры решения задач
ПРИМЕР 2.24. Вывести уравнение поверхности, каждая точка которой
расположена вдвое ближе к точке A(2;0;0), чем к точке B(−4;0;0).
Решение. Если S - поверхность, заданная	условиями	задачи,	то
M(x, y, z) S в том и только в том случае, когда ρ(M, B)= 2 ρ(M, A)			или
(x + 4)2 + y2 + z2 = 2 (x −2)2 + y2 + z2 .	Отсюда	получаем

(x + 4)2 + y2 + z2 = 4 ((x − 2)2 + y2 + z2 ) 3x2 − 24x +3y2 +3z2 = 0

или, выделяя полный квадрат в слагаемых, содержащих x , получаем искомое уравнение поверхности в виде (x −4)2 + y2 + z2 =16 . Из него видно, что заданная поверхность S есть сфера радиуса 4 с центром в точке (4;0;0).

ПРИМЕР 2.25. Исследовать форму кривой Г, заданной уравнениями

(x −1)2 + y2 + z2 = 36,
	y + z = 0.

Определить вид её проекции на плоскость Oxy .
Решение. Кривая Г	задана как линия пересечения сферы

(x −1)2 + y2 + z2 = 36 с плоскостью y + z = 0 и, следовательно, есть окружность. Так как центр сферы C(1;0;0) лежит в плоскости сечения y + z = 0, то

центр окружности совпадает с точкой C, а ее радиус равен радиусу сферы, т.е. R = 4. Установим форму проекции окружности Г на плоскость Oxy . Исклю-

			(x −1)2	+ y2 + z2 = 36,	2	+ 2y	2	= 36 , или
чая z из системы				y + z = 0,	получаем (x −1)	+ 2y		= 36 , или
(x −1)2				y + z = 0,
(x −1)2	+	y2	=1. Отсюда заключаем, что искомая проекция – эллипс, главные
36	+	18
36		18

оси которого сонаправлены с осями Ox и Oy, центр находится в точке (1;0), а полуоси равны a = 6, b = 3 2 .

ПРИМЕР 2.26. Методом сечений исследовать форму и построить поверх-

		x	2		y	2
	−			−

ность, заданную уравнением z = 2 1		16			25		.

Решение. В сечении поверхности горизонтальной плоскостью z = h имеем кривую Гh , проекция которой на плоскость Oxy определяется уравнением

		x	2		y	2		x	2		y	2
	−			−			или			+			= 2	−h .	(2.53)

h = 2 1		16			25			16			25

Уравнение (2.53) при h > 2 не имеет решений относительно (x, y). Это означает, что соответствующее сечение пусто, т.е. рассматриваемая поверхность целиком расположена ниже плоскости z = 2. При h ≤ 2 уравнение (2.53)

определяет эллипс с полуосями a = 4 2 −h и b = 5 2 −h , вырождающийся в точку x = y = 0 при h = 2. Заметим, что все эллипсы, получающиеся в сече-

				5	2
4	2				y
4	2
	x2	+	y2	=1	y2 = 25(2 − z)
x	8	+	25 2	=1	y2 = 25(2 − z)
x	8		25 2

x2 =16(2 − z)

Рис. 2.24

ниях поверхности плоскостями x = h ≤ 2, подобны между собой

a	= const =	4
			, при-
		5
b

чем с уменьшением h их полуоси неограниченно и монотонно возрастают. Полученной информации достаточно, чтобы построить эскиз поверхности. Дальнейшее уточнение ее формы можно получить, если рассмотреть сечения координатными плоско-

стями Oxz и	Oyz. Сечение	плоскостью	Oxz : y = 0 дает	кривую
x2 =16(2 −z),	т.е. параболу с	параметром	p =8, вершиной	в точке

x = 0, z = 2 и ветвями, направленными в сторону убывания значений z . Сечение плоскостью Oyz: x = 0 дает параболу y2 = 25(2 −z) с параметром

p = 252 , вершиной в точке y = 0, z = 2 и аналогично направленным ветвями.

Заданная поверхность есть эллиптический параболоид (рис. 2.24).

УЧЕБНО – МЕТОДИЧЕСКИЙ КОМПЛЕКС

РАЗДЕЛ 2 «АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ»

3. Материалы для самостоятельной работы студентов

3.1.КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Виды уравнений прямой на плоскости.

2.Взаимное расположение прямых на плоскости.

3.Кривые второго порядка, их канонические уравнения.

4.Виды уравнений плоскости.

5.Взаимное расположение плоскостей.

6.Виды уравнений прямой в пространстве.

7.Взаимное расположение прямых в пространстве.

8.Взаимное расположение прямой и плоскости.

9.Поверхности второго порядка, их канонические уравнения

3.2. ЗАДАЧИ И УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

3.2.1. Даны две точки A (1;3) и B(4;6). Найти: 1) уравнение прямой AB; 2) угловой коэффициент к этой прямой; 3) угол наклона прямой к оси 0X .

3.2.2. Даны три точки A (0; 4), B(1; − 2), C (5;6). Найти: 1) уравнение

прямой BC; 2) уравнение прямой проходящей через точку A параллельно прямой BC; 3) уравнение прямой проходящей через точку A перпендикулярно прямой BC.

3.2.3.Найти проекцию точки A (− 6; 4) на прямую 4 x −5 y + 3 = 0.

3.2.4.Найти точку B симметричную точке A (−5;13) относительно прямой 2 x −3 y −3 = 0 .

3.2.5.Через точку пересечения прямых x + y −1 = 0 и 2x +3y + 4 = 0 провести прямую: 1) перпендикулярно прямой 3x − y + 7 = 0; 2) параллельно

этой прямой.

3.2.6. Под каким углом прямая y = 2x +3 пересекает ось Ox ?

3.2.7.	Найти угол между прямыми:	1) y = −2x +3 и y = 3x +5; 2)
3x +4y −7 = 0 и 4x −3y +8 = 0 .
3.2.8.	Найти расстояние между	двумя параллельными прямыми

3x + 4y −12 = 0 и 6x +8y + 26 = 0 .

3.2.9. Найти уравнение прямой, проходящей через точку (− 4;3) и удаленной от начала координат на расстояние 5 ед. масштаба.

3.2.10.Даны две противоположные вершины квадрата A(−1;3), C(6;2). Составить уравнения его сторон.

3.2.11.Даны две вершины треугольника A(2;1) и B(4;9) и точка

пересечения его высот N(3;4). Найти уравнение сторон треугольника.

3.2.12. Треугольник ABC задан координатами своих вершин A(2;−2), B(6;1), C(− 2;0). Требуется: 1) написать уравнение стороны AB; 2) написать уравнение высоты CD и вычислить ее длину h ; 3) найти угол ϕ между высотой CD и медианой BM ; 4) написать уравнение биссектрис L1 , L2 внутреннего и внешнего углов при вершине A.

3.2.13.	Составить уравнения сторон треугольника,					зная его		вершину
(4;3), а также		уравнения биссектрисы x + 2y −5 = 0					и	медианы
4x +13y −10 = 0 , проведенных из одной вершины.
3.2.14.	На	прямой	2 x − y −5 = 0	найти	такую	точку	P , сумма
расстояний которой до точек A (− 7;1) и B(−5;5) была бы наименьшей.
3.2.15.	На	прямой	3 x − y −1 = 0	найти	такую точку		P ,	разность
расстояний которой до точек A (4;1) и B(0; 4) была бы наибольшей.

3.2.16. Составить уравнения сторон треугольника, если даны одна из его
вершин B(− 4;−5)	и уравнения двух высот 5 x + 3 y − 4 = 0 и
3 x +8 y +13 = 0 .

3.2.17.Найти уравнения сторон треугольника, зная одну его вершину

С(4; −1), а также уравнения высоты 2 x −3 y +12 = 0 и медианы 2 x + 3 y = 0 ,

проведенных из одной вершины.

3.2.18. Среди прямых, проходящих через точку P (3;0), найти такую, отрезок которой, заключенный между прямыми 2 x − y − 2 = 0, x + y + 3 = 0, делится в точке P пополам.

3.2.19. Точка A (2; −5) является вершиной квадрата, одна из сторон которого лежит на прямой x −2 y −7 = 0. Вычислить площадь этого квадрата.

3.2.20.	Две стороны квадрата лежит	на прямых 5 x −12 y −65 = 0,
5 x −12 y + 26 = 0 . Вычислить его площадь.		квадрата A (2;0) и B(−1; 4).
3.2.21.	Даны две смежные вершины	квадрата A (2;0) и B(−1; 4).

Составить уравнения его сторон.

3.2.22. Луч света направлен по прямой x − 2 y + 5 = 0 . Дойдя до прямой 3 x − 2 y + 7 = 0 луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч.

3.2.23.Составить уравнение прямой, проходящей через точку

пересечения прямых 3 x + y −5 = 0, x − 2 y +10 = 0 и отстоящей от точки C (−1; − 2) на расстоянии d = 5 .

3.2.24. Написать уравнение окружности, проходящей через три точки:

(0;1), (2;0), (3;−1).

3.2.25.Составить уравнение окружности, проходящей через точки (3;1), (−1;3), если ее центр лежит на прямой 3x − y − 2 = 0.

3.2.26.Вычислить расстояние от центра окружности x 2 + y2 = 2x до


прямой,	проходящей			через	точки	пересечения		окружностей
x 2 + y2 +5x −8y +1 = 0, x 2 + y2 −3x + 7y − 25 = 0.
3.2.27.		Составить		уравнение		касательной	к	окружности
(x + 2)2 + (y −3)2			= 25 в точке A(−5;7).
3.2.28.		Дан	эллипс	9x 2 +5y2 = 45. Найти: 1)			его	полуоси; 2)

координаты фокусов; 3) эксцентриситет; 4) уравнения директрис.

3.2.29. Вычислить площадь четырехугольника, две вершины которого лежат в фокусах эллипса x 2 +5y2 = 20 , две другие совпадают с концами его

малой оси.

3.2.30. Прямая x − y −5 = 0 касается эллипса, фокусы которого находятся в точках F1 (−3;0)и F2 (3;0). Составить уравнение этого эллипса.

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 129 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.03.201523.86 Mб94Raschet_tsepey_postoyannogo_toka_2.doc
#
06.03.20163.73 Mб249ravich_b_m_okladnikov_v_p_i_dr_kompleksnoe_ispolzovanie_syry.doc
#
17.03.20151.15 Mб48razdel1kim.pdf
#
17.03.20151.31 Mб24razdel1UMK.pdf
#
17.03.20151 Mб59razdel2kim.pdf
#
17.03.20151.08 Mб32razdel2UMK.pdf
#
17.03.2015780.33 Кб33razdel3kim.pdf
#
17.03.20151.22 Mб88razdel3UMK.pdf
#
17.03.2015768.02 Кб25razdel4kim.pdf
#
17.03.20151.03 Mб39razdel4UMK.pdf
#
17.03.201569.38 Кб35rechev_kommun.docx