Курс лекций по ТМО_ Абузова Ф[1].Ф

В барботажных ТОА теплообмен происходит при контакте теплоно-

сителей, но они не растворяются друг в друге.

Рис. 8.3. Рекуперативный ТОА

По назначению ТОА:

∙воздухоподогреватели;

∙пароперегреватели;

∙маслоохладители и т.д.

По конструктивным особенностям ТОА:

∙« труба в трубе»;

∙кожухотрубные;

∙аппараты воздушного охлаждения (АВО).

Виды теплового расчёта

ТОА широко распространены в промышленности, особенно в тепло-

снабжении. Для их использования необходимы расчёты при проектирова-

нии и эксплуатации.

При проектировании цель – определение поверхности теплообмена – это конструкторский расчёт.

При эксплуатации и режимных расчётах цель – определение конеч-

ных температур теплоносителей – это поверочный расчёт.

где M1, M2 – массовые расходы горячего и холодного теплоносителя;

73

h1, h2 – удельные массовые энтальпии теплоносителей.

го теплоносителя;

cpm2 t′′2 – средняя удельная изобарная массовая теплоёмкость холод-

t′2

ного теплоносителя.

Если один из теплоносителей – жидкость, а другой – пар.

Написание уравнений может несколько отличаться, суть остаётся:

количество теплоты, внесённое в ТОА горячим теплоносителем, равно ко-

личеству теплоты, воспринятому холодным теплоносителем, за вычетом потерь.

В тепловых расчётах часто пользуются понятием полной теплоёмко-

сти массового расхода:

∙ W1 =M1 cpm1 – расходная массовая теплоёмкость горячего теплоноси-

теля;

∙ W2 =M2 cpm2 – расходная массовая теплоёмкость холодного теплоно-

сителя.

Тогда (8.33) можно записать в виде:

74

при переменных температурах теплоносителей (см. далее).

Формулу (8.36) следует сопоставить с формулой (3.17):

Схемы движения теплоносителей

Вход в ТОА определяется по горячему теплоносителю. Соответст-

венно бывают ТОА:

∙с прямотоком

∙с противотоком

∙с перекрёстным током

∙со смешенным током

∙ с многократно перекрёстным током

75

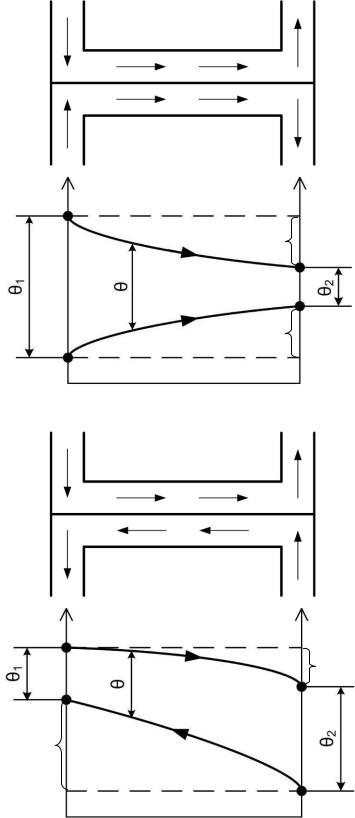
Распределение температур при прямотоке и противотоке

Ниже представлены схемы прямотока и противотока и распределе-

ние температур.

Рис. 8.4. Прямоток (изображён случай, когда W1 ≈ W2 )

Δt1

Δt2

F, L

Рис. 8.5. Противоток (изображён случай, когда W1 >W2 )

76

Средний температурный напор

Для прямотока и противотока средний температурный напор рассчи-

тывается по следующей формуле:

ln θб θм

где θб – больший температурный напор;

θм – меньший температурный напор.

Рис. 8.6. Больший и меньший температурный напор

Для сложных схем движения теплоносителей используют метод Бау-

мана:

77

Рис. 8.7. Эквидистантные кривые изменения температур теплоносителей Средний температурный напор используется в конструкторском рас-

чёте с уравнением теплопередачи для нахождения величины поверхности теплообмена:

где Q – тепловой поток (мощность ТОА или его теплопроизводитель-

ность по холодному теплоносителю).

Расчёт конечных температур теплоносителей

78

где Wmz – приведённая расходная теплоёмкость при противотоке.

Обобщение по видам теплообмена

Лекция 9

2. МЕТОДЫ ТЕОРИИ ТЕПЛОМАССОБМЕНА

2.1. Особенности движения и теплообмена в трубах (физическое содержание табл. 2)

Течение в прямой трубе

Критические значения числа Рейнольдса используются для разгра-

ничения режимов течения среды:

∙ Reкр1 =2000 – разделяет ламинарную и переходную область;

79

∙ Reкр2 =104 – разделяет переходную и турбулентную область.

Таким образом, если:

∙Re <Reкр1 – режим течения ламинарный;

∙Reкр1 <Re <Reкр2 – режим течения переходный;

∙Reкр2 <Re – режим течения турбулентный.

Участок гидродинамической стабилизации

Рис. 9.1. Участок гидродинамической стабилизации На рисунке изображен ламинарный режим течения (вход в трубу с

закруглёнными краями из большого объёма). Течение изотермическое, те-

плофизические свойства постоянны.

Расстояние от входа до сечения, где смыкаются пограничные слои,

называется длиной гидродинамического начального участка или уча-

стка гидродинамической стабилизации.

Если x ≥lн , то течение стабилизированное. Такое течение не зави-

сит от начального распределения скоростей на входе (при x =0 ). Однако распределение скоростей на любом участке при любом x зависит от теп-

лообмена.

Начальный участок наблюдается как при ламинарном, так и при тур-

булентном режиме.

Иногда при Re >Reкр1 в начале трубы – ламинарное движение, а за-

тем турбулентное. Если переходный режим попадает на начальный уча-

80

сток, может наблюдаться перемежаемость режимов. Изменение режима может быть при x >lн , но если Re ≥5 104 , всегда наблюдается турбулент-

ный режим.

На входе в трубу с острой кромкой из большого объёма образуются вихри и ламинарный пограничный слой разрушается.

Для ламинарного течения характерно следующее распределение скоростей поперёк потока:

Средняя скорость при ламинарном течении

Рис. 9.3. Турбулентное течение в трубе

81

Если жидкость малотеплопроводная, то основное термическое сопротивление при теплообмене оказывает ламинарный подслой.

Участок термической стабилизации

Рис. 9.4. Участок термической стабилизации при охлаждении ( to > tc )

При x >lнт (lнт – длина участка тепловой стабилизации) профиль температуры t меняется, т.к. жидкость остывает.

ϑ = t +to

Рис. 9.5. Участок термической стабилизации при нагревании ( to <tc )

Для данной задачи справедливо уравнение:

ски стабильном течении скорость изменения этих величин одинакова.

82