
Курс лекций по ТМО_ Абузова Ф[1].Ф
..pdf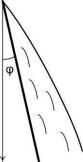
Рис. 7.3. Конденсация пара на наклонной стенке |
|
||||
Средняя температура конденсата: |
|
||||
t |
|
= |
tc +ts |
. |
(7.10) |
ср |
|
||||
|
2 |
|
|
||
|
|
|
|
||
Формулы (7.3) – (7.9) приближенные, они справедливы при следую-
щих допущениях:
1)плёнка течёт ламинарно;
2)силы инерции в плёнке малы по сравнению с силами вязкости и веса;
3)конвективный перенос и теплопроводность вдоль плёнки значительно меньше, чем поперёк;
4)трение пара о конденсат стремится к нулю;
5)температура конденсата на поверхности примерно равна температу-
ре насыщения; 6) теплофизические параметры (ρ , λ, ν) не зависят от температуры
(принимаются при средней температуре конденсата).
Формулы (7.3) – (7.9) справедливы для чистого пара и чистой по-
верхности конденсации.
∙ Перегрев пара.
Перегрев ведёт к возрастанию коэффициента теплоотдачи. Если пар перегрет, то вместо r следует подставлять:
r′= r +q |
пер |
, |
(7.11) |
|
|
|
где qпер – теплота перегрева.
∙ Состояние поверхности.
63

На шероховатой поверхности коэффициент теплоотдачи снижается,
т.к. возрастает толщина плёнки (7.3).
Рис. 7.4. Конденсация пара на шероховатой стенке |
|
∙ Содержание неконденсирующихся газов. |
|
Давление у поверхности: |
|
po = pв +pп , |
(7.12) |
где pв – парциальное давление воздуха; pп – парциальное давление пара.
Содержание неконденсирующихся газов уменьшает коэффициент теплоотдачи, т.к. воздух накапливается у поверхности конденсатной плён-
ки.
Рис. 7.5. Давление и температура вблизи плёнки
∙ Скорость и направление движения пара.
64

А |
Б |
Рис. 7.6. Влияние скорости и направления движения пара на α
В случае А коэффициент теплоотдачи уменьшается (плёнка стано-
вится толще), в случае Б – увеличивается.
∙ Компоновка поверхности.
Применяют конденсатоотводные колпачки для увеличения α.
Рис. 7.7. Конденсатоотводные колпачки
Лекция 8
1.6. Теплообмен излучением в прозрачной среде. Сложный теплообмен
Тепловое излучение – это процесс перехода внутренней энергии в
лучистую и распространение этой энергии в пространстве.
65

Поглощение – это превращение падающей на тело лучистой энергии во внутреннюю.
Передача теплоты, обусловленная взаимным излучением и погло-
щением тел, имеющих разную температуру, называется теплообменом
излучением.
Перенос лучистой энергии рассматривается как с точки зрения элек-
тромагнитной, так и квантовой теории.
Виды излучения |
Длина волны, нм |
|
Космическое |
|
0,05 |
Гамма-излучение |
|
0,05 ÷0,10 |
Рентгеновское |
|
0,10 ÷2,00 |
Ультрафиолетовое |
|
2,00 ÷350 |
Видимое |
|
350 ÷700 |
Тепловое (инфракрасное) |
|
700 ÷4 105 |
Радиоволны |
|
4 105 и выше |
Общий поток лучистой энергии: |
|
|
Eпад = Eпогл +Eотр +Eпропуск |
(8.1) |
|
Если поделить члены правой части на величину Eпад , получим:
∙Епогл = A – коэффициент поглощения;
Епад
∙Еотр = R – коэффициент отражения;
Епад
∙Епропуск = D – коэффициент проницаемости.
Епад
Тогда (8.1) можно записать |
|
A +R +D =1. |
(8.2) |
Если A =1, тело – абсолютно чёрное (~сажа); R =1, тело – абсолют-
но белое (~зеркало); D =1, тело – абсолютно прозрачное (~стекло). В при-
роде нет абсолютно черных, белых и прозрачных тел.
Эти коэффициенты относятся к узкому диапазону длин волн от λ до
λ +dλ . Для разных диапазонов коэффициенты меняются. Аλ, Rλ – моно-
66

хроматичное излучение. Иней и снег в области тепловых волн – практиче-
ски чёрные тела ( A =0,95 ÷0,98 ).
Основные законы теплового излучения
Суммарное количество энергии, излучённое на всех длинах волн в
единицу времени, называется полным потоком теплового излучения Е.
Энергия при определённом значении λ (в узком диапазоне λ) называ-
ется потоком монохроматического излучения Еλ.
Поверхностная плотность потока теплового излучения:
e = |
dE |
. |
(8.3) |
|
|||
|
dF |
|
|
При одинаковой температуре t излучаемая энергия распределяется различно при различных длинах волн λ, поэтому вводят спектральную плотность потока теплового излучения:
i = |
dE |
. |
(8.4) |
λ dλ
∙ Закон Планка При окружающих температурах наибольшее излучение наблюдается
в инфракрасной области.
|
= |
C λ−5 |
|
, |
(8.5) |
||
isλ |
|
1 |
|
|
|||
|
C2 |
|
|
||||
|
|
exp |
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
λ T |
|
|
|
|
где C1 =3,74 10−16 Вт ;
м2
C2 =1,44 10−2 м К .
67

Рис. 8.1. К закону Планка (isλ – для абсолютно чёрного тела, T1 <T2 <T3 )
∙Закон смещения Вина
Сувеличением температуры максимум излучения сдвигается в об-
ласть коротких волн.
|
|
|
|
|
|
|
λmax T = 2,9 |
мм |
. |
(8.6) |
||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
К |
|
||
∙ Закон Стефана-Больцмана: |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
es = σs T4 , |
(8.7) |
||||||||
|
|
|
|
−8 |
|
Вт |
|
|
|
|
|
|
|
|||
где |
σs |
=5,67 10 |
|
– постоянная излучения Стефана-Больцмана. |
||||||||||||
м2 К4 |
||||||||||||||||
|
Иначе закон может быть записан |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
T |
4 |
|
|||||
|
|
|
|
|
|
|
es = сs |
|
|
|
, |
(8.8) |
||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
100 |
|
|
|||||
где |
с |
|
=5,67 |
Вт |
|
– постоянная |
излучения абсолютно |
чёрного тела |
||||||||
s |
м2 К4 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(АЧТ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Поскольку в природе нет абсолютно чёрных тел, то необходимо ис- |
|||||||||||||||
пользовать поверхностную плотность обычного тела. |
|
|||||||||||||||
|
Введём степень черноты |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
ε = |
e |
. |
|
|
|
(8.9) |
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
es
Таким образом:
68
e = ε es . |
|
|
|
(8.10) |
Степень черноты зависит от материала, состояния поверхности и |
||||
температуры тела, ε =0 ÷1. |
|
|
|
|
С учётом (8.7) и (8.8) получаем |
|
|
|
|
|
T |
4 |
|
|
e =ε σs T4 = ε сs |
|
|
. |
(8.11) |
|
||||
|
|
|
|
|
|
100 |
|
|
|
∙ Закон Кирхгофа (следствие)
Абсолютно чёрное тело поглощает и излучает больше всех осталь-
ных тел.
A = |
σ T4 |
= |
σ |
=ε . |
(8.12) |
σs T4 |
|
||||
|
|
σs |
|
||
Теплообмен излучением между реальными телами усложняется тем,
что часть излученной энергии многократно отражается от одной поверхно-
сти к другой, пока полностью не поглотится, поэтому для определения те-
плового потока, являющегося результатом теплообмена излучением, вво-
дится понятие эффективной плотности потока теплового излучения.
Пусть D =0 , A, R ≠0 , тогда для эффективной плотности потока теп-
лового излучения имеем:
e |
эф |
= e +e |
пад |
1−A |
, |
(8.13) |
|
|
( ) |
|
|
где е – собственное излучение;
eпад (1−A) – отраженное излучение; eпад – энергия, падающая на тело извне.
Теплообмен излучением системы тел в прозрачной среде
Рассмотрим теплообмен излучением между телами на практике – те-
плообмен между 2-мя параллельными пластинами.
69

Рис. 8.2. Теплообмен излучением между 2-мя параллельными пластинами
(T1 > T2)
Для первой и второй пластины запишем выражения для эффективно-
го потока теплового излучения:
|
|
|
|
|
|
|
|
|
|
|
E1эфф = Е1 +(1−A1) E2эфф ; |
|
|
|
(8.14) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E = σ |
T4 F ; |
|
|
|
|
|
|
|
|
|
(8.15) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E1эфф = σ1 T14 F +(1−A1) E2эфф ; |
|
|
(8.16) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
E2эфф =σ2 T24 F +(1−A2 ) E1эфф . |
|
|
(8.17) |
|||||||||||||||||||
Подставим (8.17) в (8.16): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
E1эфф = σ1 T14 F +(1−A1) (σ2 T24 F +(1−A2 ) E1эфф). |
(8.18) |
||||||||||||||||||||||||||||
Раскроем скобки в (8.18) и разрешим относительно E1эфф |
|
|
|
|
|||||||||||||||||||||||||||
E1эфф= σ1 T14 F+σ2 T24 F+(1−A2 ) E1эфф−A1 σ2 T24 F−A1 (1−A2 ) E1эфф. |
|||||||||||||||||||||||||||||||
|
|
|
|
E |
|
|
|
= |
σ1 T14 F +σ2 T24 F (1−A1) |
. |
|
|
|
(8.19) |
|||||||||||||||||
|
|
|
|
1эфф |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
A1 +A2 |
−A1 A2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Аналогично |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
σ |
|
T4 F +σ |
T4 F 1−A |
2 ) |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
E |
|
|
|
= |
|
|
2 |
|
2 |
|
1 |
1 |
( |
|
|
|
. |
|
|
(8.20) |
|||||||
|
|
|
|
2 |
эфф |
|
|
|
|
|
A1 +A2 −A1 |
A2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Если T1 >T2 , тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
σ |
T4 F +σ |
|
T4 |
F 1−A |
1) |
|
σ |
|
T4 |
F +σ |
T4 |
F 1−A |
2 ) |
|
||||||||||||
Q = E |
−E |
|
= |
|
|
1 |
|
1 |
|
|
|
|
2 |
2 |
( |
− |
|
2 |
|
2 |
1 |
1 |
( |
|
. |
||||||
2эфф |
|
|
|
|
|
A1 +A2 −A1 A2 |
|
|
|
|
|
|
A1 +A2 |
−A1 A2 |
|
|
|||||||||||||||
1эфф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Получаем
70
Q = |
|
σ |
T4 |
F A |
2 |
−σ |
2 |
T4 |
F A |
1 |
. |
|
(8.21) |
|||||||||||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
A1 +A2 −A1 A2 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
На основе (8.12) можно записать: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
σ =ε σs ; |
|
|
|
|
|
|
|
|
(8.22) |
|||||||||||
|
|
|
|
|
|
|
|
|
σ1 = A1 σs ; |
|
|
|
|
|
|
(8.23) |
||||||||||||||
|
|
|
|
|
|
|
|
|
σ2 = A2 σs . |
|
|
|
|
|
|
(8.24) |
||||||||||||||
Подставим (8.22) – (8.24) в (8.21): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Q = |
ε σ |
s |
T4 F ε |
2 |
−ε |
2 |
σ |
s |
T4 |
F ε |
|
|||||||||||||||||||
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
. |
(8.25) |
||||||||
|
|
|
|
|
|
|
|
|
ε1 +ε2 −ε1 ε2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Поделим числитель и знаменатель (8.25) на ε1 ε2 : |
|
|||||||||||||||||||||||||||||
|
|
|
Q = |
σs F (T14 −T24 ) |
. |
|
|
|
|
|
(8.26) |
|||||||||||||||||||
|
|
|
|
|
1 |
+ |
1 |
−1 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
ε2 |
|
|
ε1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Введём приведённую поверхность (F12) и приведённую степень чер- |
||||||||||||||||||||||||||||||
ноты (ε12): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F12 |
|
|
|
|
=ε12 F12 . |
|
|
|
|
(8.27) |
|||||||||||
|
|
|
|
|
|
1 |
|
+ |
1 |
−1 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
ε2 |
|
|
|
ε1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким методом можно решить задачу теплообмена излучением меж-
ду телом и оболочкой.
F12 ε12 |
= |
|
|
|
|
F1 |
|
|
|
|
. |
|
|
|
|
F |
|
|
1 |
|
|||||
|
1 |
|
|
|
||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
2 |
|
|
|
2 |
|
|
|||
|
|
|
ε |
|
F |
|
|
ε |
|
|
|
|
В случае, если F1 F2 (например, тело и среда):
F12 ε12 =F1 ε1 ; |
|
|
|
|||||
|
|
T1 |
4 |
T2 |
4 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Q =ε cs |
|
|
|
− |
|
|
|
F . |
|
|
|
|
|
|
|
||
|
100 |
|
100 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8.28)
(8.29)
(8.26)
Чаще всего происходит совместный перенос теплоты КТО и излуче-
нием, тогда приблизительно считают αл :
71

αл =0,04 ε12 сs 100Tm 3 ;
Tm = T1 +T2 ; 2
Qл = αл F12 (T1 −T2 );
QΣ = Qл +Q =(αл +α) (t1 −t2 ) F .
(8.27)
(8.28)
(8.29)
(8.30)
1.7. Основы теплового расчёта теплообменных аппаратов
Теплообменный аппарат (ТОА) предназначен для передачи тепла от горячего теплоносителя к холодному.
Краткая классификация ТОА
По принципу действия различают ТОА:
∙ Поверхностные:
o рекуперативные;
oрегенеративные.
∙Контактные:
oсмесительные;
oбарботажные.
∙С внутренним источником теплоты:
oэлектронагреватели;
o реакторы АЭС.
В рекуперативных ТОА оба теплоносителя движутся одновремен-
но, причём они разделены твёрдой стенкой.
В регенеративных ТОА поверхность теплообмена попеременно
омывается то горячим, то холодным теплоносителем.
В смесительных ТОА теплообмен обеспечивается в результате
смешения двух теплоносителей (например, градирня).
72
