
- •Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
- •1. Цели и задачи дисциплины
- •2. Требования к уровню освоения содержания дисциплины
- •3.Трудоемкость дисциплины по видам занятий
- •4. Содержание дисциплины
- •4.1. Разделы дисциплины и виды занятий (в часах)
- •4.2. Содержание разделов
- •I семестр
- •Раздел 1. Элементы векторной алгебры и аналитической геометрии
- •Раздел 2. Введение в математический анализ: функция, теория пределов,
- •Раздел3. Дифференциальное исчисление функции одной переменной
- •Раздел 4. Функции нескольких переменных
- •II семестр Раздел 5 Элементы теории функции комплексного переменного и высшей алгебры
- •Раздел6. Неопределенный интеграл
- •Раздел7. Определенный интеграл
- •Раздел8. Кратные, криволинейные, поверхностные интегралы
- •III семестр
- •Раздел 9. Элементы теории поля
- •Раздел 10. Обыкновенные дифференциальные уравнения
- •5. Перечень практических занятий
- •I семестр
- •II семестр
- •III семестр
- •IV семестр
- •5 Самостоятельная работа студентов (срс)
- •5.3 Примерный перечень тем курсовых проектов (работ).
- •5.4 Примерный перечень тем рефератов.
- •5.5 Самостоятельное изучение тем разделов программы (материалы для самостоятельной работы студентов:умк дисциплины «Математика»).
- •6.Методические указания к самостоятельной работе студентов.
- •6.1.Векторный анализ
- •6.2.Числовые ряды Основные понятия
- •Простейшие свойства сходящихся рядов
- •Остаток ряда
- •Необходимый признак сходимости ряда
- •Положительные ряды
- •I. Признаки сравнения рядов
- •II. Признак Даламбера (в предельной форме)
- •III. Признак Коши (в предельной форме)
- •IV. Интегральный признак Коши
- •Знакопеременные ряды
- •Достаточный признак сходимости знакопеременных рядов
- •Свойства абсолютно сходящихся рядов
- •Функциональные ряды
- •Понятие функционального ряда и его области сходимости
- •Мажорируемость функционального ряда
- •Равномерная сходимость функционального ряда
- •Степенные ряды
- •Область сходимости степенного ряда
- •Нахождение интервала и радиуса сходимости ряда
- •Условия разложения функции в ряд Тейлора
- •Разложение в ряд маклорена некоторых элементарных функций
- •I Разложение функции
- •II Разложение функции
- •III Разложение функции
- •IV Разложение функции
- •V Разложение функции
- •6.3.Комплексные числа
- •Используя правило возведения в степень, получим
- •6.4.Дифференциальные уравнения Основные понятия
- •Уравнения с разделяющимися переменными
- •Однородные уравнения
- •Линейные уравнения
- •Уравнения в полных дифференциалах. Интегрирующий множитель
- •Уравнения Лагранжа и Клеро
- •Дифференциальные уравнения высших порядков, допускающие понижение порядка.
- •Линейные однородные дифференциальные уравнения высших порядков с постоянными коэффициентами
- •Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Системы дифференциальных уравнений
- •6.5.Теория вероятности
- •Оценим значение
- •6.6. Математическая статистика Вариационные ряды
- •Основные формулы
- •Выборочный метод. Общие вопросы.
- •Эмпирическая функция распределения.
- •Оценка генеральной доли признака
- •Элементы проверки статических гипотез
- •Элементы корреляционного анализа Линейная корреляция
- •Основные формулы
- •Построение теоретического закона распределения по опытным данным. Статистическая гипотеза. Понятие о критериях согласия. Критерий 2 Пирсона.
- •7.Контрольные работы
- •7.1 Контрольная работа №5 Векторный анализ
- •Числовые ряды
- •Комплексные переменные
- •Дифференциальные уравнения
- •7.2Котрольная работа №6
- •7.3 Контрольная работа №7
- •7.4 Контрольная работа №8
- •Математическая статистика
- •8. Учебно-методическое обеспечение дисциплины
- •9.Карта обеспеченности студентов учебниками, учебными пособиями, учебно-методическими материалами по дисциплине "Математика".
- •10. Перечень контрольных вопросов
- •Семестр II
- •Семестр III
- •Семестр IV
Комплексные переменные
Задача
14.Найти модуль и аргумент комплексного
числа:

Задача
15. Вычислить

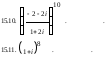
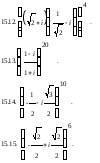
Задача 16. Найти все значения
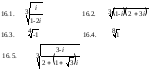
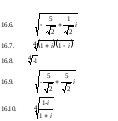

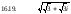
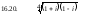
Дифференциальные уравнения
17.1 xy|+1 = ey
17.2
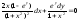
17.3 (1+x2) y||-2xy| = 0
17.4 xy|+1 = ey
17.5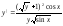
17.6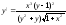
17.7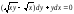
17.8
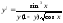
17.9.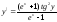
17.10
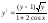
17.11 y|-xy2 = 2xy
17.12 xy|+y = y2, y(1)=0,5
17.13
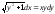
17.14 z| = 10x+z
17.15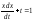
17.16
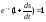
17.17 2x2yy|+y2 = 2
17.18 y| ctgx+y = 2, y(0)=-1
17.19 y| sinx = y lny, y(/2)=1
17.20 x2y| - cos2y = 1
18
.1
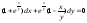
18.2
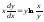
18.3
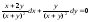
18.4
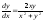
18.5
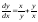
18.6

18.7
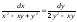
18.8
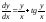
18.9 ydx – (x+y)dy = 0
18.10(y2-3x2)dx – 2xydy = 0
18.11 (x2+2xy-y2)dx+(y2+2xy-x2)dy = 0
18.12
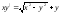
18.13 (y2-2xy)dx+x2dy = 0
18.14 y2+x2y| = xyy|
18.15(x2+y2)y| = 2xy
18.16 xy|-y=x
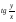
18.17
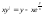
18.18
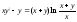
18.19
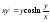
18.20
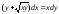
xy|+y = y2 ln x
(2x+1) y| = 4x+2y
x2 dy = (2xy+x2-y)dx
2x (x2+y) dx = dy
xy|+(x+1)y = 3x2e-x
(x+y2)dy = ydx
(sin2y+x ctgy) y| = 1
(2x+y) dy = ydx+4 lny dy
xy dy = (y2+x) dx
y| x3 siny = xy|-2y
(xy+ex) dx-x dy = 0
y = x (y|-x cosx)
(xy|-1) lnx = 2y
2ey-xy| = 1
xy2y| = x2+y3
xy|-2x2
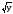 = 4y
= 4y2y|-
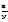 =
=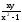
(2x2y lny-x) y| = y
2xy|-6y = -x2
y|+y cosx = sinx cosx
2xy| y|| = y|2-1
y|2+2yy|| = 0
yy||+1=y|2
y||| = 2(y||-1) ctgx
yy|| = y|2-y|3
2yy|| = y2+y|2
y||2+y| = xy||
y||+y|2=2e-y
y||2 = y|2+1
2y| (y||+2) = xy||2
y|2 = (3y-2y|) y||
y|| (2y|+x) = 1
(1-x2) y||+xy| = 2
yy||-2yy| lny = y|2
(y|+2y) y|| = y|2
xy|| = y|+x
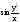
yy||+y = y|2
2yy|3+y|| = 0
y|| (3y+4) – 3y|2 = 0
2xy|y|| = y|2+1
a) y||+y|-2y = 0
b) y||+3y|-4y = e-4x+xe-x
a) y||-2y = 0
b) y||+2y|-3y = x2ex
a) y||-4y|+5y = 0
b) y||-4y|+8y = e2x+sin2x
a) y||+4y = 0
b) y||-2y|+y = 6xex
a) 4y||+4y|+y = 0
b) y||-y = 4shx
a) y|||-3y||+3y|-y = 0
b) y||+4y|+3y=chx
a) y|||-3y|+2y = 0
b) y||+2y|+2y = xe-x
a) y||+4y|+3y = 0
b) y||+y| = 2cosx+ex
a) 2y||-5y|+2y = 0
b) y||+y = 4sinx
a) y||+2y|+10y = 0
b) y||-3y|+2y = x cosx
21.11. a) y||-2y|+y = 0
b) y||+y = 4xex
21.12. a) y|||-6y||+9y| = 0
b) y||+y|-2y = 3xex
a) y||+2y|+y = 0
b) y||-3y|+9y = x cosx
a) y|||-y||-y|+y = 0
b) y||-2y|-3y = e4x
a) y|||+8y||+16y| = 0
b) y||-y = 2ex-x2
a) y||+4y|+3y = 0
b) y||-3y|+2y = sinx
a) y||+y|-2y = 0
b) y||-5y| = 3x2+sin5x
a) y||-3y|+2y = 0
b) y||+y = x sinx
a) y||-5y|+4y = 0
b) y||-9y = e3x cosx
a) y||+2y|-3y = 0
b) y||+4y|+4y = xe2x
