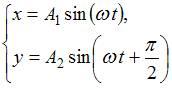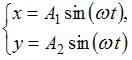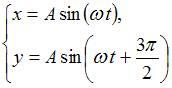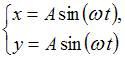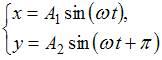вариант 1
.docxВариант 1
ЗАДАНИЕ N 1 Тема: Электростатическое поле в вакууме
Электростатическое
поле создано положительно заряженной
сферой.
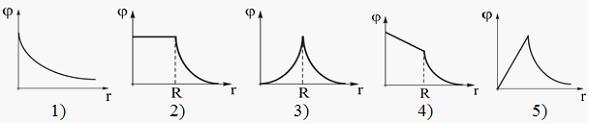 Правильно
отражает зависимость потенциала от
расстояния рисунок …
Правильно
отражает зависимость потенциала от
расстояния рисунок …
|
|
|
2 |
ЗАДАНИЕ N 2 Тема: Законы постоянного тока
На
рисунке представлена зависимость
плотности тока j,
протекающего в проводниках 1 и 2, от
напряженности электрического
поля Е:
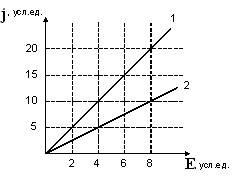 Отношение
удельных сопротивлений r1/r2 этих
проводников равно …
Отношение
удельных сопротивлений r1/r2 этих
проводников равно …
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
4 |
ЗАДАНИЕ N 3 Тема: Магнитостатика
Два
заряда ![]() и
и ![]() движутся
параллельно в одну сторону на
расстоянии r друг
от друга, как показано на рисунке:
движутся
параллельно в одну сторону на
расстоянии r друг
от друга, как показано на рисунке:
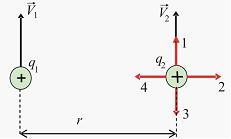 Магнитная
составляющая силы, действующей на второй
заряд со стороны первого заряда, имеет
направление …
Магнитная
составляющая силы, действующей на второй
заряд со стороны первого заряда, имеет
направление …
|
|
|
|
4 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
1 |
Решение:
Индукция
магнитного поля свободно движущегося
заряда равна 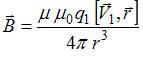 ,
где
,
где ![]() заряд
частицы,
заряд
частицы, ![]() скорость
частицы,
скорость
частицы, ![]() радиус-вектор,
характеризующий положение
заряда
радиус-вектор,
характеризующий положение
заряда ![]() относительно
заряда
относительно
заряда ![]() .
Используя определение векторного
произведения, находим, что вектор
.
Используя определение векторного
произведения, находим, что вектор ![]() в
месте нахождения заряда
в
месте нахождения заряда ![]() направлен
«от нас». Сила Лоренца
направлен
«от нас». Сила Лоренца ![]() по
правилу левой руки имеет направление
4.
по
правилу левой руки имеет направление
4.
ЗАДАНИЕ N 4 Тема: Явление электромагнитной индукции
На
рисунке показана зависимость силы тока
от времени в электрической цепи с
индуктивностью 1 мГн:
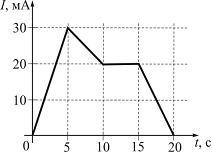 Модуль
среднего значения ЭДС самоиндукции в
интервале от 0 до 5 с (в мкВ)
равен …
Модуль
среднего значения ЭДС самоиндукции в
интервале от 0 до 5 с (в мкВ)
равен …
|
|
|
|
6 |
|
|
|
|
30 |
|
|
|
|
0 |
|
|
|
|
15 |
ЗАДАНИЕ N 5 Тема: Уравнения Максвелла
Утверждение «Переменное электрическое поле, наряду с электрическим током, является источником магнитного поля» раскрывает физический смысл уравнения …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 6 Тема: Электрические и магнитные свойства вещества
На
рисунке представлены графики, отражающие
характер зависимости величины
намагниченности I вещества
(по модулю) от напряженности магнитного
поля Н:
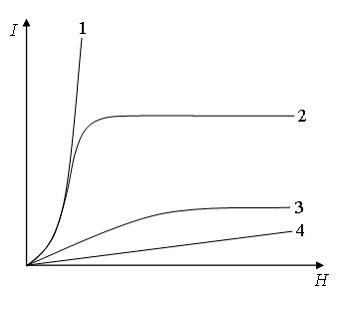 Парамагнетикам
соответствует кривая …
Парамагнетикам
соответствует кривая …
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
4 |
Решение:
К
парамагнетикам относятся вещества,
атомы (молекулы) которых обладают
собственным магнитным моментом. Однако
вследствие теплового движения молекул
их магнитные моменты ориентированы
беспорядочно в отсутствие внешнего
магнитного поля, и намагниченность
вещества в этих условиях равна нулю.
При внесении парамагнетика во внешнее
магнитное поле устанавливается
преимущественная ориентация магнитных
моментов атомов (молекул) в направлении
поля. Таким образом, парамагнетик
намагничивается, создавая собственное
магнитное поле, совпадающее по направлению
с внешним полем и усиливающее его.
Диамагнитный эффект наблюдается и в
парамагнетиках, но он значительно слабее
парамагнитного и поэтому остается
незаметным. Магнитная восприимчивость
парамагнетиков положительна, значительно
меньше единицы и составляет величину ![]() .
В слабом магнитном поле намагниченность
пропорциональна напряженности внешнего
поля. В очень сильном магнитном поле (и
при достаточно низкой температуре)
магнитные моменты всех молекул
располагаются практически параллельно
полю. При этом намагниченность
парамагнетика достигает максимального
значения (но существенно меньшего по
сравнению с ферромагнетиками).
Парамагнетикам соответствует кривая
3.
.
В слабом магнитном поле намагниченность
пропорциональна напряженности внешнего
поля. В очень сильном магнитном поле (и
при достаточно низкой температуре)
магнитные моменты всех молекул
располагаются практически параллельно
полю. При этом намагниченность
парамагнетика достигает максимального
значения (но существенно меньшего по
сравнению с ферромагнетиками).
Парамагнетикам соответствует кривая
3.
ЗАДАНИЕ N 7 Тема: Сложение гармонических колебаний
Складываются
два взаимно перпендикулярных колебания.
Установите соответствие между номером
соответствующей траектории и законами
колебаний точки ![]() вдоль
осей координат
вдоль
осей координат ![]()
![]()
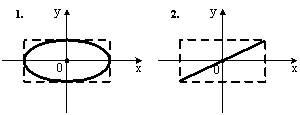
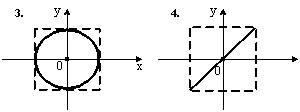
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
Решение:
При
одинаковой частоте складываемых
колебаний уравнение траектории точки
имеет вид: 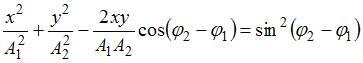 ,
где
,
где ![]() –
разность фаз колебаний. Если разность
фаз
–
разность фаз колебаний. Если разность
фаз ![]() ,
то уравнение преобразуется к виду
,
то уравнение преобразуется к виду 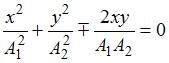 ,
или
,
или 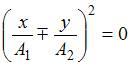 ,
что соответствует уравнению прямой:
,
что соответствует уравнению прямой: 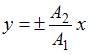 .
Если
.
Если ![]() ,
то
,
то 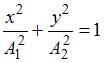 ,
что является уравнением эллипса, причем
если амплитуды равны
,
что является уравнением эллипса, причем
если амплитуды равны ![]() ,
то это будет уравнение окружности.
Если
складываются колебания с циклическими
частотами
,
то это будет уравнение окружности.
Если
складываются колебания с циклическими
частотами ![]() и
и ![]() ,
где
,
где ![]() и
и ![]() целые
числа, точка
целые
числа, точка ![]() описывает
более сложную кривую, которую называют
фигурой Лиссажу. Форма кривой Лиссажу
зависит от соотношения амплитуд, частот
и начальных фаз складываемых колебаний.
описывает
более сложную кривую, которую называют
фигурой Лиссажу. Форма кривой Лиссажу
зависит от соотношения амплитуд, частот
и начальных фаз складываемых колебаний.
ЗАДАНИЕ N 8 Тема: Свободные и вынужденные колебания
На
рисунках изображены зависимости от
времени координаты и ускорения
материальной точки, колеблющейся по
гармоническому закону.
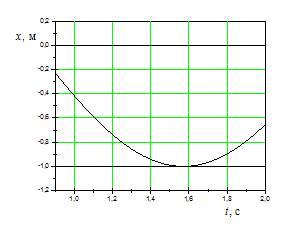
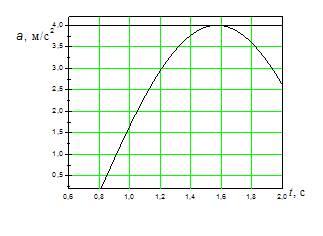 Циклическая
частота колебаний точки равна …
Циклическая
частота колебаний точки равна …
|
|
|
2 |
Решение:
Амплитудное
значение ускорения определяется по
формуле ![]() ,
где
,
где ![]() амплитуда
координаты (максимальное смещение
материальной точки),
амплитуда
координаты (максимальное смещение
материальной точки), ![]() циклическая
частота. Используя графики,
находим:
циклическая
частота. Используя графики,
находим: ![]()
![]() ,
, ![]()
![]() Следовательно,
Следовательно, ![]()
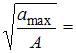
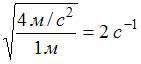 .
.
ЗАДАНИЕ N 9 Тема: Второе начало термодинамики. Энтропия
Если КПД цикла Карно равен 60%, то температура нагревателя больше температуры холодильника в ______ раз(а).
|
|
|
|
2,5 |
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
1,7 |
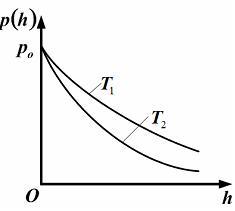
ЗАДАНИЕ N 10 Тема: Распределения Максвелла и Больцмана
Зависимость
давления от высоты для изотермической
атмосферы описывается барометрической
формулой 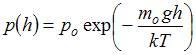 .
Для этой зависимости справедливы
следующие утверждения …
.
Для этой зависимости справедливы
следующие утверждения …
|
|
|
|
зависимость
давления |
|
|
|
|
зависимость |
|
|
|
|
зависимость
давления |
|
|
|
|
с
понижением температуры давление газа
на высоте |
Решение:
Из
барометрической формулы следует, что
зависимость давления от высоты
определяется как температурой газа,
так и массой его молекул. Для одного и
того же газа с повышением температуры
зависимость ![]() становится
все более слабо выраженной, так что
молекулы оказываются распределенными
по высоте почти равномерно. При понижении
температуры давление на высотах, отличных
от нуля, убывает, обращаясь в нуль при
становится
все более слабо выраженной, так что
молекулы оказываются распределенными
по высоте почти равномерно. При понижении
температуры давление на высотах, отличных
от нуля, убывает, обращаясь в нуль при ![]() .
При этом давление
.
При этом давление ![]() определяется
весом всего газа и не меняется при
изменении температуры. Для разных газов
при одинаковой температуре давление
газа с более тяжелыми молекулами убывает
с высотой быстрее, чем для газа с легкими
молекулами.
определяется
весом всего газа и не меняется при
изменении температуры. Для разных газов
при одинаковой температуре давление
газа с более тяжелыми молекулами убывает
с высотой быстрее, чем для газа с легкими
молекулами.
ЗАДАНИЕ N 11 Тема: Средняя энергия молекул
Молярная
теплоемкость идеального газа при
постоянном давлении равна ![]() где
где ![]() –
универсальная газовая постоянная. Число
вращательных степеней свободы молекулы
равно …
–
универсальная газовая постоянная. Число
вращательных степеней свободы молекулы
равно …
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
|
0 |
ЗАДАНИЕ N 12 Тема: Первое начало термодинамики. Работа при изопроцессах
На
рисунке представлена диаграмма
циклического процесса идеального
одноатомного газа:
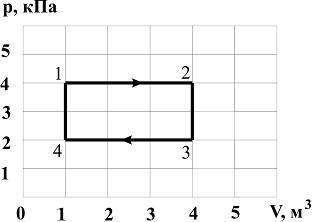 За
цикл газ получает количество теплоты
(в
За
цикл газ получает количество теплоты
(в ![]() ),
равное …
),
равное …
|
|
|
33 |
ЗАДАНИЕ N 13 Тема: Динамика поступательного движения
Тело
массой ![]() движется
равномерно по вогнутому мосту со
скоростью
движется
равномерно по вогнутому мосту со
скоростью ![]() .
В нижней точке сила давления тела на
мост вдвое превосходит силу тяжести.
Радиус кривизны моста (в
.
В нижней точке сила давления тела на
мост вдвое превосходит силу тяжести.
Радиус кривизны моста (в ![]() )
равен …
)
равен …
|
|
|
10 |
ЗАДАНИЕ N 14 Тема: Динамика вращательного движения
Диск
может вращаться вокруг оси, перпендикулярной
плоскости диска и проходящей через его
центр. К нему прикладывают одну из сил
(![]() ,
, ![]() ,
, ![]() или
или ![]() ),
лежащих в плоскости диска и равных по
модулю.
),
лежащих в плоскости диска и равных по
модулю.
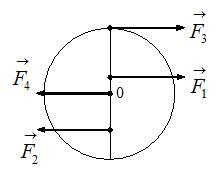 Верным
для угловых ускорений диска является
соотношение …
Верным
для угловых ускорений диска является
соотношение …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Согласно
основному уравнению динамики вращательного
движения твердого тела относительно
неподвижной оси угловое ускорение
равно: 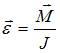 .
Отсюда следует, что угловое ускорение
прямо пропорционально моменту приложенной
к диску силы, который, в свою очередь,
прямо пропорционален величине плеча
силы (при условии равенства модулей
сил). Таким образом,
.
Отсюда следует, что угловое ускорение
прямо пропорционально моменту приложенной
к диску силы, который, в свою очередь,
прямо пропорционален величине плеча
силы (при условии равенства модулей
сил). Таким образом, ![]() ,
, ![]() ,
так как плечо силы
,
так как плечо силы ![]() равно
нулю, и поэтому момент силы
равно
нулю, и поэтому момент силы ![]() равен
нулю.
равен
нулю.
ЗАДАНИЕ N 15 Тема: Работа. Энергия
На
концах невесомого стержня длины l закреплены
два маленьких массивных шарика. Стержень
может вращаться в горизонтальной
плоскости вокруг вертикальной оси,
проходящей через середину стержня.
Стержень раскрутили до угловой скорости ![]() .
Под действием трения стержень остановился,
при этом выделилось 4 Дж теплоты.
.
Под действием трения стержень остановился,
при этом выделилось 4 Дж теплоты.
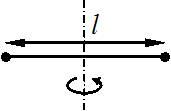 Если
стержень раскрутить до угловой скорости
Если
стержень раскрутить до угловой скорости![]() ,
то при остановке стержня выделится
количество теплоты (в Дж),
равное …
,
то при остановке стержня выделится
количество теплоты (в Дж),
равное …
|
|
|
1 |
Решение:
Согласно
закону сохранения энергии количество
выделившейся теплоты равно убыли полной
механической энергии, в данном случае
– убыли кинетической энергии вращения: 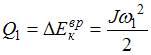 .
Отсюда следует, что при уменьшении
угловой скорости в 2 раза количество
выделившейся теплоты уменьшится в 4
раза, то есть
.
Отсюда следует, что при уменьшении
угловой скорости в 2 раза количество
выделившейся теплоты уменьшится в 4
раза, то есть ![]()
ЗАДАНИЕ N 16 Тема: Элементы специальной теории относительности
Космический
корабль летит со скоростью ![]() (
(![]() скорость
света в вакууме) в системе отсчета,
связанной с некоторой планетой. Один
из космонавтов медленно поворачивает
метровый стержень из положения 1,
перпендикулярного направлению движения
корабля, в положение 2, параллельное
направлению движения. Длина этого
стержня с точки зрения другого космонавта
…
скорость
света в вакууме) в системе отсчета,
связанной с некоторой планетой. Один
из космонавтов медленно поворачивает
метровый стержень из положения 1,
перпендикулярного направлению движения
корабля, в положение 2, параллельное
направлению движения. Длина этого
стержня с точки зрения другого космонавта
…
|
|
|
|
равна 1,0 м при любой его ориентации |
|
|
|
|
изменяется от 1,0 м в положении 1 до 1,67 м в положении 2 |
|
|
|
|
изменяется от 1,0 м в положении 1 до 0,6 м в положении 2 |
|
|
|
|
изменяется от 0,6 м в положении 1 до 1,0 м в положении 2 |
Решение:
Движение
макроскопических тел со скоростями,
соизмеримыми со скоростью света в
вакууме, изучается релятивистской
механикой. Одним из следствий преобразований
Лоренца является так называемое Лоренцево
сокращение длины, состоящее в том, что
линейные размеры тела сокращаются в
направлении движения: 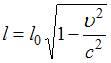 .
Здесь
.
Здесь ![]() –
длина тела в системе отсчета, относительно
которой тело неподвижно;
–
длина тела в системе отсчета, относительно
которой тело неподвижно; ![]() –
длина тела в системе отсчета, относительно
которой тело движется со скоростью
–
длина тела в системе отсчета, относительно
которой тело движется со скоростью ![]() .
При этом поперечные размеры тела не
изменяются. Поскольку с точки зрения
другого космонавта стержень покоится
и в положении 1, и в положении 2, то длина
стержня равна 1,0 м при
любой его ориентации.
.
При этом поперечные размеры тела не
изменяются. Поскольку с точки зрения
другого космонавта стержень покоится
и в положении 1, и в положении 2, то длина
стержня равна 1,0 м при
любой его ориентации.
ЗАДАНИЕ N 17 Тема: Законы сохранения в механике
Сплошной
цилиндр и шар, имеющие одинаковые массы
и радиусы, вкатываются без проскальзывания
с одинаковыми скоростями на горку. Если
трением и сопротивлением воздуха можно
пренебречь, то отношение высот ![]() ,
на которые смогут подняться эти тела,
равно …
,
на которые смогут подняться эти тела,
равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |


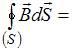 0.
0.