Задание n 1 Тема: Средняя энергия молекул

Если не учитывать колебательные движения в молекуле углекислого газа, то средняя кинетическая энергия молекулы равна …

Решение: Средняя кинетическая энергия молекулы равна: , где – постоянная Больцмана, – термодинамическая температура; – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы: . Для молекулы углекислого газа число степеней свободы поступательного движения , вращательного – , колебательного – , поэтому  Следовательно, средняя кинетическая энергия молекулы равна: .

ЗАДАНИЕ N 2  Тема: Первое начало термодинамики. Работа при изопроцессах

На рисунке представлена диаграмма циклического процесса идеального одноатомного газа: 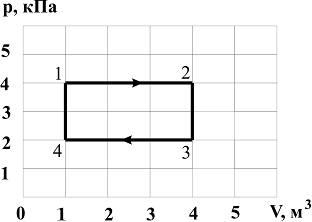За цикл газ получает количество теплоты (в ), равное …

33

Решение: Цикл состоит из изохорного нагревания (4–1), изобарного расширения (1–2), изохорного охлаждения (2–3) и изобарного сжатия (3–4). На первых двух этапах цикла газ получает теплоту. Согласно первому началу термодинамики, количество теплоты, получаемое газом, равно , где – изменение внутренней энергии, – работа газа. Тогда . Таким образом, количество теплоты, получаемое газом за цикл, равно 

ЗАДАНИЕ N 3  Тема: Второе начало термодинамики. Энтропия

В ходе необратимого процесса при поступлении в неизолированную термодинамическую систему тепла для приращения энтропии верным будет соотношение …

Решение: Отношение в обратимом процессе есть полный дифференциал функции состояния системы, называемой энтропией системы: . В изолированных системах энтропия не может убывать при любых, происходящих в ней процессах: . Знак равенства относится к обратимым процессам, а знак «больше» – к необратимым процессам. Если в неизолированную систему поступает тепло и происходит необратимый процесс, то энтропия возрастает за счет не только полученного тепла, но и необратимости процесса: .

Задание n 4 Тема: Распределения Максвелла и Больцмана

На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где – доля молекул, скорости которых заключены в интервале скоростей от до в расчете на единицу этого интервала: Для этой функции верными являются утверждения …

			положение максимума кривой зависит не только от температуры, но и от природы газа (его молярной массы)
			при увеличении числа молекул площадь под кривой не изменяется
			с ростом температуры газа значение максимума функции увеличивается
			для газа с бόльшей молярной массой (при той же температуре) максимум функции расположен в области бόльших скоростей

Решение: Из определения функции распределения Максвелла следует, что выражение определяет долю молекул, скорости которых заключены в интервале скоростей от до (на графике это – площадь заштрихованной полоски). Тогда площадь под кривой равна и не изменяется при изменении температуры и числа молекул газа. Из формулы наиболее вероятной скорости (при которой функция максимальна) следует, чтопрямо пропорциональна и обратно пропорциональна , где и – температура и молярная масса газа соответственно.

ЗАДАНИЕ N 5  Тема: Электростатическое поле в вакууме

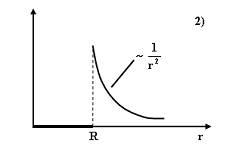
На рисунках представлены графики зависимости напряженности поля для различных распределений заряда: 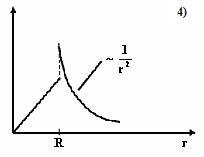График зависимости для шара радиуса R, равномерно заряженного по объему, показан на рисунке …

1

ЗАДАНИЕ N 6  Тема: Законы постоянного тока

На рисунке представлена зависимость плотности тока j, протекающего в проводниках 1 и 2, от напряженности электрического поля Е: 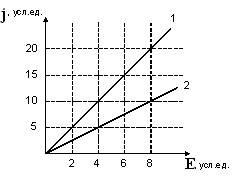Отношение удельных сопротивлений r₁/r₂ этих проводников равно …

			2
			4

ЗАДАНИЕ N 7  Тема: Магнитостатика

Рамка с током с магнитным дипольным моментом , направление которого указано на рисунке, находится в однородном магнитном поле: Момент сил, действующих на магнитный диполь, направлен …

			перпендикулярно плоскости рисунка к нам
			перпендикулярно плоскости рисунка от нас
			по направлению вектора магнитной индукции
			противоположно вектору магнитной индукции