rgr1_-_7_variant

_{Правильность заполнения таблицы проверяем тождеством}

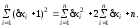
_{406=480-54*2+34}

Выборочное среднее отклонение x_m в выборках малого объема и в объединенной выборке вычисляют по формуле:

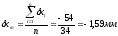
Выборочное среднее квадратическое отклонение S_x в выборках малого объема n  30 единицам и в объединенной выборке вычисляют по формуле:

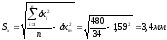
3. Результаты вычислений статистических характеристик по всем выборкам приведены в табл.

Таблица 3. Результаты вычислений статистических характеристик по всем выборкам

№ п\п	Месяц, год	n	dxm, мм	Sx, мм
1	01.2012	34	-0,71	2,88
2	02.2012	34	-1,03	3,08
3	03.2012	34	-0,85	2,98
4	04.2012	34	-1,85	3,08
5	05.2012	34	-1,59	3,40
		Σn=170	Σdxm,= -6,03	Σ Sx =15,42

3. Из действительных отклонений во всех выборках выбираем наибольшее dx_jmax = +4 мм и наименьшее dx_jmin = -6 мм значения.

Поле рассеяния между ними разделим на интервалы шагом

.

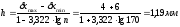Округляем расстояние h до целого значения: h=1 мм.

Тогда количество интервалов расстоянием в 1 мм будет равно 10 с границами, равными -6; -5; -4; -3; -2; -1; 0; 1; 2; 3; 4 мм.

Рассчитаем центры интервалов и выразим их целыми числами. Определим частоты попадания результатов измерений в каждый интервал.

Таблица 4. Результаты вычислений статистических характеристик по всем выборкам

Интервал, мм	Частота появления действительных отклонений fj	Центр интервала, мм
-6…-5	14	-5,5
-5…-4	18	-4,5
-4…-3	18	-3,5
-3…-2	14	-2,5
-2…-1	22	-1,5
-1…0	27	-0,5
0…1	16	0,5
1…2	14	1,5
2…3	10	2,5
3…4	17	3,5

Заносим полученные результаты в графу 2 табл. 5 и строим гистограмму действительных отклонений результатов измерений (табл.5).

Распределим действительные отклонения dxj из всех выборок по интервалам, после чего подсчитаем количество отклонений в каждом интервале (частоты). Далее строим гистограмму и выполняем все промежуточные вычисления в таблице. Правильность заполнения таблицы проверяем тождеством:

;

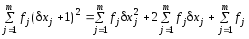1250,5=1458,5-2*189+170

Характеристики dxm и Sx вычисляем по формулам:

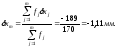
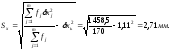
Далее вычисляем значения, соответствующие предельным отклонениям

dxm + 3Sx = 7,02мм;

dxm - 3Sx = -9,24 мм.

Значения отклонений, вышедшие за пределы, ограниченные вычисленными значениями отсутствуют. Это означает, грубых погрешностей, которых необходимо исключить из объединенной выборки, нет. Поэтому в двух последних графах табл. 4 значения сумм и не меняются. Характеристики dxm и Sx также не меняются.

4. Для построения на чертеже гистограммы кривой нормального распределения вычисляем координаты точек кривой - отклонения  и соответствующие им частоты f (табл. 5).

Таблица 5

Отклонения  и соответствующие им частоты f

1=dxm=-1,11 мм
2=dxm + Sx = -1,11 + 2,71 = 1,59 мм 3=dxm - Sx = -1,11 – 2,71 = -3,82 мм
4=dxm + 2Sx = -1,11 + 5,42 = 4,31 мм 5=dxm - 2Sx = -1,11 -5,42 = -6,53 мм
6=dxm + 3Sx = -1,11 + 8,13 = 7,02 мм 7=dxm - 3Sx = -1,11 – 8,13 = -9,24 мм

По полученным координатам  и f на гистограмме определим характерные точки, по которым далее построим теоретическую кривую нормального распределения.

Очертания гистограммы ( табл.5.1)

практически можно считать совпадающими с кривой нормального распределения.

Для завершения проверки по гистограмме были суммированы частоты fj по интервалам, расположенным за границами dxm  tSx при t = 2,0; 2,4; 3,0 и определены соответствующие им суммы частостей.

Сравнение сумм частостей в табл. 6 с допустимыми значениями в табл. 5 показывает, что исследуемое распределение можно считать приближающимся к нормальному.

Таблица 6.

Сравнение сумм частостей с допустимыми значениями

Границы dxm  tSx	Сумма частот за границами	Сумма частостей	Допустимые суммы частостей по табл. 5
t = 3,0; -1,118,13 мм	0	<	5,55
t = 2,4; -1,115,04 мм	0	<	8,60
t = 2,0; -1,115,42 мм	0	<	12,50

5. Для проверки стабильности характеристики Sx из табл. 2 выбираем наибольшее и наименьшее значения Sx max = 3,40 мм и Sx min = 2,88 мм и вычисляем характеристику

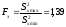
Характеристика Sx в серии выборок стабильна, так как Fэ =1,39 <1.50.

Для проверки стабильности характеристики dxm из табл. 2 выбираем наибольшее и наименьшее значения dxm max =-0,71 мм и dxm min = -1,85 мм, соответствующие им значения Sx1 = 3,08 мм и Sx2 = 2,88, и вычисляем характеристика

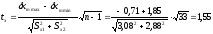
Характеристика dxm в серии выборок стабильна, так как tэ = 1.55 < 2.

6. На основании проверки технологический процесс изготовления панелей по параметру "длина панелей" можно считать статистически однородным.

Так как систематическая погрешность, равная найденному выборочному среднему отклонению dx_m=2.82 мм, превышает значение 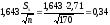мм, то в соответствии с п.2 она должна быть устранена регулированием внутренних размеров форм.

7. Для определения класса точности по длине панелей определяем значение

2 tSx = 22,12,71=11,38 мм.

Значение t = 2,1 примем для приемочного уровня дефектности AQL = 4,0 %.

В соответствии с табл.9 ближайшее большее значение допуска для интервала номинальных размеров от 16000 до 25000 мм (L=19000 мм) равно 12мм, что соответствует 4-му классу точности.

По формуле вычисляем значение

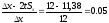
Можно сделать вывод, что запас прочности отсутствует , так как 0,14> 0,05.

Вывод:

По характеристиками tэ и Fэ стабильные..

По совпадениям гистограммы с кривой нормального распределения (метод стратификации) в моей гистограмме 3 пика. Это означает , что данные брались из разных источников ( смен и т.д)., На основании проверки технологический процесс изготовления панелей по параметру «длина панелей» можно считать статически неоднородным.

14
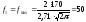
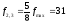
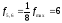
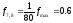
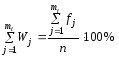
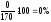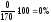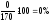