Laboratornaya_rabota_7

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ

КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Отчет

По практическим (лабораторным) работам

Лабораторная работа №7

Выполнили студенты группы ФП-31м:

Гуляев Р.С. и Смирнова Д.А.

Принял:Кушнир Д.В.

каф. ЗСС

Санкт-Петербург

2023

Часть 1.Протокол Диффи-Хелмана

Выбираем простое число «p»

P=241

Выбрать параметр "a":

a=200

Выбрать "секретные параметры" за каждого из пользователей: x_A и x_B

x_A=40

x_B=100

Вычислить открытые параметры

Вычислить итоговый ключ пользователей A и B:

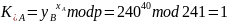
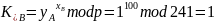
Ключи K_A и K_B равны.

Часть 2. Схема распределения ключей Блома.

Доверенный центр выбирает размер конечного поля и секретную матрицу:

p=25

=

=

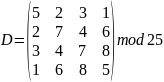
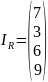
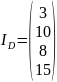
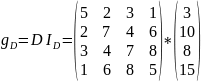Вычисление общего секретного ключа

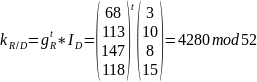
Итог - одинаковый ключ у пользователей А и В.

Часть 3. Протокол Жиро

Вариант 3

Выбирает простые числа p = 43 и q = 92

Вычисляет n=43*92=3956

Вычисляет Fi(n)=(43-1) * (92-1)=3822

Выбирает eЦ=289, такое, что НОД (eЦ, Fi(n)) =1

Вычисляет dЦ=529, такие, что (eЦ * dЦ)=1 mod Fi(n)

Выбираем число g = 63

Создаются идентификаторы пользователей IA, IB

Пользователь А. I_A=97

d_A=201

Пользователь B. I_B=38

d_B=165

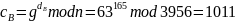
Центр вычисляет:

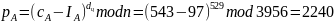
Пользователь А:

Выбирает секрет e_A= 72

Вычисляет s_A=g^(e_A) mod n=

Пересылает I_A, p_A, s_A пользователю B

Пользователь B:

Выбирает секрет e_B = 50

Вычисляет s_B=g^(e_B) mod n=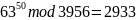

Пересылает I_B, p_B, s_B пользователю A

Пользователь А:

Вычисляет

k=s_B^( d_A) * (p_B^e_Ц+I_B) ^ e_A mod n =

Пользователь B:

Вычисляет

k=s_A^(d_B) * (p_A^e_Ц+I_A) ^e_B mod n =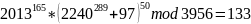

Итоговые ключи пользователей A и B совпадают.