Лабораторная 3 Excel / Отчет_Защита_ЛБ_3_Васильев_Л_5А47
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего образования «Национальный исследовательский Томский политехнический университет» |
Подразделение: Инженерная школа энергетики (ИШЭ)
Направление: 13.03.02 Электроэнергетика и электротехника
Отделение: Электроэнергетики и электротехники (ОЭЭ)
Защита лабораторной работы №3
Вариант - 14
По дисциплине: «Программные средства профессиональной деятельности»
Исполнитель:
|
|
||||
студент группы |
5А47 |
|
Васильев Леонид Максимович |
|
03.05.2025 |
|
|
|
____________________________ |
|
|
|
|
|
(Подпись) |
|
|
Руководитель:
|
|
||||
Доцент ОЭЭ ИШЭ |
к.т.н. |
|
Воронина Наталья Алексеевна |
|
|
|
|
____________________________ |
|
|
|
|
|
|
(Подпись) |
|
|
Томск - 2025 г
Цель работы: Произвести расчет электрической цепи постоянного тока методом Крамера с использованием программного пакета Excel, смоделировать схему в Multisim. Осуществить числовой анализ расчетных и измерительных данных.
Смоделируем заданную схему в Multisim. С помощью измерительных приборов амперметр и вольтметр определим показания падения напряжения и силы тока на каждом участке цепи рис. 1.
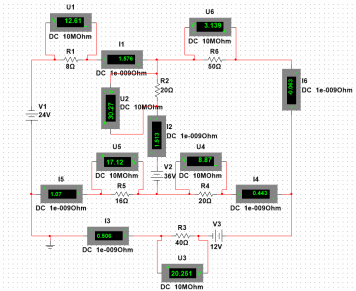
Рис. 1 Смоделированная схема в Multisim
Используя метод Крамера для вычисления токов, необходимо составить уравнения по законам Кирхгофа рис. 2, по данным уравнениям создать две матрица рис. 3.
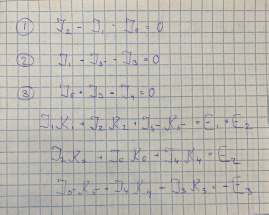
Рис. 2 Уравнения по 1 и 2 законам Кирхгофа
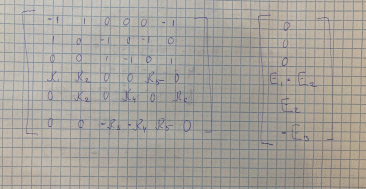
Рис. 3 Основная матрица и матрица правой части
Задаем исходные данные сопротивлений и ЭДС в Excel табл. 1.
Вар. |
R1 (Ом) |
R2 (Ом) |
R3 (Ом) |
R4 (Ом) |
R5 (Ом) |
R6 (Ом) |
E1 (В) |
E2 (В) |
E3 (В) |
14 |
8 |
20 |
40 |
20 |
16 |
50 |
24 |
36 |
12 |
Таблица 1. Исходные данные
Записываем основную матрицу А табл. 2 и рассчитываем определитель для основной матрицы с помощью команды =МОПРЕД в командной строке табл. 3.
Таблица 2. Основная матрица
А= |
-1 |
1 |
0 |
0 |
0 |
-1 |
1 |
0 |
-1 |
0 |
-1 |
0 |
|
0 |
0 |
1 |
-1 |
0 |
1 |
|
8 |
20 |
0 |
0 |
16 |
0 |
|
0 |
20 |
0 |
20 |
0 |
50 |
|
0 |
0 |
-40 |
-20 |
16 |
0 |
А= |
217120 |
Записываем дополнительные матрицы, меняя столбцы основной матрицы на матрицу правой части табл. 4,6,8,10,12,14. Рассчитываем их определители с помощью команды =МОПРЕД в командной строке табл. 5,7,9,11,13,15.
Таблица 4. Дополнительная матрица 1
0 |
1 |
0 |
0 |
0 |
-1 |
0 |
0 |
-1 |
0 |
-1 |
0 |
0 |
0 |
1 |
-1 |
0 |
1 |
60 |
20 |
0 |
0 |
16 |
0 |
36 |
20 |
0 |
20 |
0 |
50 |
-12 |
0 |
-40 |
-20 |
16 |
0 |
А1= |
342240 |
Таблица 5. Определитель матрицы 1
-1 |
0 |
0 |
0 |
0 |
-1 |
1 |
0 |
-1 |
0 |
-1 |
0 |
0 |
0 |
1 |
-1 |
0 |
1 |
8 |
60 |
0 |
0 |
16 |
0 |
0 |
36 |
0 |
20 |
0 |
50 |
0 |
-12 |
-40 |
-20 |
16 |
0 |
Таблица 6. Дополнительная матрица 2
А2= |
328608 |
Таблица 7. Определитель матрицы 2
-1 |
1 |
0 |
0 |
0 |
-1 |
1 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
-1 |
0 |
1 |
8 |
20 |
60 |
0 |
16 |
0 |
0 |
20 |
36 |
20 |
0 |
50 |
0 |
0 |
-12 |
-20 |
16 |
0 |
Таблица 8. Дополнительная матрица 3
А3= |
109920 |
Таблица 9. Определитель матрицы 3
-1 |
1 |
0 |
0 |
0 |
-1 |
1 |
0 |
-1 |
0 |
-1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
8 |
20 |
0 |
60 |
16 |
0 |
0 |
20 |
0 |
36 |
0 |
50 |
0 |
0 |
-40 |
-12 |
16 |
0 |
Таблица 10. Дополнительная матрица 4
Таблица 11. Определитель матрицы 4
А4= |
96288 |
Таблица 12. Дополнительная матрица 5
-1 |
1 |
0 |
0 |
0 |
-1 |
1 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
1 |
-1 |
0 |
1 |
8 |
20 |
0 |
0 |
60 |
0 |
0 |
20 |
0 |
20 |
36 |
50 |
0 |
0 |
-40 |
-20 |
-12 |
0 |
Таблица 13. Определитель матрицы 5
А5= |
232320 |
-1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
-1 |
0 |
-1 |
0 |
0 |
0 |
1 |
-1 |
0 |
0 |
8 |
20 |
0 |
0 |
16 |
60 |
0 |
20 |
0 |
20 |
0 |
36 |
0 |
0 |
-40 |
-20 |
16 |
-12 |
Таблица 14. Дополнительная матрица 6
Таблица 15. Определитель матрицы 6
А6= |
-13632 |
Используя формулу для вычисления по
методу Крамера рис. 4 находим токи табл.
16, далее по закону Ома рассчитываем
напряжения табл. 17.
Рис. 4 Формула для вычисления токов по методу Крамера
I1= |
1,576271 |
I2= |
1,513486 |
I3= |
0,506264 |
I4= |
0,443478 |
I5= |
1,070007 |
I6= |
-0,06279 |
Таблица 16. Вычисленные токи по методу Крамера
U1= |
12,61017 |
U2= |
30,26971 |
U3= |
20,25055 |
U4= |
8,869565 |
U5= |
17,12012 |
U6= |
-3,13928 |
Таблица 17. Вычисленные напряжения по закону Ома
Для сравнения токов и напряжений по расчетам из Excel и измерениям Multisim создадим сравнительную таблицу.
|
I1, (А) |
I2, (А) |
I3, (А) |
I4, (А) |
I5, (А) |
I6, (А) |
U1, (В) |
U2, (В) |
U3, (В) |
U4, (В) |
U5, (В) |
U6, (В) |
Multisim |
1.576 |
1.513 |
0.506 |
0.443 |
1.07 |
-0.063 |
12.61 |
30.27 |
20.251 |
8.87 |
17.12 |
-3.139 |
Excel |
1,576271 |
1,513486 |
0,506264 |
0,443478 |
1,070007 |
-0,06279 |
12,61017 |
30,26971 |
20,25055 |
8,869565 |
17,12012 |
-3,13928 |
Таблица 18. Сравнительная таблица токов и напряжений
Вывод: С помощью программного пакета EWB (Multisim) смоделировали исходную схему, произвели измерительные расчеты при помощи амперметра и вольтметра на каждом участке цепи. Далее рассчитали токи по методу Крамера используя возможности командой строки вычислений программного пакета Excel. Далее занесли данные вычислений в сравнительную таблицу, по которой можно осуществить числовой анализ данных. Анализ числовых данных показывает, практически точные совпадения токов и напряжений до тысячных измерительных данных из Multisim и расчетных данных из Excel. Например: I1 = 1.576 [A], и в Excel I1 = 1.576271 [A], или в Multisim I3 = 0,506 [A], и в Excel I3 = 0,506264 [A]. Также и с напряжением в Multisim U1 = 12.61 [В], и в Excel U1 = 12.61017 [В], или в Multisim U5 = 17,12 [В], и в Excel U5 = 17,12012 [В].