Лабораторочки / 5 / 5
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ТОР
отчет
по лабораторной работе №5
по дисциплине «Техническая электродинамика»
Тема: Волны в коаксиальной линии при произвольной нагрузке
Вариант 4
Студенты гр. фыв |
|
фыв |
фыв |
||
Преподаватель |
|
фыв |
Санкт-Петербург
фыв
Цель работы: исследование параметров отрезков коаксиальной линии при произвольной нагрузке в программе Microwave Office.
Обработка результатов:
Номер варианта |
f0, ГГц |
Θ0, градусы |
Металл |
tg δ |
D, мм |
4 |
2 |
180 |
Серебро |
0.001 |
2 |
Таблица 1 — Параметры варианта 3
Расчёт параметров коаксиальной линии
1.1
Рассчитаем длину волны в линии на рабочей
частоте с учетом диэлектрического
заполнения:
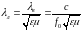 ;
;
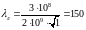 мм.
мм.
Здесь
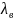 – длина волны в вакууме,
– длина волны в вакууме,
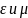 – параметры среды относительно вакуума,
с – скорость света в вакууме, f0
– частота (см.табл.1).
– параметры среды относительно вакуума,
с – скорость света в вакууме, f0
– частота (см.табл.1).
1.2 Рассчитаем погонные емкость С и индуктивность L, проверим результаты расчётом волнового сопротивления
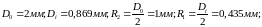
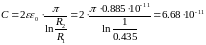 Ф;
Ф;
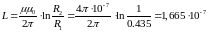 Гн;
Гн;
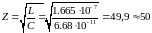 Ом.
Ом.
Полученное сопротивление совпадает с заданным, значит расчёт выполнен верно
1.3 Рассчитаем все представленные в TXLine параметры коаксиальной линии
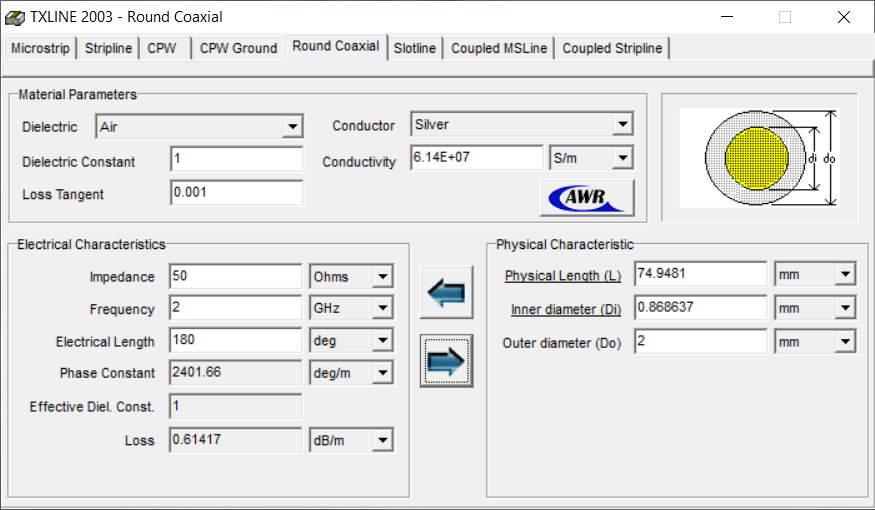
Рисунок 1 — Расчётные параметры коаксиальной линии
1.4 Найдем зависимость погонного затухания от частоты в коаксиальной линии
f, ГГц |
1 |
2 |
4 |
6 |
8 |
10 |
loss |
0,39 |
0,61 |
0,97 |
1,29 |
1,59 |
1,87 |
Таблица 2 — Зависимость погонного затухания от частоты
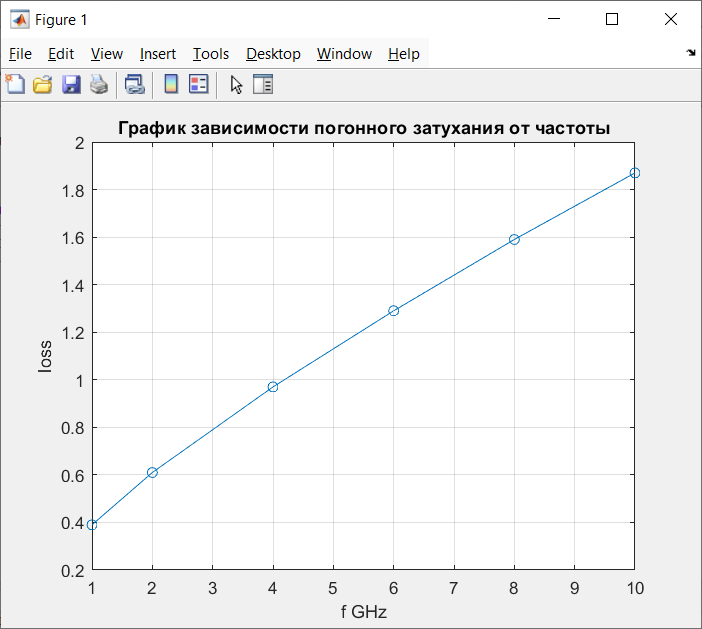
Рисунок 2 — График зависимости погонного затухания от частоты
Расчёт входных характеристик отрезка коаксиальной линии
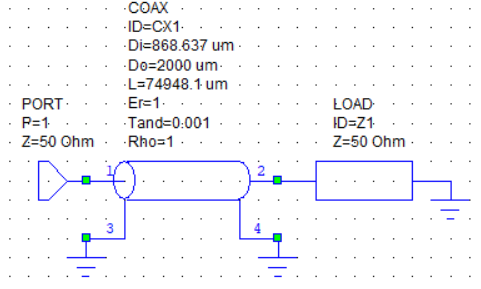
Рисунок 3 — Исследуемая схема
2.1 Рассчитаем значения модуля входного коэффициента отражения и КСВ
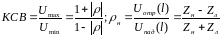 ;
Zл
= 50 Ом.
;
Zл
= 50 Ом.
Zн, Ом |
0 |
25 |
50 |
100 |
50000 |
|
-1 |
-0,333 |
0 |
0,333 |
0,998 |
|
∞ |
2 |
1 |
2 |
1000 |
Таблица 3 — Значения модуля коэффициента отражения и КСВ в зависимости от нагрузки
2.2 Построим семейства графиков зависимостей вещественной и мнимой частей входного сопротивления отрезка коаксиала с различными нагрузками
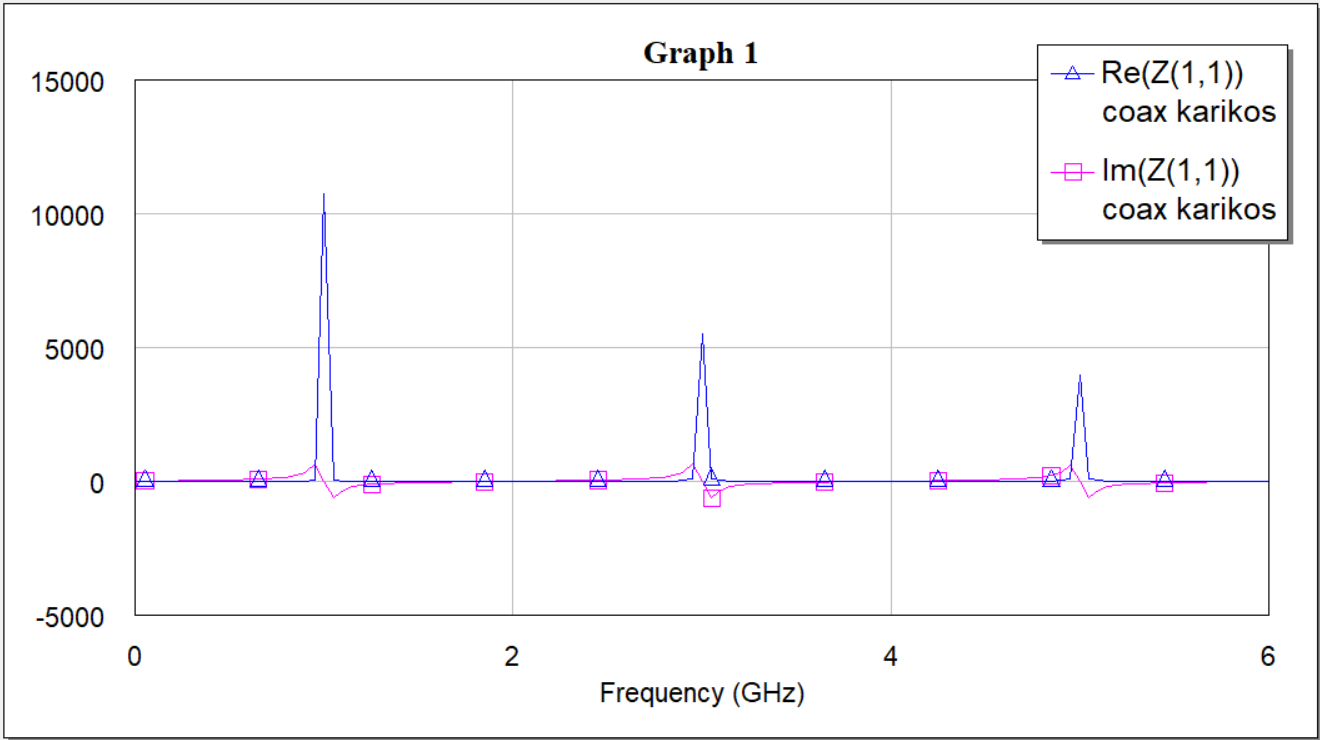
Рисунок 4 — График зависимости вещественной и мнимой частей входного сопротивления от частоты (R=0)
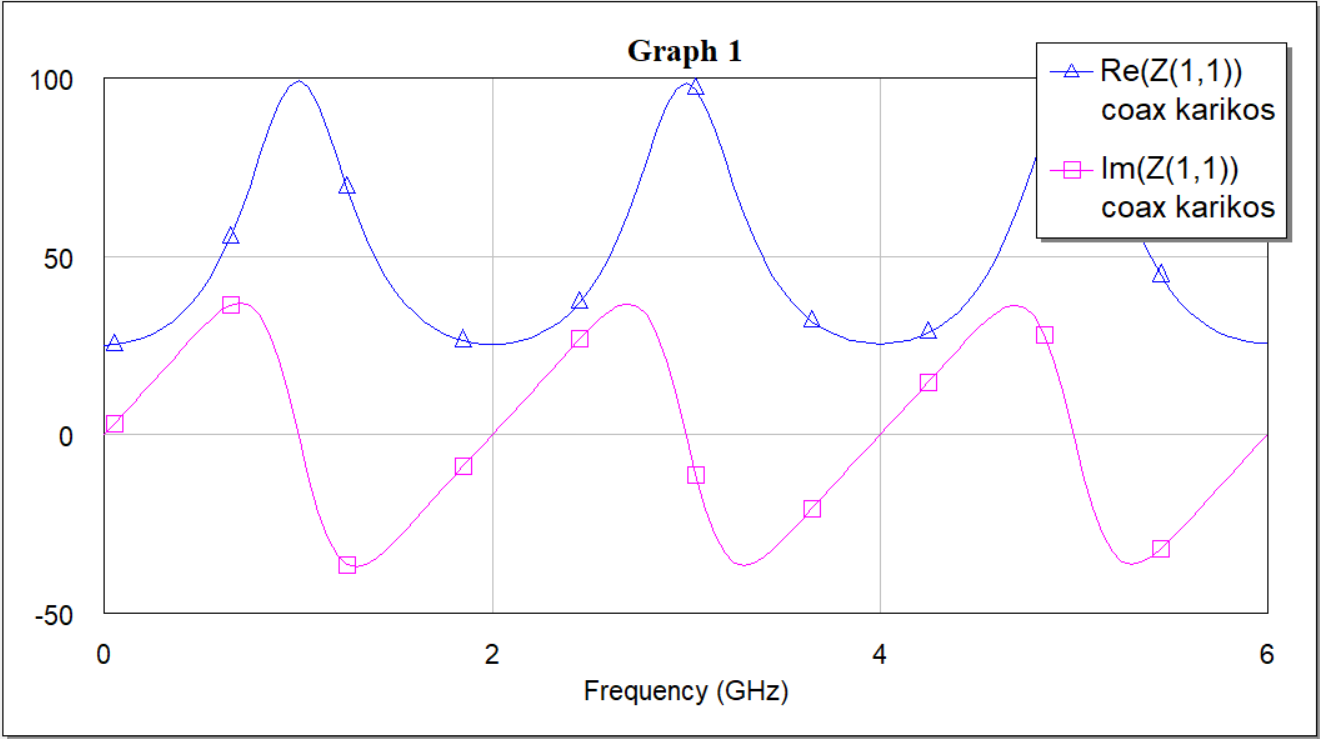
Рисунок 5 — График зависимости вещественной и мнимой частей входного сопротивления от частоты (R=25 Ом)
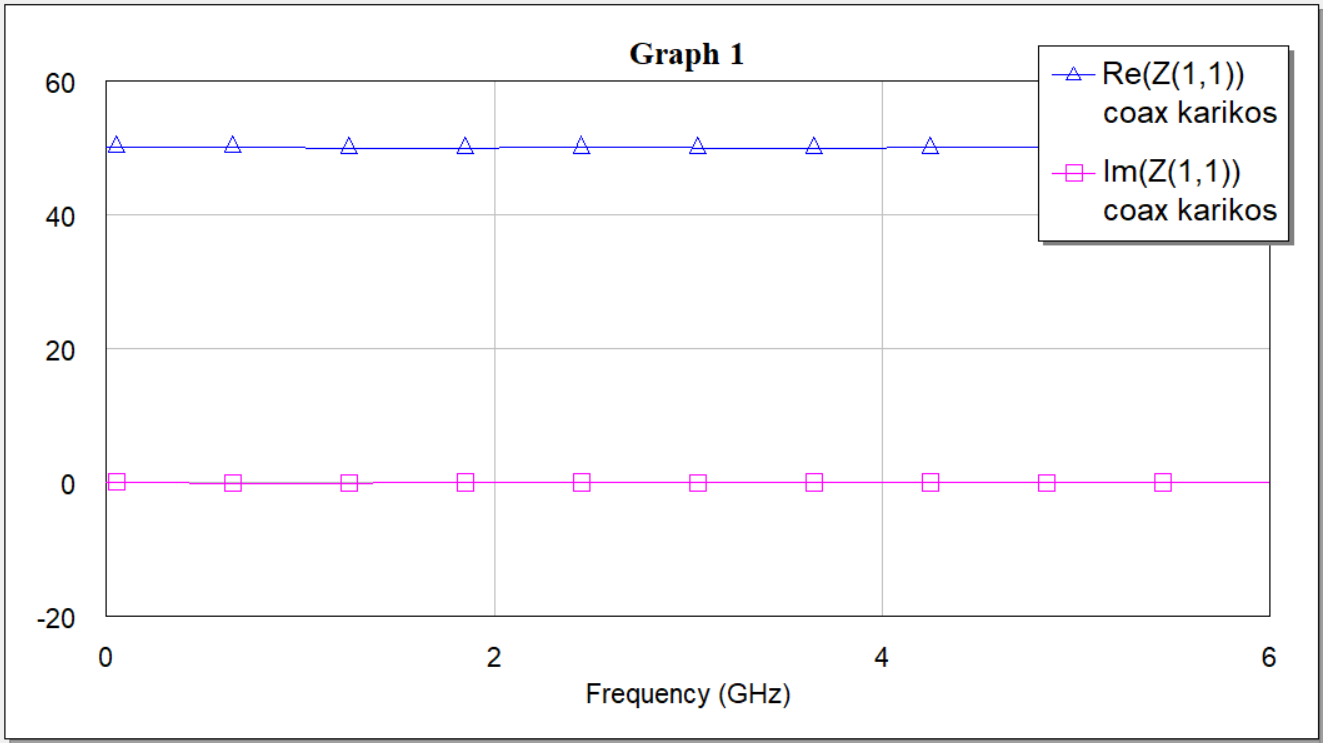
Рисунок 6 — График зависимости вещественной и мнимой частей входного сопротивления от частоты (R=50 Ом)
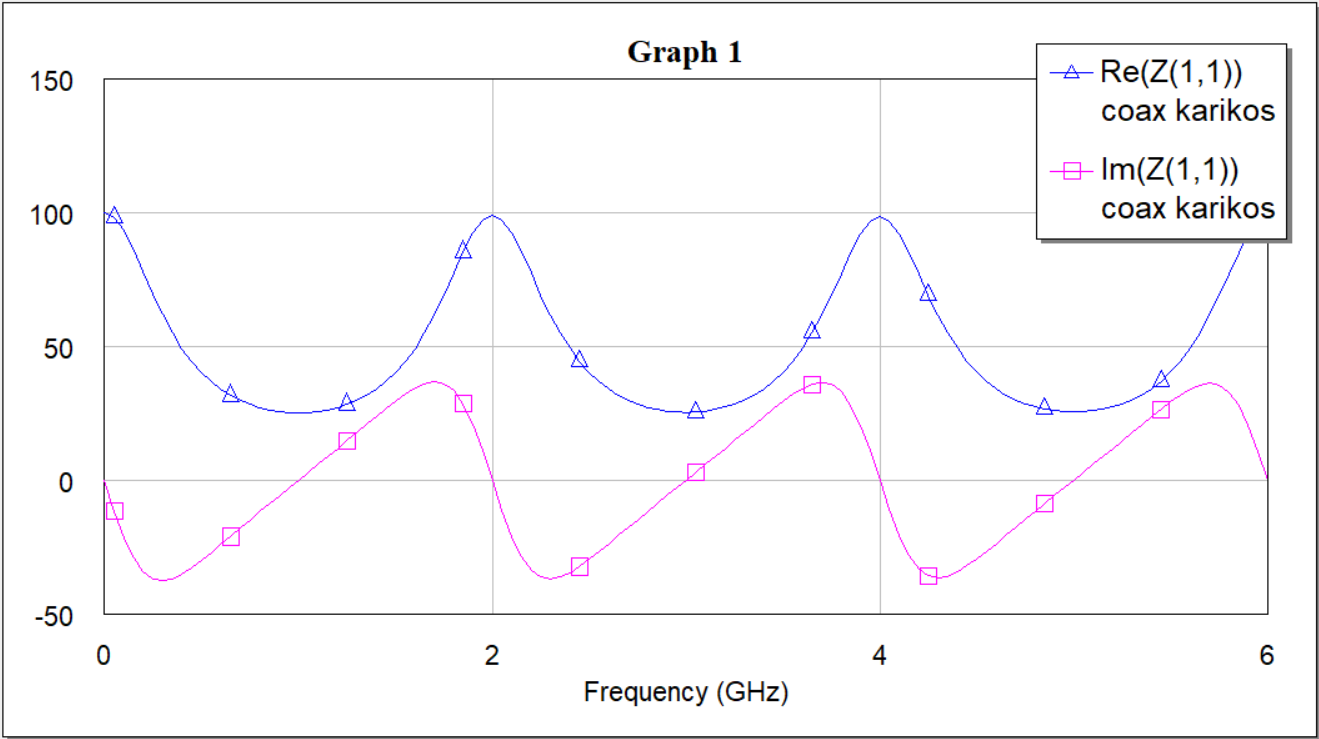
Рисунок 7 — График зависимости вещественной и мнимой частей входного сопротивления от частоты (R=100 Ом)
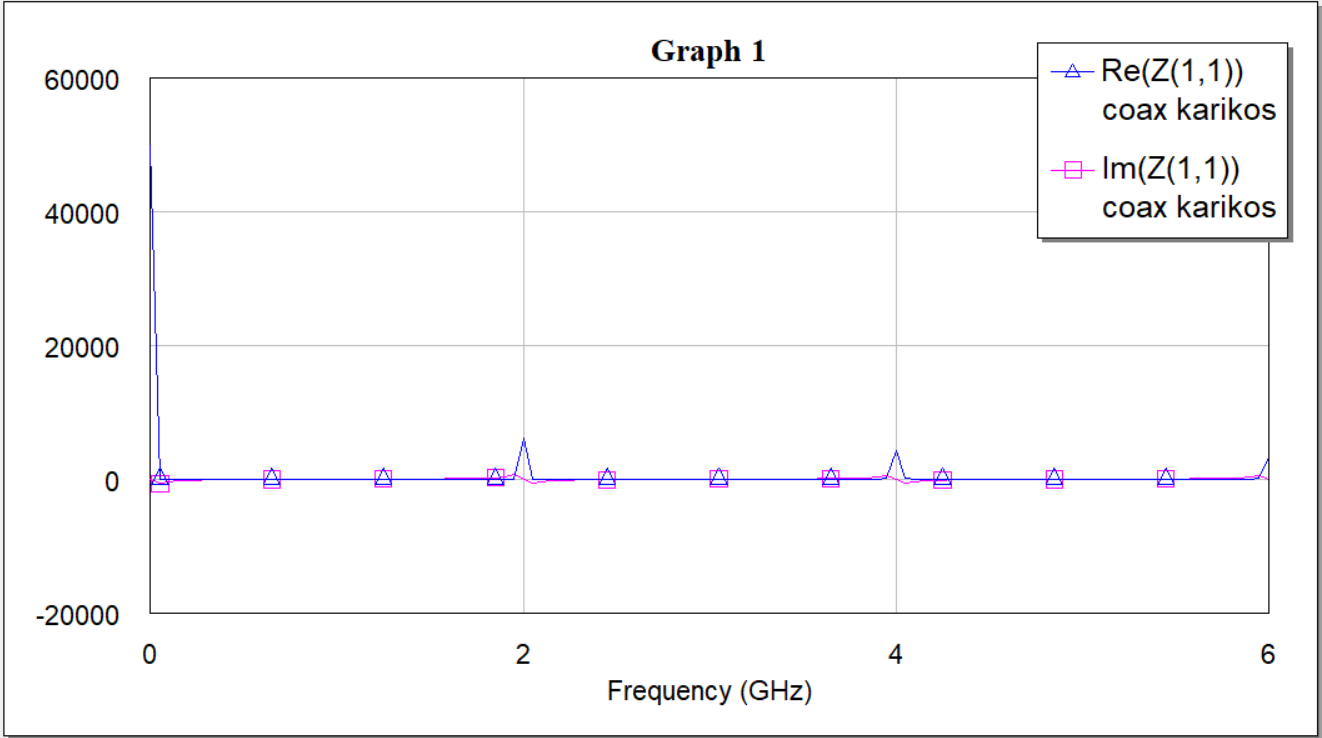
Рисунок 8 — График зависимости вещественной и мнимой частей входного сопротивления от частоты (R=50 кОм)
2.3 На эскизе круговой диаграммы отобразим те же характеристики в полосе частот
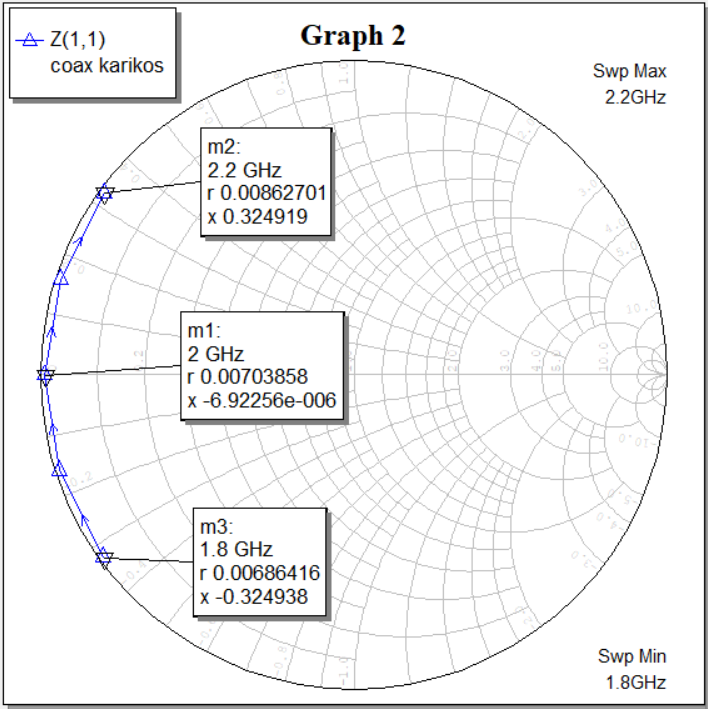
Рисунок 9 — Диаграмма зависимости нормированного входного сопротивления от частоты (R=0)
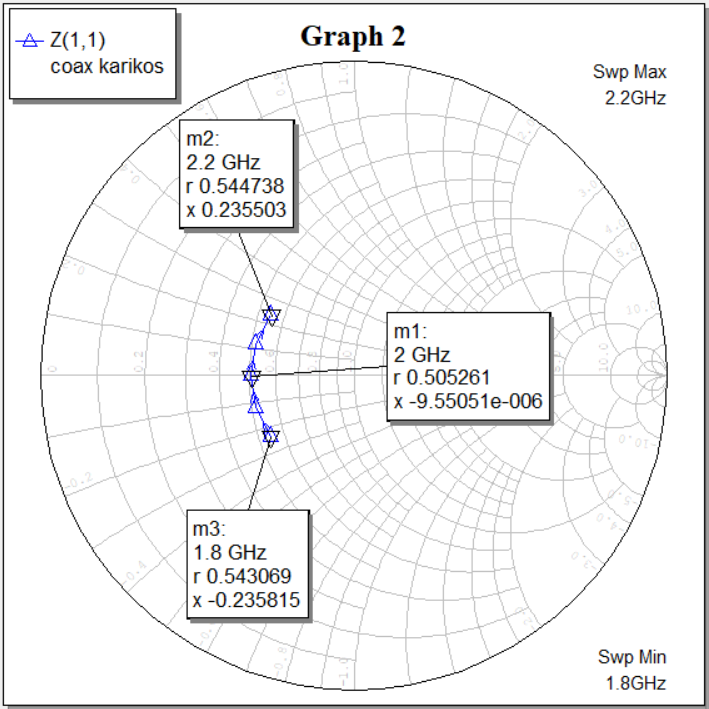
Рисунок 10 — Диаграмма зависимости нормированного входного сопротивления от частоты (R=25 Ом)
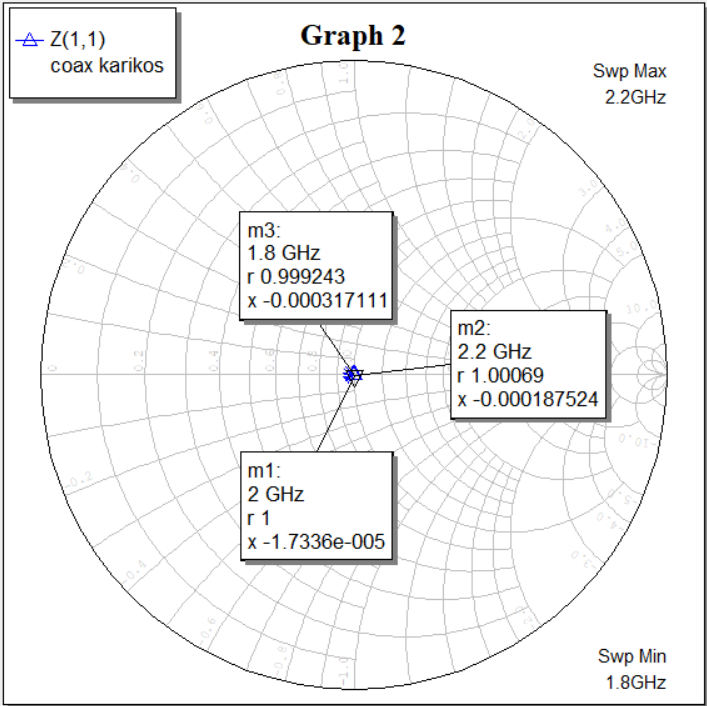
Рисунок 11 — Диаграмма зависимости нормированного входного сопротивления от частоты (R=50 Ом)
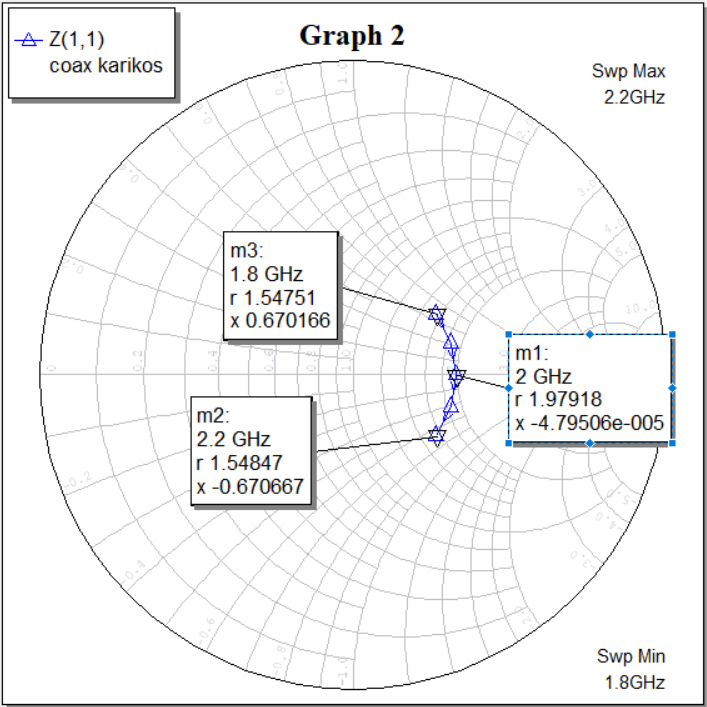
Рисунок 12 — Диаграмма зависимости нормированного входного сопротивления от частоты (R=100 Ом)
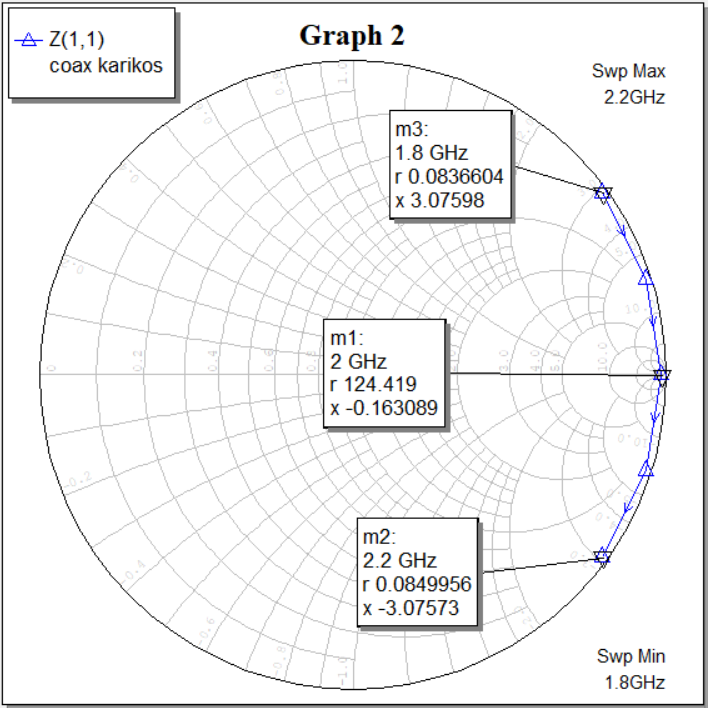
Рисунок 13 — Диаграмма зависимости нормированного входного сопротивления от частоты (R=50 кОм)
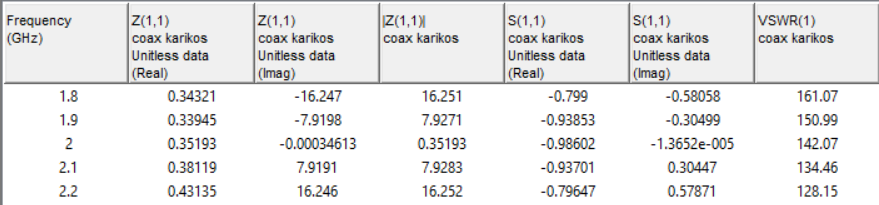
Рисунок 14 — Зависимость входного сопротивления от частоты (R=0 Ом)
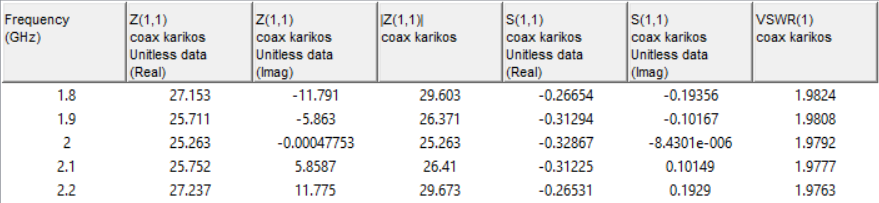
Рисунок 15 — Зависимость входного сопротивления от частоты (R=25 Ом)
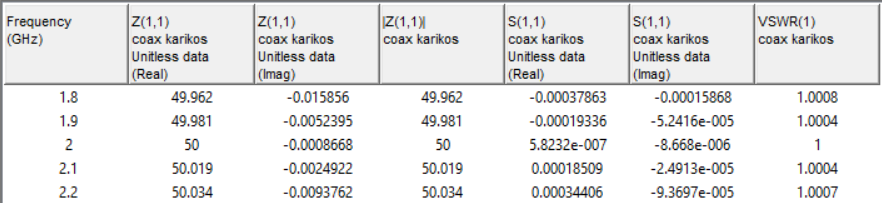
Рисунок 16 — Зависимость входного сопротивления от частоты (R=50 Ом)
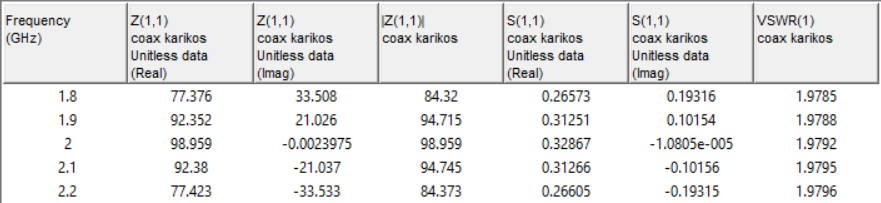
Рисунок 17 — Зависимость входного сопротивления от частоты (R=100 Ом)
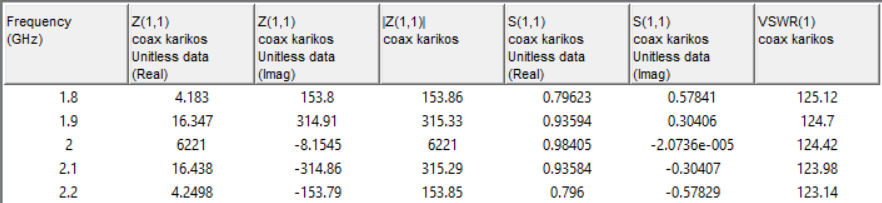
Рисунок 18 — Зависимость входного сопротивления от частоты (R=50 кОм)
2.4 Исследование зависимости нормированного входного сопротивления от электрической длины коаксиальной линии
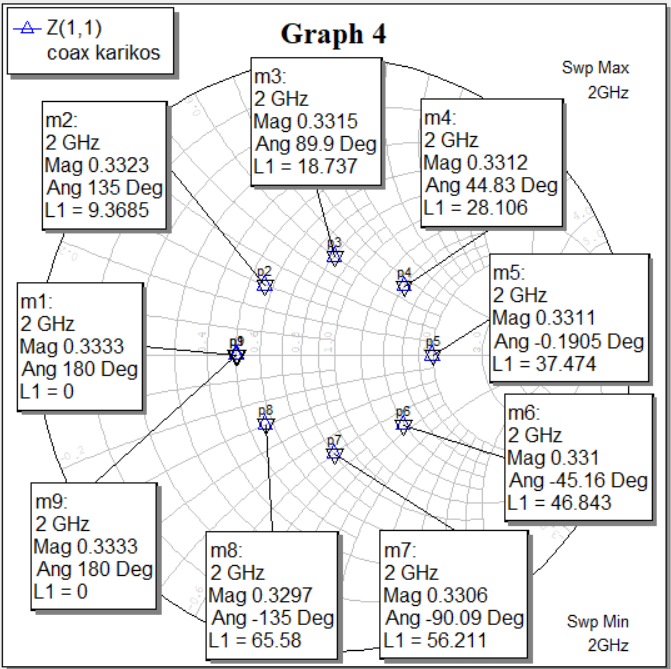
Рисунок 19 — Диаграмма зависимости нормированного входного сопротивления от электрической длины коаксиальной линии от 0 до π с шагом π/8
Вывод: в ходе лабораторной работы были исследованы параметры коаксиальной линии с различными нагрузками. Убедились, что при согласованной нагрузке (Zн = 50 Ом) КСВ ≈ 1, а коэффициент отражения ρн близок к нулю. При рассогласованных нагрузках наблюдались изменения вещественной и мнимой частей входного сопротивления, а также рост КСВ.