4. Рассчитать и построить зависимость электропроводности от толщины металлической плёнки при заданной температуре.

Электропроводность тонкой плёнки как функция толщины определяется следующим интегральным выражением:

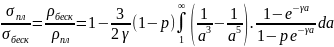
На практике для расчёта электропроводности как функции толщины используют приближенные выражения:

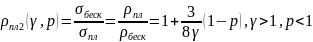
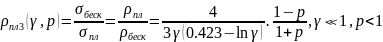
Отметим, что последнее из приведённых соотношение справедливо лишь для малых значений p и γ < 0,5. Толщина плёнки определяется как

При зеркальном отражении электронов от поверхности (p =1) угол падения электронов на поверхность равен углу отражения от поверхности, и проекции импульса электрона в направлении электрического поля, приложенного к образцу, сохраняются, а, следовательно, электропроводность образца не меняется. Т.е. имеем:

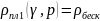
Рассчитаем зависимость электропроводности плёнки от толщины 𝜌_пл(𝑑) для двух значений параметра зеркальности p₁ = 0 и p₂ = 0.4 в заданном диапазоне температур.

Рис. 4.1. Зависимость электропроводности плёнки от толщины при

p₁=0 и 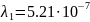(Т =300К)

Рис. 4.2. Зависимость электропроводности плёнки от толщины при

p₁=0 и 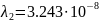(Т =800К)

Рис. 4.3. График суммарной электропроводимости при p₁=0; (Т =300К) и (Т =800К).

Рис. 4.4. Зависимость электропроводности плёнки от толщины при

p₂=0.4 и (Т =300К)

Рис. 4.5. Зависимость электропроводности плёнки от толщины при

p₂=0.4 и (Т =800К)

Рис. 4.6. График суммарной электропроводимости при p₂=0.4; (Т =300К) и (Т =800К).

Вывод: Изменение значений параметра зеркальности p сильно отражается на зависимости электропроводности от толщины. С увеличением p график суммарной электропроводности изменяется. Его начальное значение уменьшается, спад становится наиболее плавным. На графиках 4.3 и 4.6 видно, что при значениях p₂ = 0,4 наблюдается скачок, а при значениях p₁ = 0 ступенчатый спад

5. Определить эффективную массу носителей заряда, их концентрацию и степень электронно-дырчатого газа в собственном полупроводнике в данном диапазоне температур. Рассчитать и построить зависимости концентрации, подвижности и электропроводности от температуры для заданного примесного полупроводника.

5.1) Исследование температурная зависимость энергии Ферми в собственном полупроводнике.

Параметры полупроводника, в данном случае InAs.

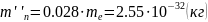
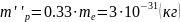
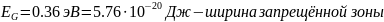
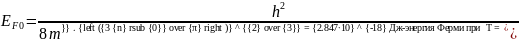
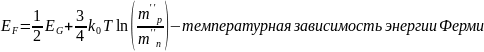
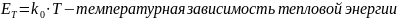
Рис. 5.1. График зависимости энергии Ферми от температуры в собственном полупроводнике.

С ростом температуры энергия Ферми 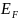немного увеличивается. График зависимости энергии Ферми от температуры показывает, что значение остаётся близким к середине запрещённой зоны, что характерно для собственного полупроводника. Энергия Ферми на всём протяжении больше kT. При низких температурах (T ≈ 0) энергия Ферми значительно больше тепловой энергии (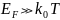 ), поэтому электронный газ можно считать вырожденным. 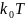С повышением температуры тепловая энергия увеличивается и становится сравнимой с , что приводит к переходу в невырожденное состояние. Таким образом, в обычных температурных условиях (комнатная температура и выше) собственный полупроводник InAs — это невырожденный полупроводник.

5.2) Исследование зависимости концентрации носителей заряда от температуры для собственного полупроводника.

Концентрации электронов n(T) и дырок p(T) при температуре T в собственном невырожденном полупроводнике определяются выражениями:

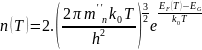
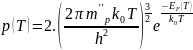
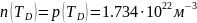
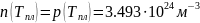
Рис. 5.2.1. Зависимость концентрации носителей заряда от температуры в степени -1

Как видно из результатов, расчётные концентрации электронов численно совпадают с расчётными концентрациями дырок при соответственных значениях температур.

5.3) Исследование зависимости концентрации носителей заряда от температуры для примесного (донорного) полупроводника.

Концентрация собственных электронов описывается формулой:

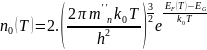
Концентрация электронов донорной примеси описывается формулой:

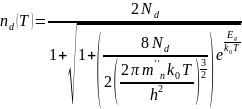
Выберем донорную примесь Se. Расчётное значение энергии активации примесных атомов в InAs равно

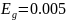
Справедливы следующие аппроксимационные формулы:

Полная концентрация электронов рассчитывается по формуле:

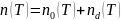
Рис. 5.2.1. Зависимость концентрации носителей заряда от температуры в степени -1 в примесном полупроводнике

Как видно из графика, диапазон температур с постоянной концентрацией отсутствует.

5.4) Исследование зависимости электропроводности от температуры для примесного (донорного) полупроводника.

Электропроводность полупроводников с концентрацией электронов n(T) и дырок p(T) и подвижностью электронов и дырок соответственно μ_n(T)и μ_p(T) определяется как:

Зависимости μ_n(T) и μ_p(T) имеют вид:

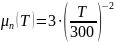
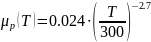
Поскольку в нашей задаче рассматривается полупроводник n-типа, подвижность за счёт электронов не учитывается:

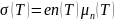
Зависимость электропроводности от температуры в примесном полупроводнике:

Рис. 5.4.1. Зависимость электропроводности от температуры в примесном полупроводнике

Рис. 5.4.2. Зависимость подвижности носителей заряда в примесном полупроводнике от температуры

Вывод: В примесных полупроводниках свободные носители заряда формируются в результате ионизации как примесных, так и собственных атомов. Однако для возбуждения собственного электрона — то есть перевода его из валентной зоны в зону проводимости — требуется энергия, равная ширине запрещённой зоны. В случае же примесных атомов, например доноров, для перехода электрона с примесного уровня в зону проводимости необходима значительно меньшая энергия. Поэтому вклад этих двух процессов в общую концентрацию носителей заряда зависит от температуры и различается при разных условиях.

Экспериментальные зависимости концентрации электронов от температуры можно условно разделить на три характерные области. При низких температурах средняя энергия тепловых колебаний кристаллической решётки недостаточна для полной ионизации доноров, и они остаются частично неионизованными. В результате концентрация свободных электронов остаётся низкой, но с ростом температуры она экспоненциально увеличивается за счёт ионизации примесей. В этом температурном диапазоне основным источником носителей заряда являются переходы электронов с примесных уровней в зону проводимости.