МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра МИТ

ИНДИВИДУАЛЬНЫЕ ДОМАШНИЕ ЗАДАНИЯ

по дисциплине ОЭиРМ

Вариант 4

Выполнил отчет студент гр. фыв		фыв
Преподаватель доцент кафедры МИТ		фыв

Санкт-Петербург

фыв

Исходные данные:

Таблица 1

№ Вариант	Элемент	Структура	Атомная масса	Параметр решетки, Å	Плотность, г/см3	Удельное сопротивле­ние, мкОм·см	Температура, К			Работа выхода Авы, эВ
							Дебая (TD)	Ферми (TF·10-4)	Плавления (Tпл)
6	Fe	ОЦК	55.84	2.87	7.87	9.8	470	13.0	1808	4.31

Таблица 2

№ ВАР.	Тип примеси	Полупроводник	Ширина запрещенной зоны		Эффективная масса		Подвижность при 300К		Работа выхода, эВ
				EG (300 К), эВ	m"n / me	m"p / me	μn, см2·В‑1·с‑1	μp, см2·В‑1·с‑1
5	n	InAs		0.36	0.028	0.33	30000	240	4.90

Таблица 3

№ вар.	6
концентрация примесей, м-3	1025

Задания

1. Определить класс симметрии заданных материалов, построить прямую и обратную элементарные ячейки заданных материалов. Определить размеры Зоны Бриллюэна в направлениях X, L, К.

2. Определить концентрацию электронов для заданного металла из условия касания зоны Бриллюэна и сферы Ферми и сделать суждение о применимости теории свободных электронов.

3. Рассчитать и построить зависимости средней длины свободного пробега, времени релаксации и электропроводности от температуры для металла в диапазоне температур (0,1-10) ТD. Оценить степень дефектности металла по заданной величине удельного сопротивления.

4. Рассчитать и построить зависимость электропроводности от толщины металлической пленки при заданной температуре. Определить минимально возможную толщину металлизации.

5. Определить эффективную массу носителей заряда, их концентрацию и степень вырождения электронно-дырочного газа в заданном примесном полупроводнике в данном диапазоне температур. Рассчитать и построить зависимости концентрации, подвижности и электропроводности от температуры для заданного примесного полупроводника.

6. Построить энергетическую диаграмму заданной пары металл-полупроводник в выбранном масштабе для случаев: без смещения, при прямом и обратном смещениях.

7. Рассчитать концентрацию носителей заряда в заданном полупроводнике для создания омического контакта к металлу.

8. Взять полупроводник, задайте для p-n перехода концентрации донорных N_d и акцепторных N_а примесей, равными 10²⁶, 10²⁰, 10¹⁶ атомов/м³. Сравните полученные ВАХ. Сделайте выводы из полученных результатов. Получив ВАХ и оценив полученные p-n переходы, постарайтесь подумать, что к этим областям необходимо присоединить контакты, чтобы в конкретном изделии использовать переход. В каких областях следует вспомнить о легировании полупроводника, чтобы не образовался встречно включенный диод Шоттки.

9. Выводы

1. Определить класс симметрии заданных материалов, построить прямую и обратную элементарные ячейки заданных материалов. Определить размеры Зоны Бриллюэна в направлениях X, l, к.

Металл: Fe - Железо

Структура: ОЦК (объемноцентрированный куб)

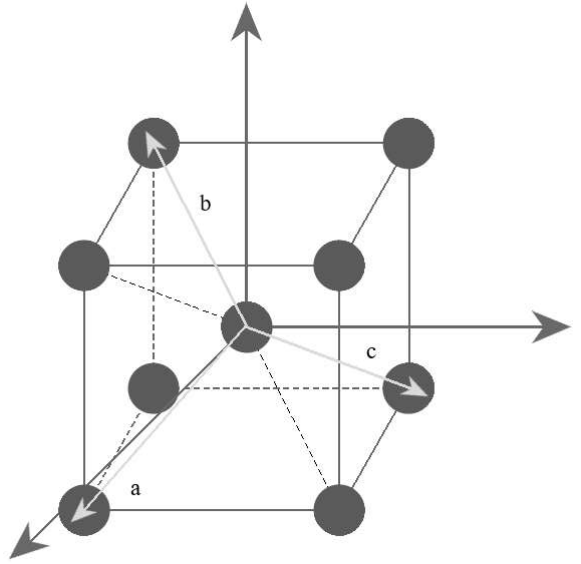
Параметр решётки: а = 2.87 * 10^-10 м

Категория: Высшая

Сингония: Кубическая

Класс симметрии: Аксиально-центральный (m3m)

Формула симметрии: 3L₄4L₃6L₂9PC

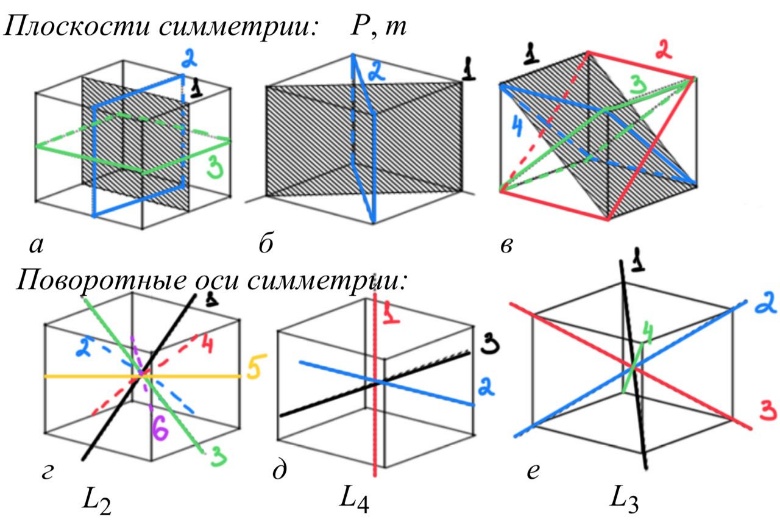
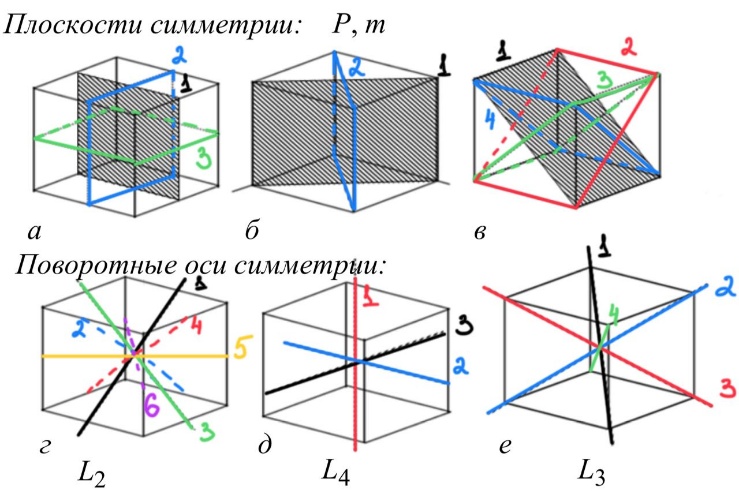
z

Базисные вектора для прямого пространства:

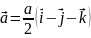
y

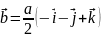
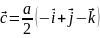
x

Найдём объём ячейки:

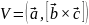
Рис. 1.1. Модель ОЦК

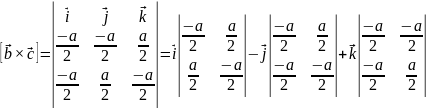
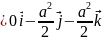
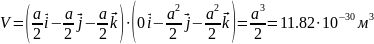
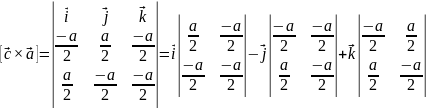
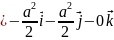
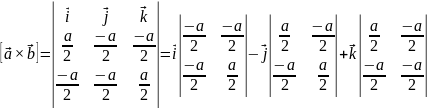
Базисные вектора для обратного пространства:

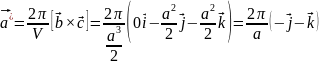
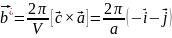
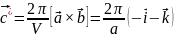
-z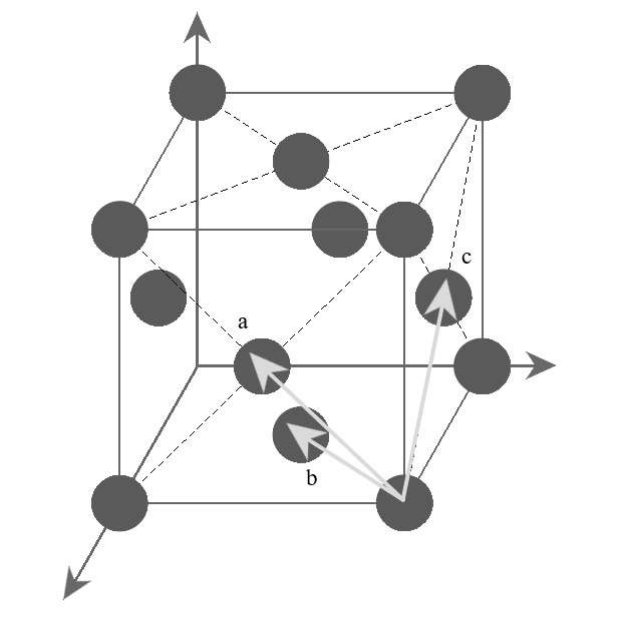

Подставляя параметр решётки получим:

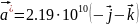
y

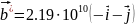
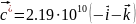
Рис. 1.2. Модель ГЦК

x

Расчёт зоны Бриллюэна для направлений X, L, K

Н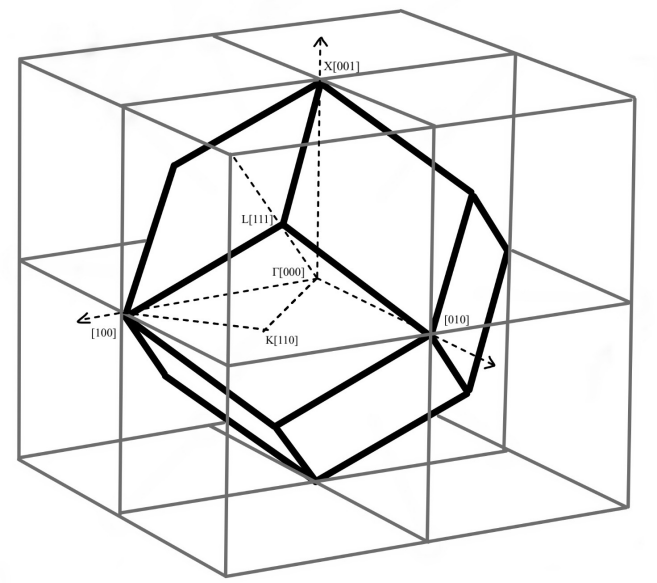 аправление X [001]:

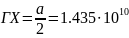м^-1

Направление K [110]:

Г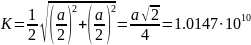 м^-1

Направление L [111]:

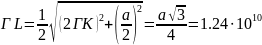м^-1

Рис. 1.3. Ячейка Вигнера-Зейтца

в обр. пространстве

Полупроводник InAs - Арсенид индия

Структура: ГЦК

Параметр решётки: а = 6.06 * 10^-10 м

Категория: Высшая

Сингония: Кубическая

Класс симметрии: Аксиально-центральный (m3m)

Формула симметрии: 3L₄4L₃6L₂9PC

z

Базисные вектора для прямого пространства:

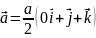
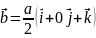
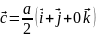
y

Рис. 1.4. Модель ГЦК

x

Найдём объём ячейки:

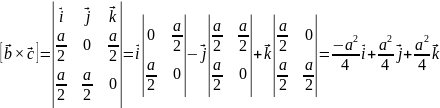
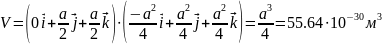
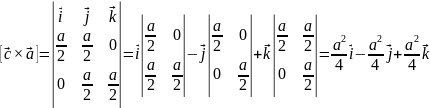
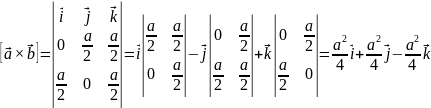
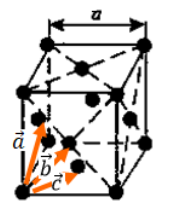
Б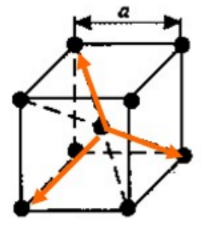 азисные вектора обратной решётки:

y

x

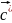
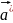
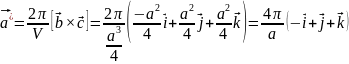
z

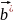
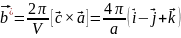
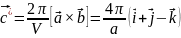
Рис. 1.5. Модель ОЦК

Подставляя параметр решётки получим:

, ,
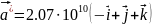
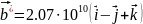