Практика ИДЗ / фомнэ2

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И.Ульянова (Ленина)

Кафедра Микрорадиоэлектроники и технологии радиоаппаратуры (МИТ)

ДЗ № 2

По дисциплине «ФОМНЭ»

Вариант № 4

Выполнил студент гр. фыв		фыв
Преподаватель Доцент кафедры МИТ		фыв

Санкт-Петербург

фыв

Задание.

1. Рассчитать длину волны де Бройля для тела с массой m1, атома М и элементарной частицы А, движущихся с одинаковой скоростью V = 10⁶м/с. Сравните длинны волн между собой и с известными диапазонами длин волн. Сделайте выводы.

2. Определить ошибку в определении физической величины, налагаемой соотношением неопределенности Гейзенберга, зная ∆х – неопределенность в положении частицы равную радиусу атома М. Предположите, что знаете массу с абсолютной точностью и оцените неопределенность скорости тела с массой m1, атома М и элементарной частицы А. Сделайте вывод.

Исходные данные:

№	Фамилия Имя Отчество	m1 (г)	M	A
4	фыв	1	Al	Нейтрон

Задание №1

Формула, использованная для расчёта:

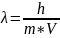, где h = 6,626⋅10⁻³⁴ Дж·с,

Рассчитаем длину волны де Бройля для тела с массой m₁ = 1 г = 0,001 кг:

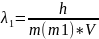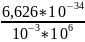= = 6,63 *10^-37 м

Рассчитаем длину волны для атома алюминия с молярной массой M(Al) = 0,027 кг/моль:

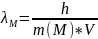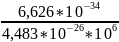= = 1,477 *10^-14 м

Рассчитаем длину волны для нейтрона с массой 1,675⋅10⁻²⁷ кг:

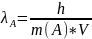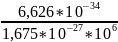= = 3,952 *10^-13 м

Вывод: Тело с меньшей массой (нейтрон) обладает более длинной длиной волны де Бройля по сравнению с атомом алюминия и телом массой 1 г. Это означает, что частицы с меньшей массой проявляют более ярко выраженные волновые свойства при движении с одинаковой скоростью.

Рассчитанные длины волн де Бройля находятся в диапазоне от 6,63 * 10^-37 м до 3,952 *10^-13 м. Сравнивая их с известными диапазонами длин волн, можно увидеть, что длины волн де Бройля для рассмотренных частиц значительно меньше, чем длины волн электромагнитного излучения. Это подтверждает, что волновые свойства частиц проявляются на очень малых масштабах.

Задание №2

Формулы, использованные для расчёта:

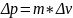— определение импульса частицы

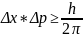— принцип неопределённости Гейзенберга

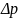— неопределённость в определении проекции импульса частицы,

Примем Δx за размер атома алюминия:

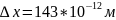
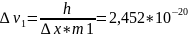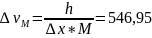м/с

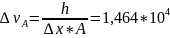м/с

м/с

Вывод: Используя принцип неопределенности Гейзенберга и принимая размер атома алюминия за Δx, мы можем оценить неопределенность в определении скорости частиц (тело массой m1, атом алюминия и нейтрон) при известной неопределенности в положении частицы. Для тела массой m1 = 1 г неопределенность в скорости составляет 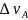≈ 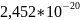м/с. Это очень малая величина, что указывает на высокую точность определения скорости тела при известной неопределенности в положении.

Для атома алюминия неопределенность в скорости составляет ≈ 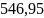м/с. Это значительно больше, чем для тела массой m1, что связано с большей массой атома и, следовательно, с меньшей чувствительностью его скорости к неопределенности в положении.

Для нейтрона неопределенность в скорости составляет ≈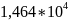 м/с. Это еще больше, чем для атома алюминия, что также связано с его большей массой.

Таким образом, принцип неопределенности Гейзенберга показывает, что чем больше масса частицы, тем больше неопределенность в ее скорости при заданной неопределенности в положении.