Лабораторочки / тоэ7

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ТОЭ

отчет

по лабораторной работе №7

по дисциплине «ТОЭ»

Тема: Исследование резонансных явлений в простых электрических цепях.

Студенты гр. фыв		фыв
		фыв
Преподаватель		фыв

Санкт-Петербург

фыв

Цель работы:

Исследование резонанса и АЧХ последовательного и параллельного колебательных контуров.

Краткие теоретические сведения:

Резонанс – это состояние RLC-цепи в установившемся синусоидальном режиме, при котором напряжение и ток на входе цепи совпадают по фазе.

Существует два вида резонанса в электрических цепях:

- Резонанс напряжений – наблюдается в последовательном контуре.

- Резонанс токов – проявляется в параллельном контуре.

Для обеих цепей резонансная частота определяется формулой:

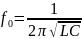
При резонансе:

• В последовательном контуре комплексное сопротивление становится вещественным, а модуль проводимости достигает максимального значения:

​

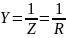
Максимальный ток в цепи:

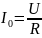
Добротность последовательного контура определяется как:

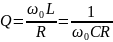
• В параллельном контуре максимальным становится модуль его комплексного сопротивления:

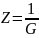
Максимальное напряжение:

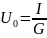
Добротность параллельного контура выражается формулой:

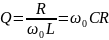
АЧХ последовательного и параллельного контуров определяется зависимостью модуля проводимости и сопротивления от частоты соответственно:

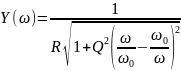и

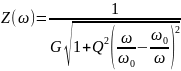
Обработка результатов измерений.

1) Исследование резонанса напряжений и АЧХ контура с малыми потерями.

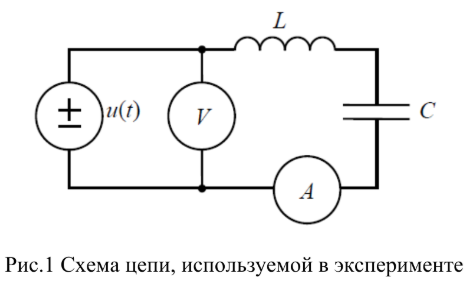
Рисунок 1. Схема цепи, используемой в эксперименте

Данные, измеренные и вычисленные при резонансной частоте:

Измерить				Вычислить
U, В	I0, мА	f0, кГц	UC0, В		R, Ом	Q	ρ, кОм	L, Гн	C, мкФ
2	10,89	4,8	35,9		183,6	17,95	3,3	0,109	0,011

Таблица 1. Контур с малыми потерями.

ω = 30,2 кГц

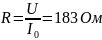
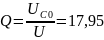
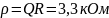
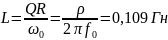
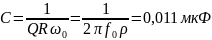
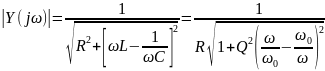
Расчет зависимости тока от частоты:

f, кГц	2,4	2,9	3,4	3,9	4,4	4,8	4,9	5,4
i, мА	0,65	1,08	1,26	1,68	3,92	10,89	8,38	3,17
|Y|*10-6, См	202,1	288,2	429,9	718,9	1658,2	5445,0	4376,3	1250,4

f, кГц	6,4	6,9	7,4	7,9	8,4	8,9	9,6
I, мА	0,71	0,66	0,58	0,49	0,41	0,37	0,33
|Y|*10-6, См	517,7	407,8	339,0	291,8	257,1	230,5	202,1

Таблица 2. Расчет резонансной кривой.

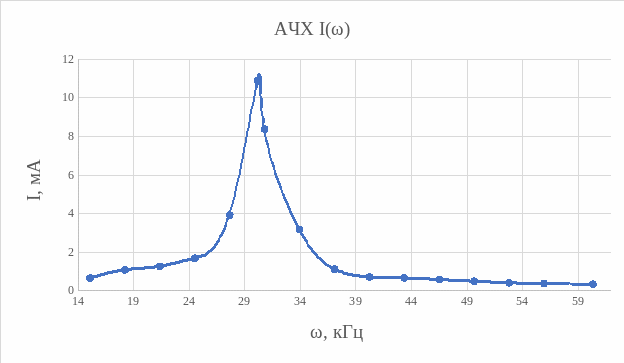
Вопрос №1: как, используя эквивалентные схемы цепи для ω=0, ω→∞ и

ω=ω0, определить значения АЧХ на этих частотах и проконтролировать

результаты эксперимента?

Эквивалентные схемы цепи позволяют определить граничные значения амплитудно-частотной характеристики (АЧХ):

При ω=0 (низкая частота):

Конденсатор ведет себя как разрыв цепи (X_C​→∞),

Индуктивность – как короткое замыкание (X_L​→0),

Ток определяется только активным сопротивлением R.

При ω→∞ (высокая частота):

Индуктивность ведет себя как разрыв (X_L​→∞),

Конденсатор – как короткое замыкание (X_C→0),

Ток также ограничивается активным сопротивлением R.

При ω=ω₀​ (резонансная частота):

Реактивные сопротивления катушки и конденсатора компенсируют друг друга (X_L=X_C​), цепь становится чисто активной с минимальным полным сопротивлением, а ток достигает максимального значения, проводимость – своего пика.

Проверка экспериментальных данных включает: сравнение рассчитанных и измеренных значений резонансной частоты, анализ АЧХ, определение частоты, при которой проводимость максимальна, вычисление добротности и проверка соответствия расчетам.

2) Исследование резонанса напряжений и АЧХ контура с большими потерями.

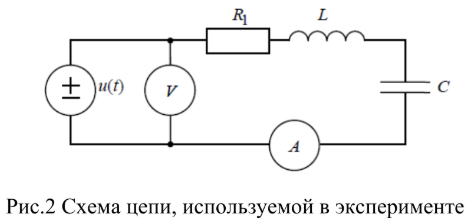
Рисунок 2. Схема цепи, используемой в эксперименте.

Данные, измеренные и вычисленные при резонансной частоте:

Измерить				Вычислить
U, В	I0, мА	f0, кГц	UC0, В	R, Ом	Q	ρ, кОм	L, Гн	C, мкФ
2	3,01	4	10,11	664,45	5,06	3,4	0,133	0,012

Таблица 3. Контур с большими потерями.

ω = 25,1 кГц

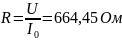
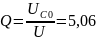
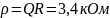
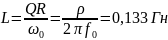
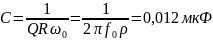
f, кГц	1,5	1,8	2,1	2,4	2,7	3	3,3	3,7
i, мА	0,3	0,36	0,48	0,64	0,8	1,07	1,48	2,02
|Y|*10-6, См	129,4	167,0	213,6	274,4	358,5	483,3	684,8	1181,5

f, кГц	4	4,3	4,7	5	5,3	5,7	6
i, мА	3,07	2,4	1,79	1,64	1,37	1,14	0,9
|Y|*10-6, См	1505,0	1214,5	784,4	605,7	493,2	397,1	347,6

Таблица 4. Расчет резонансной кривой.

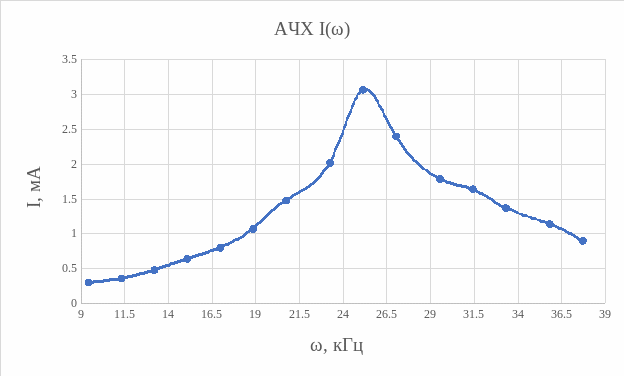
Вопрос №2: в чём сходство и в чем различие данных, измеренных и

рассчитанных в пунктах 1) и 2)?

Сходства:

В обоих случаях наблюдается резонансная частота, при которой максимален ток.

Добротность цепи определяется соотношением Q = f₀/Δf

АЧХ имеет характерный пик на резонансной частоте.

Различия:

Контур с большими потерями (R больше) имеет меньшую добротность (Q), то есть резонансный пик более сглажен.

В контуре с малыми потерями резонансный ток выше, так как суммарное сопротивление цепи при резонансе меньше.

Резонансная частота в контуре с большими потерями может быть немного ниже из-за влияния активного сопротивления.

3) Исследование влияния емкости на характеристики контура.

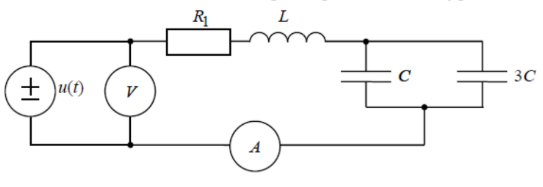
Рисунок 3. Схема цепи, используемой в эксперименте.

Данные, измеренные и вычисленные при резонансной частоте:

Измерить				Вычислить
U, В	I0, мА	f0, кГц	UC0, В	R, Ом	Q	ρ, кОм	L, Гн	C, мкФ
2	3,21	2,9	5,06	623,05	2,53	1,58	0,087	0,035

Таблица 5. Контур с большими потерями.

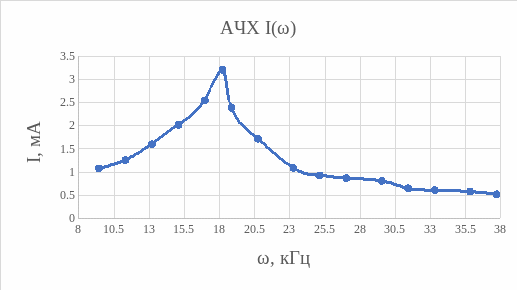
ω = 18,2 кГц

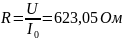
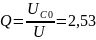
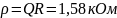
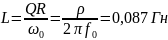
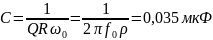
Рассчитаем зависимость тока от частоты:

f, кГц	1,5	1,8	2,1	2,4	2,7	3	3,3	3,7
i, мА	1,68	2,05	2,6	3,2	1,74	1,39	1,19	1,09
|Y|*10-6, См	431,5	594,9	827,6	1155,9	1509,2	1581,9	1342,2	1005,1

f, кГц	4	4,3	4,7	5	5,3	5,7	6
i, мА	0,93	0,87	0,81	0,65	0,61	0,58	0,52
|Y|*10-6, См	829,9	705,0	588,1	524,1	473,4	420,3	388,2

Таблица 6. Расчет резонансной кривой.

Вопрос №3: В чем сходство и в чем различие данных в пунктах 2) и 3)?

Сходства:

В обоих случаях наблюдается резонанс, определяемый частотой ω₀​.

С ростом активного сопротивления добротность контура уменьшается.

Форма АЧХ схожа, но отличается по амплитуде и ширине пика.

Различия:

В третьем пункте влияние емкости на характеристики контура более выражено.

Изменение емкости сказывается на резонансной частоте f₀.

При увеличении емкости резонансная частота уменьшается, а полоса пропускания становится шире.

Вывод:

В ходе лабораторной работы исследованы резонансные явления в последовательных и параллельных RLC-контурах. Установлено, что:

В резонансном режиме реактивные сопротивления компенсируются, и цепь ведет себя как чисто активная.

Добротность контура влияет на ширину и амплитуду резонансной кривой: чем выше Q, тем более выражен пик резонансной частоты.

Увеличение активного сопротивления снижает добротность и сглаживает резонанс.

Изменение емкости влияет на резонансную частоту, уменьшая её при увеличении C.

Полученные экспериментальные данные соответствуют теоретическим расчетам, что подтверждает достоверность проведенных измерений.