Лабораторочки / тоэ3

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ТОЭ

отчет

по лабораторной работе №3

по дисциплине «ТОЭ»

Тема: Исследование свободных процессов в электрических цепях.

Студенты гр. фыв		фыв
		фыв
Преподаватель		фыв

Санкт-Петербург

фыв

Цель: изучение связи между видом свободного процесса в электрической цепи и расположением ее собственных частот (корней характеристического уравнения) на комплексной плоскости; экспериментальное определение собственных частот и добротности RLC-контура по осциллограммам.

Схема установки:

Р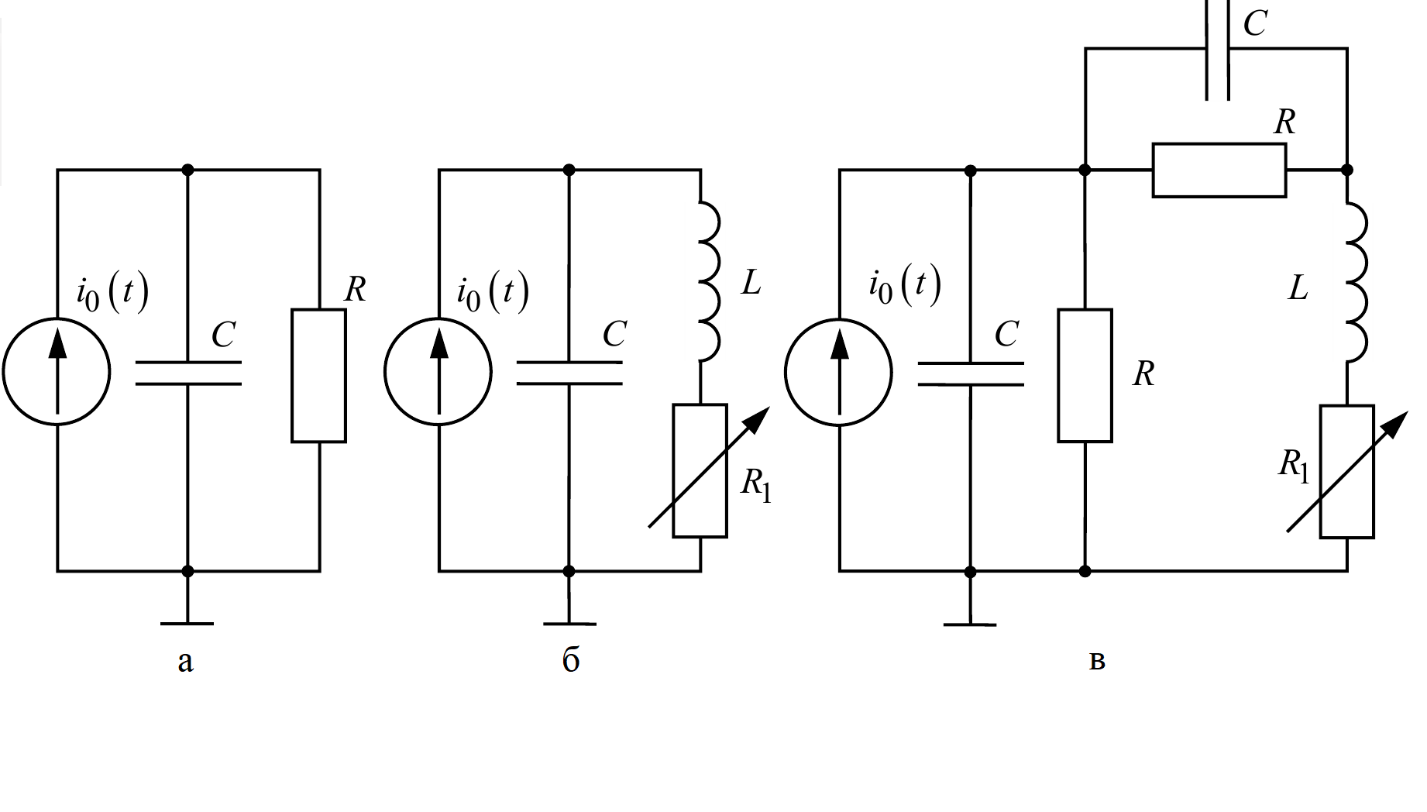 ис. 1. Схема установки исследования свободных процессов в электрических цепях: а – первого порядка, б – второго порядка, в – третьего порядка.

Основные расчетные формулы.

1. Формула для расчета собственной частоты p₁ (Гц) у цепи первого порядка: p₁ = 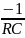, где R – сопротивление резистора (Ом), C – емкость конденсатора (Ф).

Собственная частота p₁ по осциллограмме:

p₁ = -α = 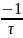, где α – постоянная затухания, для осциллограммы: α =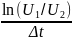 , 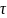– постоянная времени. И U₁ – напряжение по осциллограмме в момент времени t₁, U₂ - напряжение по осциллограмме в момент времени t₂. Δt = t₂-t₁

2. Формула для расчета собственной частоты p_1,2 (Гц) у цепи второго порядка при колебательном процессе: p_1,2 = -α ± 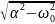*j, где

α = R₁/(2L), 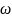₀ = 1/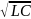 . L – индуктивность катушки (Гн).

Частота ω = 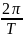, где T – период.

Собственная частота p_1,2 по осциллограмме должная удовлетворять условию Δt=T!

3. Формула для расчета собственной частоты p_1,2 = p₁ = p₂ по осциллограмме для критического режима:

p_1,2=-α = 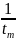, где

t_m – момент наступления максимума.

4. Формула для расчета экспериментальной добротности цепи второго порядка Q:

Q =

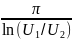
5. Формула для расчета теоретической добротности Q цепи второго порядка: Q=

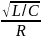
Обработка результатов эксперимента.

3.2.1. Исследование свободных процессов в цепи первого порядка.

Теоретическая собственная частота цепи:

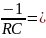
p₁ = 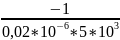= -10 000 с^-1 = -10⁴ с^-1

Практическая собственная частота цепи (по осциллограмме):

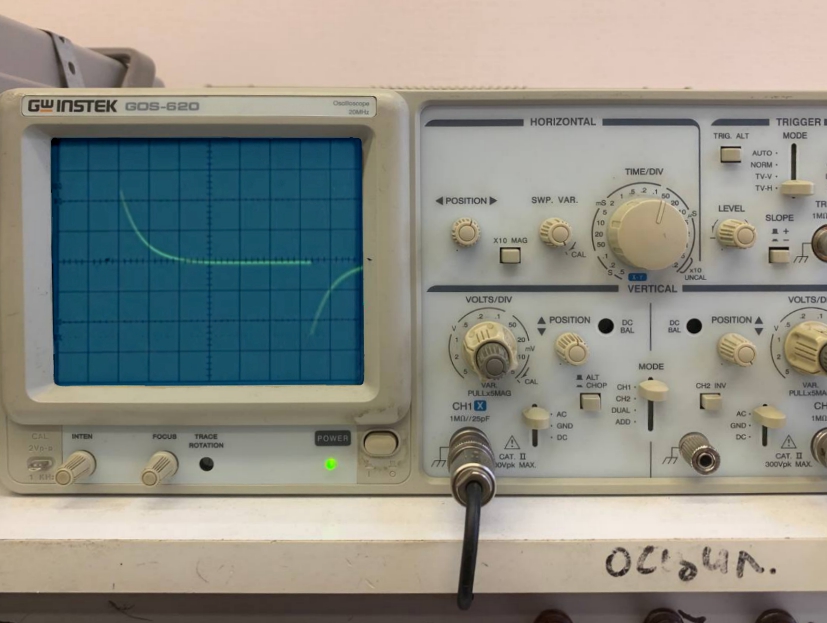
Рисунок 1 - Осциллограмма свободного процесса в цепи 1-го порядка (апериодический режим)

p₁ = -α = ; α = = 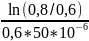= 9589,40242 с^-1

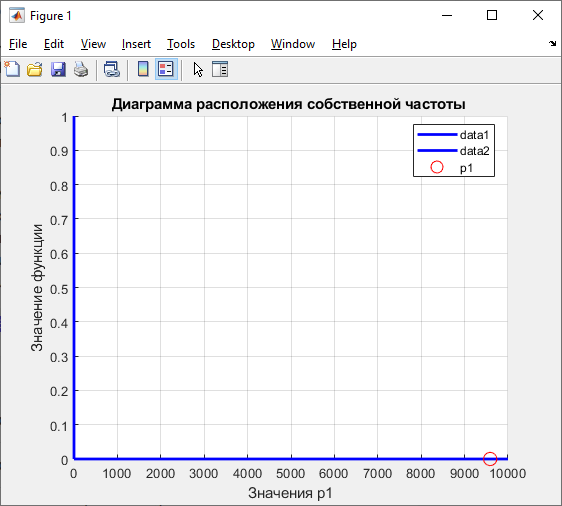
В данной цепи установившийся апериодический режим, потому на экране наблюдается экспоненциальный режим, откуда можно сделать вывод, что аналитическое выражение будет следующим: 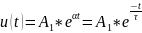. Найденная практическая собственная частота немного ниже теоретической предположительно из-за расчетов, но даже при этом, погрешность составила < 5%.

3.2.2. Исследование свободных процессов в цепи второго порядка.

1) Теоретическая собственная частота цепи при R₁ = 0,5 кОм (колебательный режим):

p_1,2 = -α ± * j

α = R₁ / (2L) = 0,5*10³ / (2*25*10^-3) = 10⁴

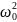= 1 / LC = 1 / ( = 2 * 10⁹

p_1,2 = -10⁴ ± 4,36*10⁴ * j с^-1

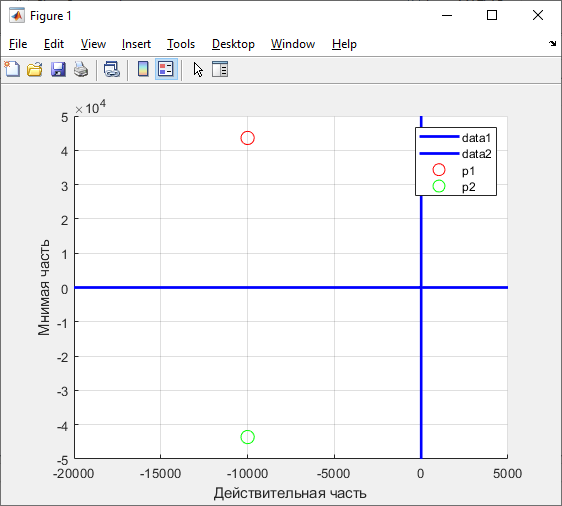
Практическая собственная частота цепи:

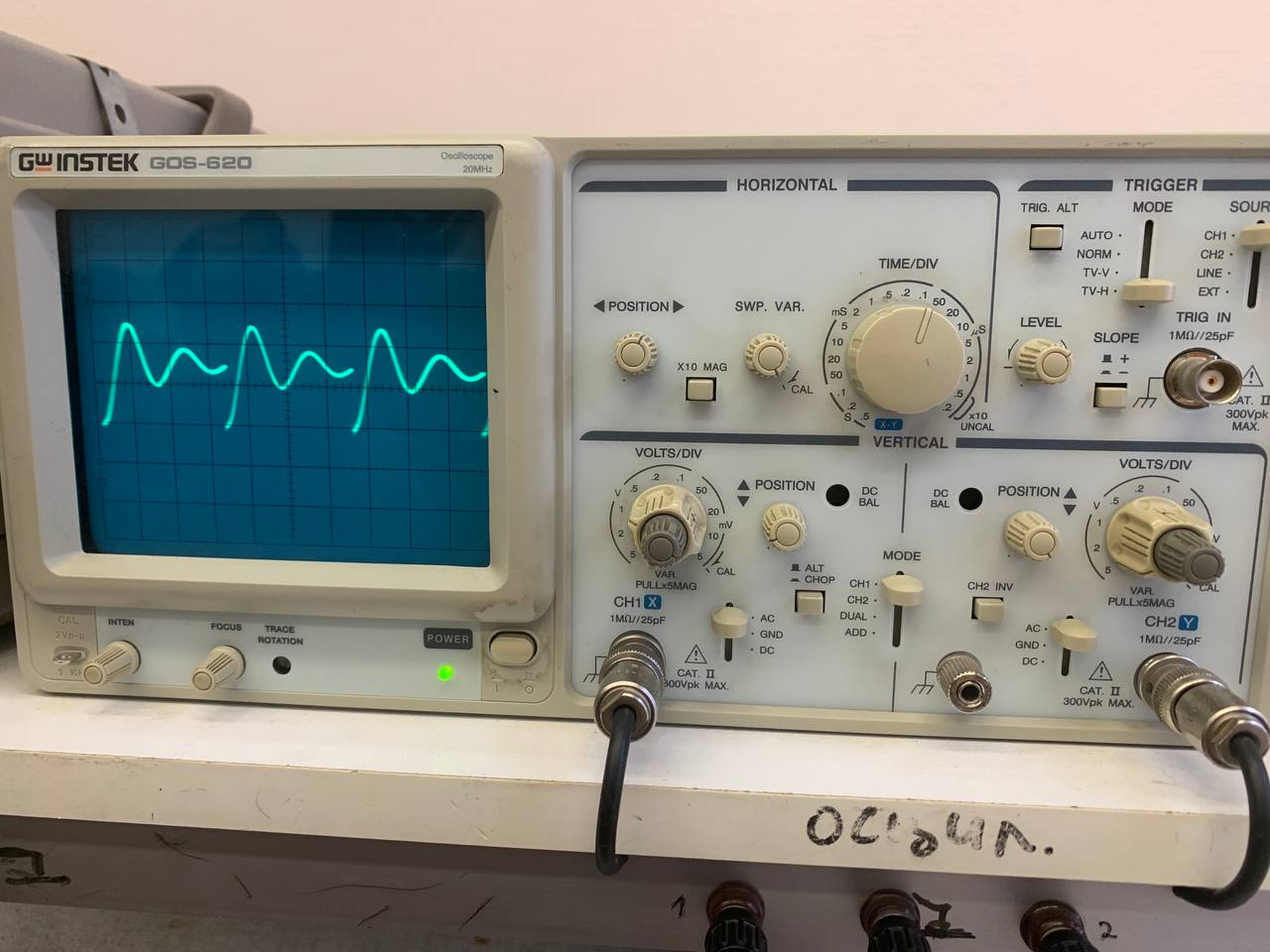
Рисунок 2 - Осциллограмма колебательного режима в цепи 2-го порядка

p_1,2 = - α ± jω = ; α = = 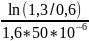≈ 9664,8736 с^-1.

ω = ≈ 78539,8163 с^-1.

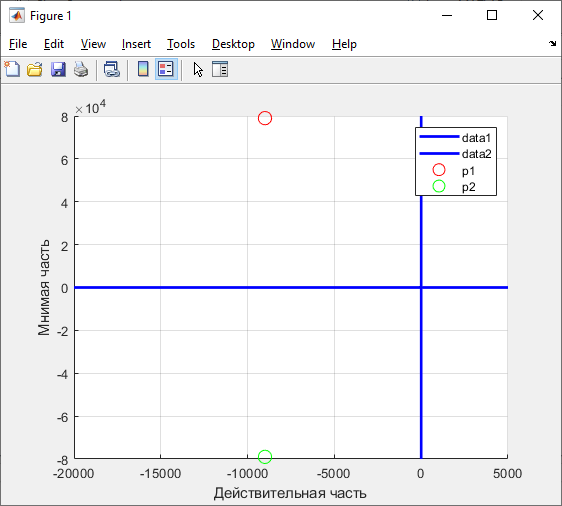
p_1,2 ≈ -0,9*10⁴ ± 7,9*10⁴ * j с^-1.

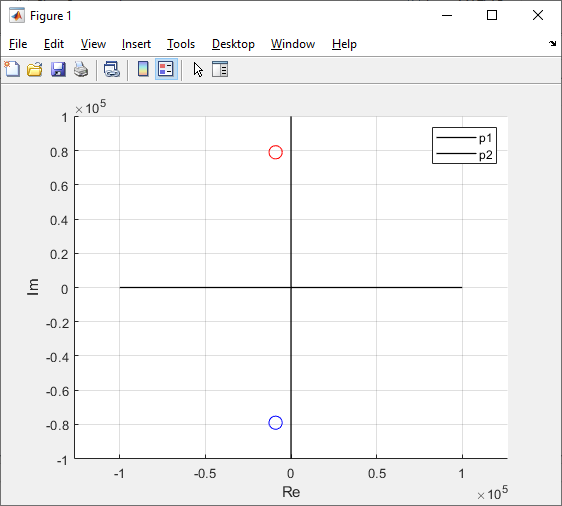
Q = =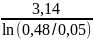 ≈ 4,06

2) Теоретическая собственная частота цепи при R₁ = 0,5 кОм (апериодический режим):

p_1,2 = -α ± ;

α = R₁/(2L) = 3*10³/(2*25*10^-3) = 6 * 10⁴.

= 1/LC=1/( =2 * 10⁹

p_1,2 ≈ -(6*10⁴)±3,64*10⁴ с^-1.

Собственная частота цепи по осциллограмме:

Рисунок 3 - Осциллограмма апериодического режима цепи 2-го порядка

p_1,2= -α ± jω = ; α = = 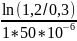≈ -36651,6293 с^-1

ω = ≈ 125663,7061 с^-1

p_1,2 ≈ -3,66*10⁴ ± 12,56*10⁴ с^-1

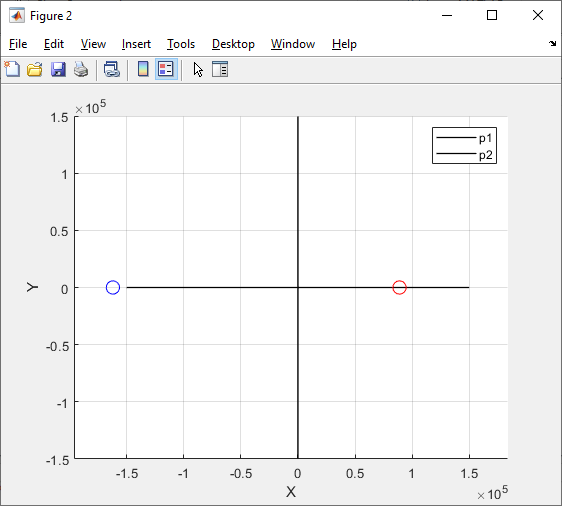
3) Теоретическая собственная частота цепи при R₁ = R_кр = 1,3 кОм (установленный по осциллограмме критический режим):

p_1,2 = -α ± ;

α = R₁/(2L) = 1,3*10³ / (2*25*10^-3) = 26000.

= 1/LC=1 / ( = 2 * 10⁹

p_1,2 ≈ -(2,6*10⁴) ± 3,64*10⁴ с^-1

4) Теоретическая собственная частота цепи при R₁ = 0:

p_1,2 = ± jω₀;

ω₀ = 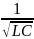= 44721,3595

p_1,2 ≈ ± 4,47*10⁴*j с^-1.

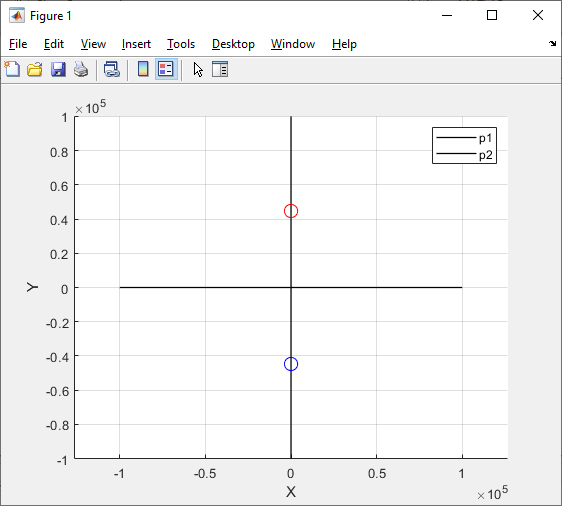
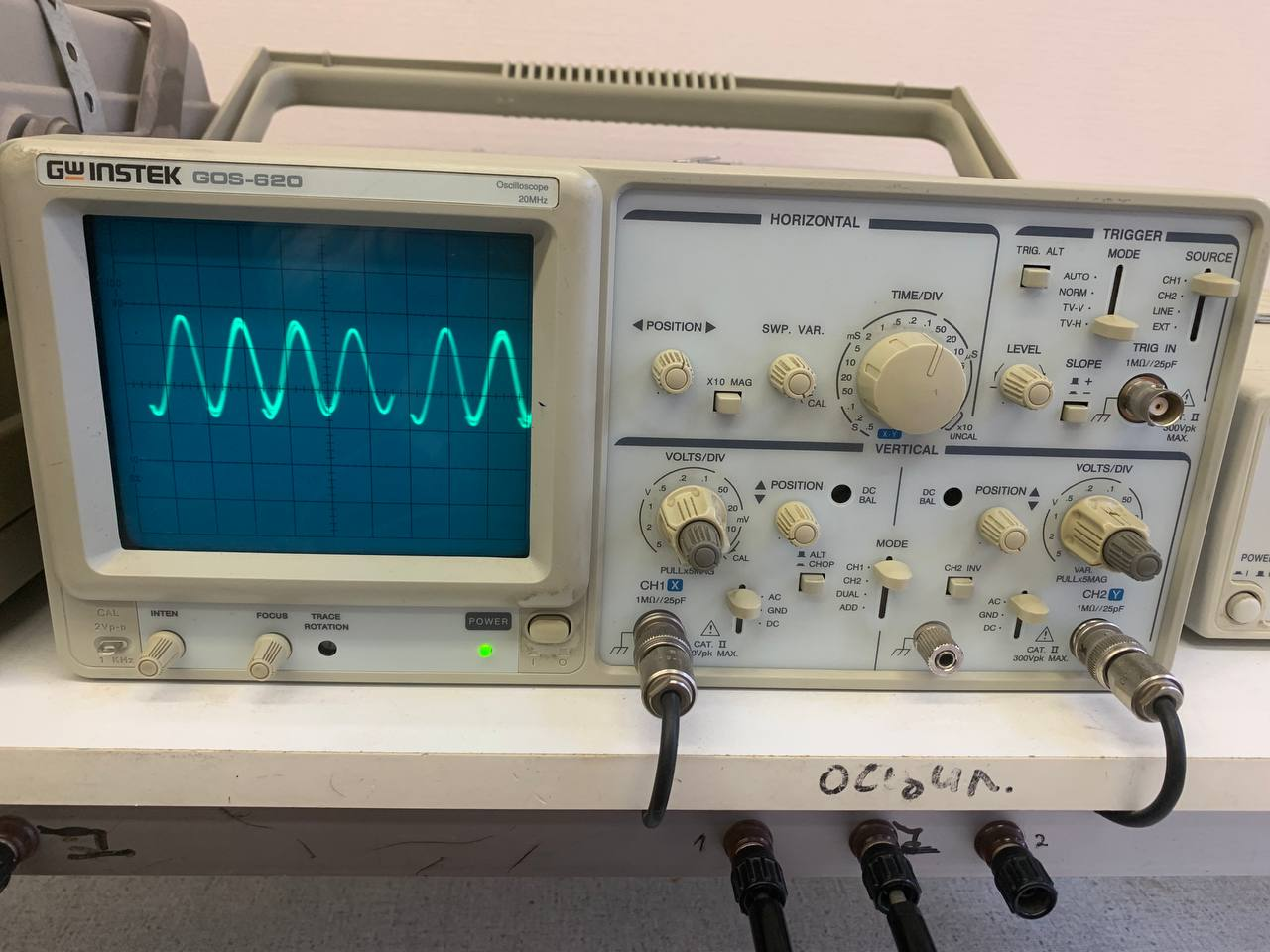
Рисунок 4 - Осциллограмма цепи 2-го порядка при R₁=0

Q → ∞, т.к. режим колебательный незатухающий, в цепи нет потребителей и присутствует резонанс.c

Во всех четырех случаях графики процессов описываются следующим аналитическим выражением:

где  - постоянные интегрирования,  - порядок цепи;

Соответствие, найденных собственные частоты теоретическому расчету, зависит от режима. Теоретические и экспериментальные значения были близки, но имелись расхождения, обусловленные погрешностями измерений и неидеальностью компонентов.

При R1 = 3 кОм и значениях L и C, указанных в отчете, цепь находится в апериодическом режиме.

Теоретические значения собственных частот: p1,2 ≈ -(610^4)±3,6410^4 с-1. Небольшие расхождения добротности обусловлены погрешностями измерений.

3.2.3. Исследование свободных процессов в цепи третьего порядка

Расчет теоретического значения собственной частоты контура для цепи третьего порядка:

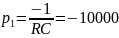
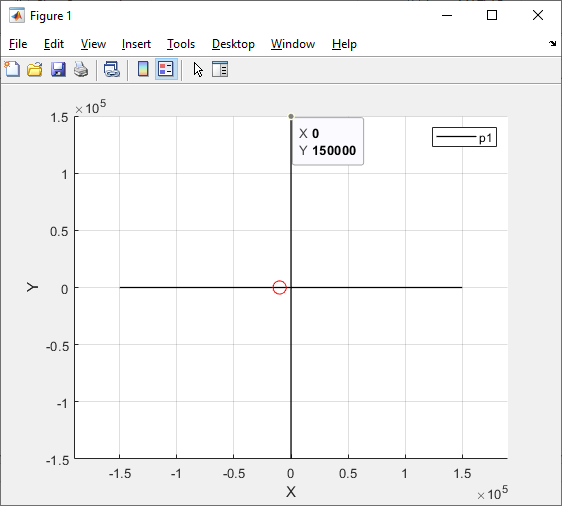
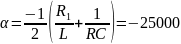
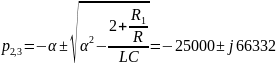
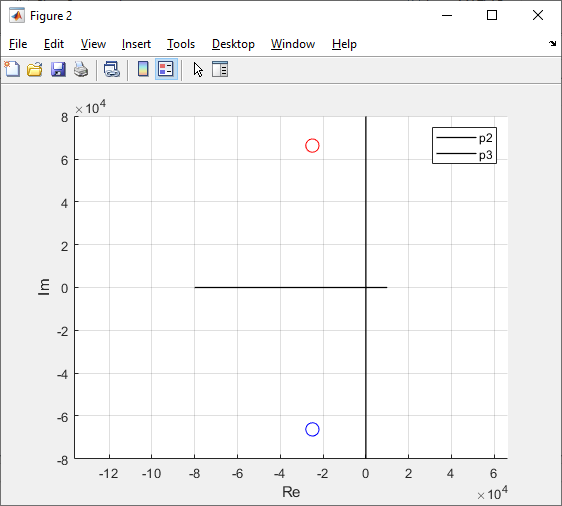
Осциллографируемый процесс описывается выражением:

U_C(t) = Ae^-10000t

Вывод:

В данной лабораторной работе исследовались свободные процессы в электрических цепях первого, второго и третьего порядков с целью изучения взаимосвязи между видом переходного процесса и расположением собственных частот на комплексной плоскости, а также экспериментального определения собственных частот и добротности RLC-контура. В цепи первого порядка (RC-цепь) наблюдался апериодический режим разряда конденсатора, описываемый экспоненциальным законом, где собственная частота определяла скорость затухания. Практическое значение собственной частоты, полученное по осциллограмме, показало незначительное отклонение от теоретического расчета, что подтверждает корректность модели и точность измерений. В цепи второго порядка (RLC-цепь) были исследованы колебательный, апериодический и критический режимы. Колебательный режим характеризовался наличием затухающих колебаний, где практические значения собственной частоты и добротности были определены по осциллограмме, а теоретические значения рассчитаны по формулам. Различие между теоретическими и экспериментальными значениями объясняется погрешностями измерений и неидеальностью компонентов схемы. Апериодический режим продемонстрировал монотонное затухание без колебаний, в то время как критический режим, достигнутый подбором сопротивления, представлял собой наиболее быстрое затухание без колебаний. При отсутствии сопротивления (R=0) наблюдался незатухающий колебательный процесс, что соответствовало резонансу в цепи. В цепи третьего порядка были рассчитаны теоретические значения собственных частот. В целом, работа подтвердила зависимость вида переходного процесса от параметров цепи и, соответственно, расположения корней характеристического уравнения, продемонстрировав связь между математической моделью и реальным поведением электрической цепи.