Спектральный анализ входного одиночного сигнала

Определим спектральные характеристики одиночного входного сигнала:

Представим входной сигнал в экспоненциальной форме:

Тогда комплексный спектр сигнала будет выглядеть так:

Тогда амплитудный спектр сигнала будет иметь следующий вид:

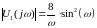
Рисунок 6. Амплитудный спектр входного одиночного сигнала

Фазовый спектр соответственно:

Рисунок 7. Фазовый спектр входного одиночного сигнала

Определим полосу пропускания цепи.

Рисунок 8. Определение полосы пропускания цепи

Максимальная амплитуда составляет ≈ 5,83.

Уровень –3 дБ (0,707 от максимума):

0,707 ∙ 5,83 ≈ 4,13.

Граничные частоты: левая граница ω₁ = 0,56, правая граница ω₂ = 1,84. Полоса пропускания вычисляется как разность граничных частот: Δω = ω₂​ − ω₁ =​ 1,84 − 0,56 = 1,28.

Коэффициент искажения .

Оценим время запаздывания сигналов, спектр которых попадает в полосу пропускания.

Рисунок 9. Определение времени запаздывания сигналов

Формула времени запаздывания:

Построим график амплитудно-фазовой характеристики.

Рисунок 10. График амплитудно-фазовой характеристики

Амплитудный и фазовый спектры выходного сигнала

Найдём амплитудный и фазовый спектры выходного сигнала.

Комплексный спектр сигнала будет выглядеть так: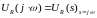

Листинг 1. Вид U_R(jω) в MathCad

Амплитудный спектр сигнала будет иметь следующий вид:

Листинг 2. Вид амплитудного спектра сигнала U_R(jω) в MathCad

Рисунок 11. Амплитудный спектр выходного одиночного сигнала

Фазовый спектр соответственно:

Листинг 3. Вид фазового спектра сигнала U_R(jω) в MathCad

Рисунок 12. Фазовый спектр выходного одиночного сигнала

Амплитудный и фазовый спектры периодического входного сигнала

Определим амплитудный и фазовый спектры периодического входного сигнала. По условию, период сигнала равен удвоенному времени импульса Т = 8.

Рисунок 13. Графики исходного входного периодического сигнала

и сигнала, представленного рядом Фурье

Периодический сигнал можно представить в виде экспоненциальной формы ряда Фурье: где ​  — циклическая частота сигнала, C_k​ — комплексные коэффициенты Фурье, вычисляемые по формуле , а также постоянную составляющую С₀ = 0.

Сигнала m1(t), который принимает значения 2, 0 и -2 на разных интервалах, интеграл разбивается на соответствующие участки:

Для АЧХ: (для четных: 0 или 1; для нечетных: );

Для ФЧХ: .

Листинг 4. Первые 9 гармоник ряда Фурье входного периодического сигнала

Рисунок 14. Амплитудный дискретный спектр входного периодического сигнала (10 гармоник)

Рисунок 15. Фазовый дискретный спектр входного периодического сигнала

Рисунок 16. Входной сигнал, полученный из разложения ряда Фурье

Приближенный расчет реакции цепи по спектру при периодическом воздействии

Для приблизительного расчета отклика системы на периодический сигнал используется спектральный подход. Сначала исходный периодический сигнал раскладывается на гармонические составляющие с определенными амплитудами и частотами. Затем каждая такая составляющая корректируется с учетом влияния цепи - ее амплитуда и фаза изменяются согласно характеристикам системы. После этого все обработанные гармонические компоненты складываются вместе, что дает итоговый выходной сигнал.

Частота первой гармоники: ;

Коэффициенты Фурье для меандра: ;

Передаточная функция: ;

Выходной спектр получается умножением каждой гармоники входного сигнала на передаточную функцию: ;

Формулы для амплитуды и фазы выходного сигнала:

;

Выходной сигнал можно приближенно записать как сумму гармоник:

или как в вещественной форме: .

Листинг 5. Первые 9 гармоник ряда Фурье выходного периодического сигнала

Рисунок 17. Амплитудный дискретный спектр выходного периодического сигнала

Рисунок 18. Фазовый спектр выходного периодического сигнала.

Рисунок 19. Выходной сигнал, полученный из разложения ряда Фурье