matlab laboratornye / матлаботчет2

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра РС

отчет

по лабораторной работе №2

по дисциплине «MATLAB»

Тема: Основы работы в среде MATLAB.

Работа в режиме прямых вычислений

с векторами и матрицами.

Студент гр. фыв		фыв
Преподаватель		фыв

Санкт-Петербург

фыв

Цель работы.

Знакомство со способами задания переменных-векторов и переменных-матриц; освоение принципов выполнения основных матричных операций; знакомство с поэлементными действиями.

Основные теоретические положения.

1. Переменная-вектор: <имя переменной>=[x1 x2 ... xn]

2. Матрица:

   • Строчный формат: <имя>=[x₁₁ x₁₂ ... x_1n; x₂₁ x₂₂ ... x_2n; ...; x_n1 x_n2 ... x_nn]

   • Блочный формат: <имя>=[x₁₁ x₁₂ ... x_1n

x₂₁ x₂₂ ... x_2n

...

x_n1 x_n2 ... x_nn]

3. Элементы матриц/векторов могут быть арифметическими выражениями.

4. Вывод матрицы: <имя>

5. Доступ к элементу: <имя>(i, j)

6. Расширение матрицы по вертикали: <имя>=[<матрица1>; <матрица2>]

7. Расширение матрицы по горизонтали: <имя>=[<матрица1>, <матрица2>]

8. Транспонирование: <имя>'

9. Поэлементные операции:

   • Сложение: <матрица1> + <матрица2>

   • Вычитание: <матрица1> - <матрица2>

10. Поэлементное умножение/деление:

<матрица1>*<матрица2> или <матрица1>/<матрица2>

11. Символ ":" для последовательностей и создания векторов/матриц.

Копии рабочей области MatLab.

1).

Рисунок 1 - Ввод V и M.

Осуществлён ввод переменной-вектора V и матрицы M, а также их вывод на экран.

2).

Рисунок 2 - Ввод L и R

Введены матрица L и вектор R, состоящий из элементов, заданных в виде арифметических вычислений, осуществлён их вывод на экран.

3).

Рисунок 3 - Вывод элемента матрицы М

Определено значение элемента 2 строки 2 столбца в матрице M.

4).

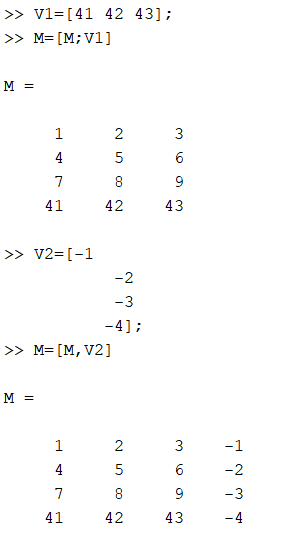
Рисунок 4 - Расширение матрицы

К квадратной матрице размером 3*3 добавлена четвертая строка со значениями 41, 42 и 43 в первом, втором и третьем столбцах соответственно, в результате чего матрица стала размером 4*3. Затем получившейся матрице добавлен четвертый столбец со значениями -1, -2, -3 и -4 в первой, второй, третьей и четвертой строке соответственно, вследствие чего матрица приобрела размер 4*4.

5).

Рисунок 5 - Ошибка при вертикальном расширении матрицы М

Рисунок 6 - Ошибка при горизонтальном расширении матрицы М

Так как размер матрицы M 4*4, то исходя из правил работы с матрицами, нельзя добавить любой столбец (строку), если его (её) количество элементов не совпадает с размерностью рассматриваемой матрицы. В данном случае, чтобы расширить матрицу M, нужно создать переменную-столбец (переменную-строку), содержащий(-ую) 4 элемента.

Рисунок 7 - Правильное вертикальное расширении матрицы М

Теперь матрица М имеет размер 5*4. При добавлении столбца, матрица станет квадратной.

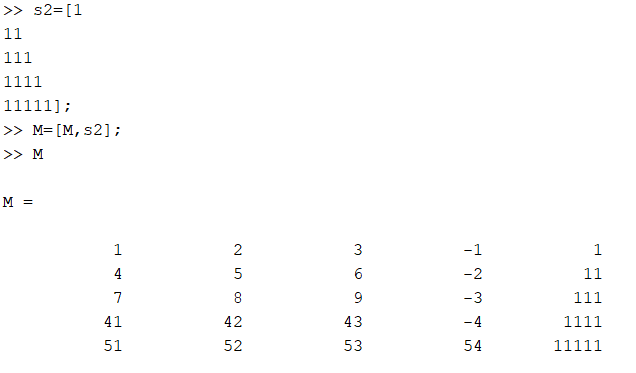
Рисунок 8 - Правильное горизонтальное расширении матрицы М

После добавления столбца матрица М имеет размерность 5*5, после чего мы её можем называть квадратной.

6).

Рисунок 9 - Ввод матриц с комплексными элементами Z и Z1 и вывод их вещественных и мнимых частей

Заданы и выведены на экран матрицы с комплексными элементами Z и Z1 размером 2*2. [real(Z1), real(Z);] объединяет вещественные части элементов матриц Z1 и Z в одну матрицу X, где запятая используется для горизонтального объединения. [imag(Z1), imag(Z);] объединяет мнимые части элементов матриц Z1 и Z в одну матрицу Y, где запятая используется для горизонтального объединения.

7).

Рисунок 10 - Создание матриц, элементы которых равны нулю

Функция zeros используется для создания матрицы или массива, заполненного нулями. В данном случае, zeros(2,3) создает матрицу размером 2*3, состоящую из нулей. Аналогично, zeros(3) создает квадратную матрицу размером 3*3, также заполненную нулями.

Рисунок 11 - Создание матриц, элементы которых равны единице

Функция ones используется для создания матрицы, заполненной единицами. Синтаксис ones(m, n), где m и n - целые числа, указывающие размер матрицы. Следовательно, первоначально ones(2.3) содержит синтаксическую ошибку. Функция возвращает матрицу размером m на n, где каждый элемент равен 1. На изображении первая команда B1=ones(2,3) создает матрицу 2x3, заполненную единицами, которая затем отображается как B1. Вторая команда B2=ones(5) создает матрицу 5x5, заполненную единицами, как указано в отображаемой матрице B2.

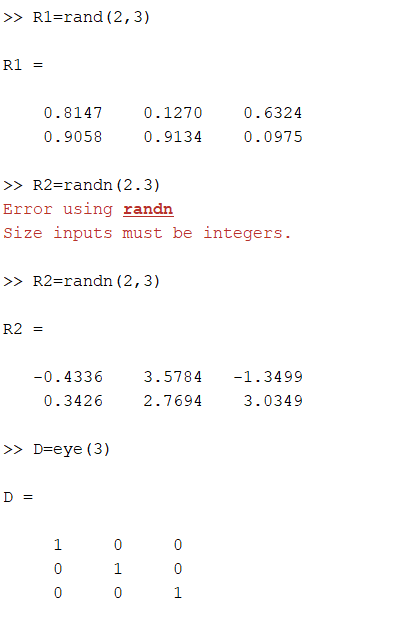
Рисунок 12 - Создание матриц R1 и R2 со случайными значениями элементов и матрицы D с единицами в элементах главной диагонали и нулями в остальных

R1=rand(2,3) создает матрицу размером 2*3 случайных чисел от 0 до 1. R1 - это матрица с шестью случайными десятичными числами. R2=randn(2,3) создает матрицу размером 2*3 случайных чисел из стандартного нормального распределения. Сообщение об ошибке "Error using randn Size inputs must be integers." указывает на то, что входные размеры должны быть целыми числами, и команда не выполняется правильно. D=eye(3) создает квадратную матрицу размером 3*3, элементы которой на главной диагонали равны 1, а остальные - 0.

8).

Рисунок 13 - Использование оператора “:” для создания матрицы-столбца и заполнения элементов матрицы значениями от 10 до 15 построчно

Создана матрица А1 размером 2*3. В1=А1(:) преобразует матрицу А1 в вектор В1, выстраивая все элементы матрицы в одном столбце. A1(:) = 10:15 заполняет все элементы матрицы A1 значениями от 10 до 15. Поскольку A1 имеет 6 элементов, значения от 10 до 15 заполнят матрицу построчно.

Рисунок 14 - Вывод 3-го столбца матрицы L1

Создана матрица L1 размером 3*5. L1(1:3, 3) выбирает все строки и третий столбец из матрицы L1. L1(2:4,2:5) выбирает строки с 2 по 4 и столбцы с 2 по 5 из матрицы L1. Допущена логическая ошибка, ведь функция запрашивает элементы из 4 и 5 строк, которых не существует в матрице L1.

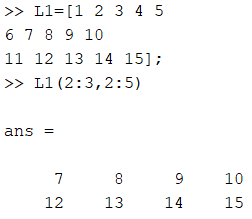
Рисунок 15 - Исправление ошибки при выводе части элементов матрицы L1

Для исправления ошибки (рис.14) для вывода взяв на одну строку меньше можно получить матрицу размером 2*4.

Рисунок 16 - Арифметические действия с элементами матриц

Заданы матрицы А и В с одинаковыми размерами. Элементы матрицы С будут иметь значения, равные сумме соответствующих элементов матриц А и В. Размер матрицы С такой же, как и у матриц А и В. V=V-1 вычитает единицу из каждого элемента матрицы V и присваивает матрицу этой же переменной.

Рисунок 17 - Арифметические действия с элементами матриц

Заданная переменная MU является матрицей, элементы которой численно равны произведениям соответствующих элементов матриц А и В. Заданная переменная DE1 является матрицей, элементы которой равны элементам матрицы А соответственно деленным на элементы матрицы В. Заданная переменная DE2 является матрицей, элементы которой равны элементам матрицы В соответственно деленным на элементы матрицы А.

9).

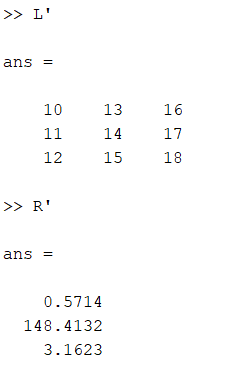
Рисунок 18 - Транспонирование матриц

L' транспонирует матрицу L. R' транспонирует вектор R, превращая его в столбец.

Вывод.

В ходе выполнения лабораторной работы были изучены и практически применены основные операции с векторами и матрицами в среде MATLAB. Были рассмотрены различные способы создания векторов и матриц, включая явное задание элементов, использование функций `zeros`, `ones`, `rand`, `randn` и конструкции `:` для создания последовательностей. Также были освоены операции над векторами и матрицами, такие как сложение, вычитание, умножение, деление, транспонирование и работа с элементами матриц.

Особое внимание уделено было пониманию различий между поэлементными операциями и операциями над матрицами в целом. Было продемонстрировано, как правильно использовать индексацию для доступа к элементам матриц и векторов, а также для изменения их значений.

В процессе работы были выявлены и исправлены ошибки, связанные с неправильным использованием размерностей матриц и векторов при выполнении операций, что позволило лучше понять требования к согласованности размеров при работе с математическими объектами в MATLAB.

Полученные навыки работы с векторами и матрицами в MATLAB являются фундаментальными для дальнейшего изучения и применения этой программной среды в решении различных задач, связанных с обработкой данных, численными методами и инженерными расчетами.