matlab laboratornye / матлаботчет6

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра РС

отчет

по лабораторной работе №6

по дисциплине «MATLAB»

Тема: Операции с многочленами и

возможности обработки данных в MATLAB

Студент гр. фыв		фыв
Преподаватель		фыв

Санкт-Петербург

фыв

Цель работы:

Изучение функций работы с полиномами; знакомство с аппроксимацией и интерполяцией данных; знакомство с функциями расчета выборочных статистик

Краткие теоретические сведения:

I. Пусть задан многочлен P(x)=a₁xⁿ+a₂x^n-1+…+a_n-1x+a_n.

Для нахождения его корней необходимо выполнить следующие действия:

1. Задать вектор-строку коэффициентов многочлена

2. Получить вектор корней многочлена с помощью функции roots.

Формат функции:

<имя вектора корней>=roots(<имя вектора коэффициентов>)

II. Пусть заданы корни многочлена x1, x2, …, xn и необходимо определить его коэффициенты. Тогда нужно выполнить следующие действия:

1. Задать вектор корней

2. Получить вектор коэффициентов многочлена с помощью функции poly. Формат функции:

<имя вектора коэффициентов>=poly(<имя вектора корней>)

III. Для вычисления значения полинома P(x)=a1x n+a2x n-1+…+an1x+an в точке x =s следует:

1. Задать вектор-строку коэффициентов многочлена.

2. Использовать функцию polyval.

Формат функции:

<имя переменной со значениями многочлена> = polyval (<ИмяПеременнойСКоэффициентамиМногочлена>, <значения х>)

IV. Функция conv (a, b) используется для умножения полиномов p(x) и g(x), где a и b – векторы коэффициентов полиномов p(x) и g(x) соответственно.

V. Функция deconv (a, b) используется для деления полиномов p(x) и g(x), где a и b – векторы коэффициентов полиномов p(x) и g(x) соответственно. Результат работы функции – объединенный вектор [q, r], где вектор q – частное, вектор r – остаток от деления.

VI. Функция polyder (p) используется для вычисления производной полинома p(x), где p – вектор коэффициентов полинома p(x). Результат работы функции – вектор коэффициентов производной dp(x)/dx

Копии рабочей области MATLAB:

Найти корни многочлена: P(x) = x⁵+8x⁴+31x³+80x²+94x+20.

» pol=[1 8 31 80 94 20];

» r=roots(pol)

Убедиться, что функция poly восстанавливает коэффициенты многочлена по его корням.

»pol2=poly(r)

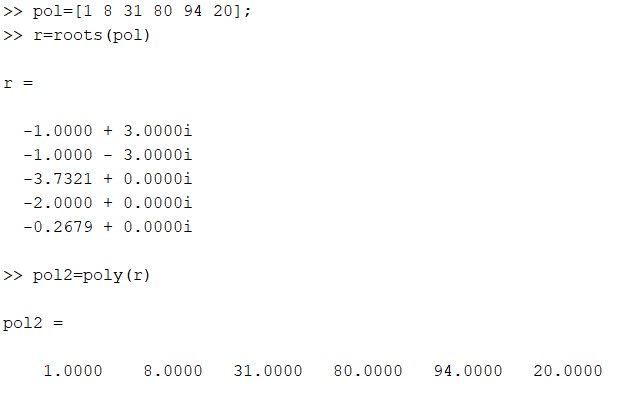
Рисунок 1 - Корни многочлена

Пусть экспериментальная последовательность задана в виде таблицы:

x	2	4	6	8	10
y	1,5	6,3	4,8	8	2,6

Последовательность в виде матрицы, содержащей 2 строки и 5 столбцов (строка №1 - значения х, строка №2 – значения у):

» xydata=[2 4 6 8 10;1.5 6.3 4.8 8 2.6];

Выполнить вызовы следующих функций. Самостоятельно, просматривая результат на экране, определить принцип работы каждой из функций (кроме функции std)

» [n,p]=size(xydata) - позволяет сохранить в памяти машины и использовать потом при дальнейших вычислениях данные о числе строк n и столбцов p этой матрицы

» max(xydata) - выдает значение максимального элемента этого вектора

» min(xydata) - извлекает минимальный элемент вектора

» mean(xydata) - определяют, соответственно, среднее значение элементов вектора

Рисунок 2 - Работа с функциями в матрице

» std(xydata) - % стандартное (квадратичное) отклонение

» sort(xydata) - формирует вектор, элементы которого расположены в порядке возрастания их значений

» sum(xydata) - вычисляет сумму элементов вектора

» prod(xydata) - выдает произведение всех элементов вектора

» diff(xydata) - создает вектор, который имеет размер на единицу меньший размера исходного вектора, элементы которого являются разностью между соседними элементами исходного вектора

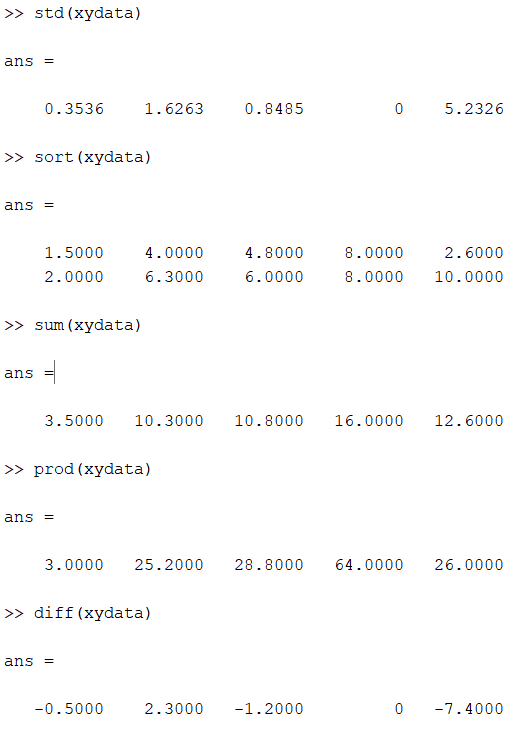
Рисунок 3 - Работа с функциями в матрице

Дана экспериментальная зависимость:

x	2	4	6	8	10	12	14
y	3,76	4,14	5,04	5,56	6,00	6,36	6,64

Задать вектор х

» х=[2 4 6 8 10 12 14];

Задать вектор у

» у=[3.76 4.14 5.04 5.56 6.00 6.36 6.64];

Найти коэффициенты аппроксимирующего многочлена второй степени:

» kAP=polyfit(x,y,2)

Вычислить значения аппроксимирующего многочлена в точках х:

» AP=polyval(kAP,x)

Построить на одном графике исходную зависимость y(x) и вычисленную приближенную AP(x), при этом пометить маркерами точки, соответствующие исходной последовательности (тип узловой точки выбрать самостоятельно).

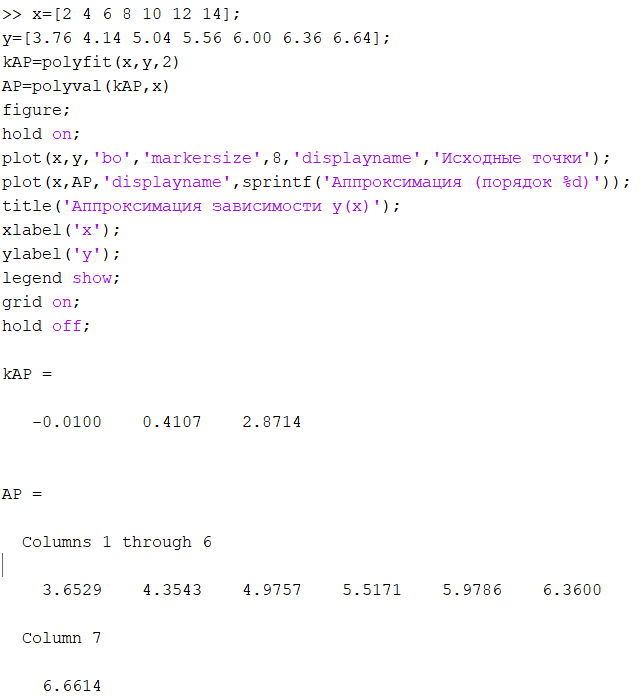
Рисунок 4 – Код для построения аппроксимации многочлена 2-ого порядка

Увеличивая порядок аппроксимирующего полинома от 2 до 6, пронаблюдать приближение результата аппроксимации к исходной зависимости.

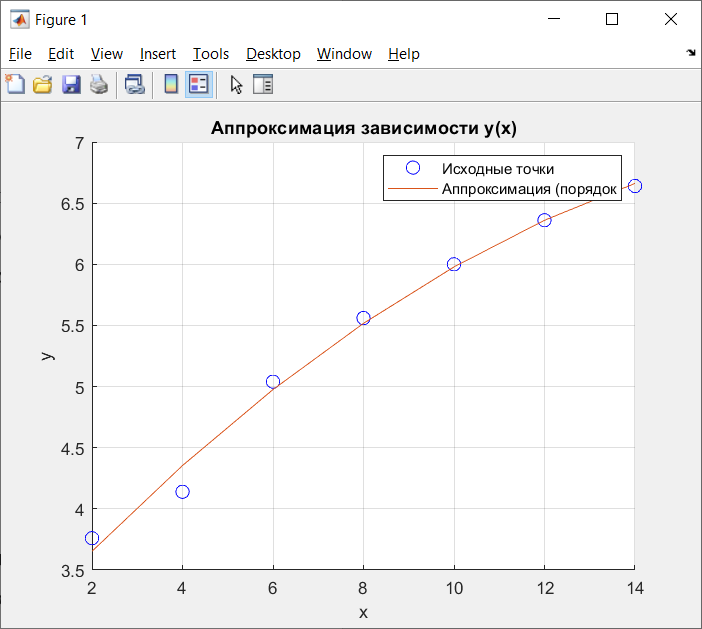
Рисунок 5 - Аппроксимация многочлена 2-го порядка

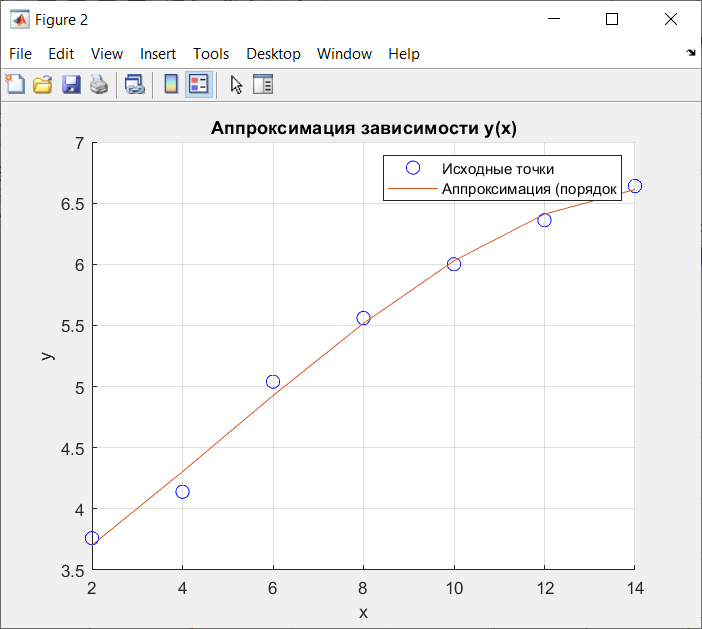
Рисунок 6 - Аппроксимация многочлена 3-го порядка

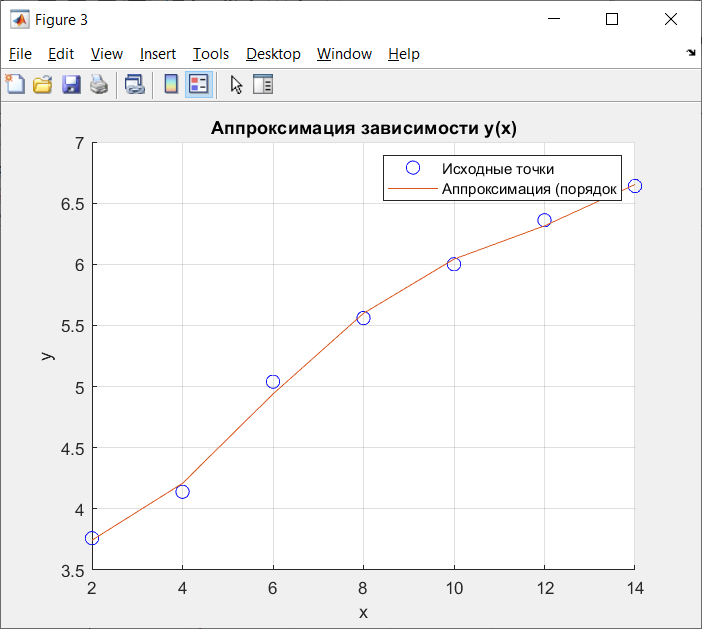
Рисунок 7 - Аппроксимация многочлена 4-го порядка

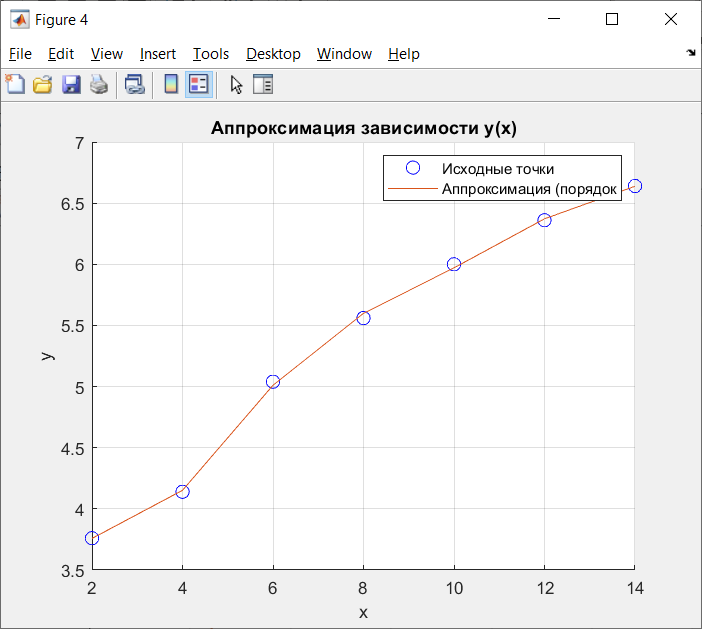
Рисунок 8 - Аппроксимация многочлена 5-го порядка

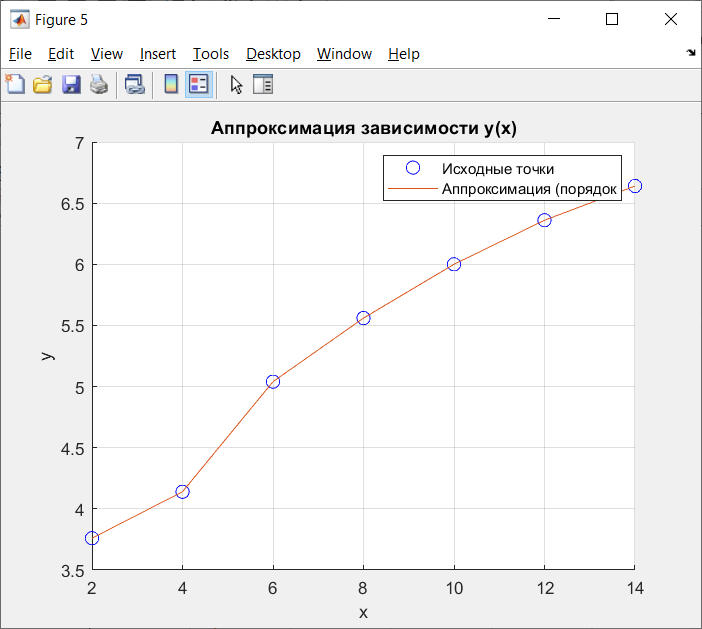
Рисунок 9 - Аппроксимация многочлена 6-го порядка

Пример-задача:

Создать m-файл, позволяющий: задать синусоиду на одном периоде 10-ю точками; исходную 10-титочечную сетку по оси абсцисс определить в переменной х, а исходную для интерполяции последовательность – в переменной у. Задать новую более "мелкую" сетку: за период синусоиды в ней должно уложиться уже 50 точек. Осуществить интерполяцию исходной последовательности, используя все возможные методы. Результаты сохранять в переменных yi<условный номер метода>. Отобразить в первом графическом окне исходную последовательность и результат интерполяции всеми методами. Имя m-файла – interpol.m (сохранить в рабочем каталоге своей группы).

Текст m-файла задачи.

function interpol

x = linspace(0, 2*pi, 10); % 10 точек на интервале [0, 2*pi]

y = sin(x); % Значения синусоиды на исходной сетке

% Задание более мелкой сетки (50 точек на период)

x_fine = linspace(0, 2*pi, 50);

% Интерполяция всеми возможными методами MATLAB

yi1 = interp1(x, y, x_fine, 'linear'); % Линейная интерполяция

yi2 = interp1(x, y, x_fine, 'nearest'); % Ближайший сосед

yi3 = interp1(x, y, x_fine, 'next'); % Следующий сосед

yi4 = interp1(x, y, x_fine, 'previous'); % Предыдущий сосед

yi5 = interp1(x, y, x_fine, 'pchip'); % PCHIP (piecewise cubic Hermite % interpolating polynomial)

yi6 = interp1(x, y, x_fine, 'cubic'); % Кубическая интерполяция

yi7 = interp1(x, y, x_fine, 'spline'); % Сплайн-интерполяция

% Отображение результатов

figure;

plot(x, y, 'o', 'DisplayName', 'Исходный'); hold on;

plot(x_fine, yi1, '-', 'DisplayName', 'Linear');

plot(x_fine, yi2, '--', 'DisplayName', 'Nearest');

plot(x_fine, yi3, ':', 'DisplayName', 'Next');

plot(x_fine, yi4, '-.', 'DisplayName', 'Previous');

plot(x_fine, yi5, '-', 'DisplayName', 'PCHIP');

plot(x_fine, yi6, '--', 'DisplayName', 'Cubic');

plot(x_fine, yi7, ':', 'DisplayName', 'Spline');

% Настройка графика

title('Интерполяция синусоиды');

xlabel('x');

ylabel('y');

legend('show');

grid on;

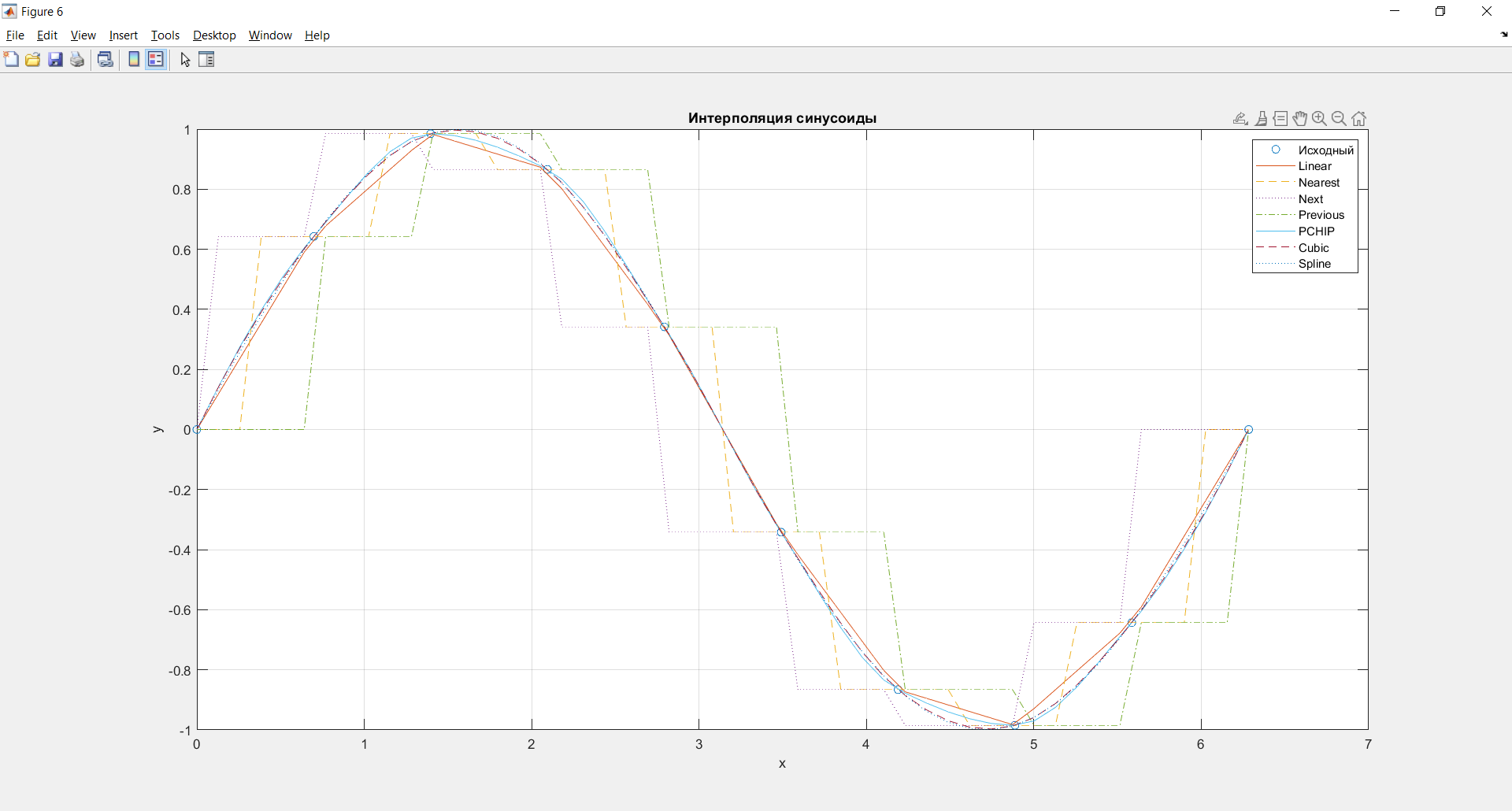
Рисунок 10 – Интерполяция синусоиды

Вывод:

В ходе выполнения лабораторной работы были изучены основные функции для работы с многочленами, включая нахождение их корней, вычисление коэффициентов, а также применение операций умножения, деления и дифференцирования. Освоены методы аппроксимации и интерполяции данных, позволяющие с высокой точностью приближать экспериментальные зависимости и восстанавливать значения на новых сетках. Эти навыки полезны для анализа и обработки данных в инженерных и научных задачах.