matlab laboratornye / матлаботчет5

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра РС

отчет

по лабораторной работе №5

по дисциплине «MATLAB»

Тема: РАБОТА С ФУНКЦИЯМИ В MATLAB

Студент гр. фыв		фыв
Преподаватель		фыв

Санкт-Петербург

фыв

Цель работы.

Знакомство с принципами работы с несколькими стандартными функциями; освоение принципов создания функций пользователя.

Основные теоретические сведения.

1. Вычисление определенного интеграла. Для численного интегрирования используется функция quad. Формат функции: quad(F,<нижний предел интегрирования>,<верхний предел интегрирования>,<погрешность>).

2. Для вычисления локального минимума функции в интервале (x₁,x₂) используется функция x_min = fminbnd(‘«имя функции»‘,x₁,x₂).

3. Для нахождения нулей функции одной переменной в окрестности точки x₀ используется функция z = fzero(‘«имя функции»‘,x₀). 4. Пусть имеется функция f(x), не являющаяся стандартной в системе MatLab.

Пользователю необходимо сделать так, чтобы эта функция стала

доступной в системе MatLab, как и стандартные функции, т. е.

чтобы у функции было определенное имя, по которому ее можно быстро вызвать, определить корни этой функции, ее минимум, максимум, вычислить определенный интеграл от этой функции и т. п., т.е. использовать ее как основу для работы стандартных MatLab функций.

Для задания функции пользователя создается m-файл, первая

строка которого имеет формат: function <выходные переменные> = <имя функции> (<входные переменные>).

Выходные и входные переменные могут и отсутствовать.

Имя m-файла с функцией пользователя обязательно должно совпадать с именем реализованной в нем функции.

Копии рабочего поля.

Вычисление определенного интеграла .

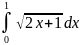Рисунок 1 - Вычисление интеграла

Вызванная функция quad, позволяющая вычислить интеграл, с её аргументами: 'sqrt(2*x+1)' – функция, интеграл которой требуется посчитать, 0 – нижняя граница, 1 – верхняя граница. Функцию quad можно присвоить переменной z для более удобного использования. С той же целью переменной F присвоено 'sqrt(2*x+1)'.

Рисунок 2 - Нахождение корня функции и минимума функции.

Функция fzero позволяет найти корень функции 'sin' – первого аргумента относительно близ лежащей точки x₀ - второго аргумента, в случае синусоиды ближайший корень к 3 – это 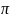. Функция fminbnd задается следующими аргументами: 'cos' – функция, на отрезке которой ищется минимальное значение, 3 и 4 – точки, обозначающие начало и конец интервала поиска экстремума.

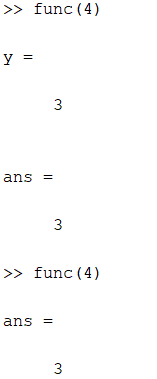
Рисунок 3 - Вызов исходного и измененного m-файла func.

Для того, чтобы при вызове m-файла не выводился результат переменной y, а только результат кода файла, в конце второй строки функции нужно поставить символ «;».

Чтобы вычислить интеграл , нужно создать пользовательскую функцию, выходными параметрами которой будет y, а входных параметров не будет, так как вычисление интеграла не требует их. После вызова пользовательской функции будет выведен ответ, который был получен ранее во время работы с рабочей областью.

Рисунок 4 - Результат вычисления интеграла с помощью m-файла.

Содержание m-файла.

Исходный код:

Измененный код:

Вычисление интеграла с помощью m-файла:

Вывод.

Были освоены навыки вычисления интеграла, нахождения корней и экстремума функции пользователя, которые могут пригодиться для работы с сложными функциями и графиками, а также упростят процесс полного исследования функции. Выполнен процесс задания функции пользователя в m-файле и её реализации в рабочей области.