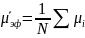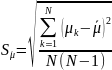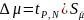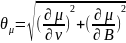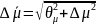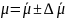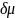Лабораторочки 3 семестр (не фкти) / 16 / 16обработка

Обработка лабораторной работы №16.

h = 6,63 * 10^-34 Дж*с

μ_Б = 9,27 * 10^-24 А*м²

n = 200 витков

R = 0,0927 м

1. Найдем B_i, используя I_i и параметры колец Гемгольца:

I, A		0,7	0,6	0,5	0,4	0,3	0,2
+ -	B, мТл	1,344	1,152	0,96	0,768	0,576	0,384
- +		1,344	1,152	0,96	0,768	0,576	0,384

2. Рассчитаем эффективный магнитный момент μ_эф молекулы ДФПГ, найдя среднее значение и доверительную погрешность:

;

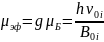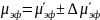
А*м2		А*м2
1,58 * 10-23	2,3 * 10-24	5,06 * 10-24

А*м2	А*м2	А*м2	%
1,32 * 10-29	5,06 * 10-24	(1,58 ± 0,51) * 10-23	32,1

3. Рассчитаем фактор Ланде g, используя магнетон Бора μ_Б:

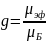
g = 1,704

Каждая молекула ДФПГ имеет сильно делокализованный неспаренный электрон, для которого L ≈ 0. При L = 0 вытекает, что J = S. Отсюда следует, что значение должно быть g = 2. Отклонение, предположительно, связано с неточным снятием показаний. В ином случае, в момент снятия показаний у электрона наблюдалось одновременное спиновое и орбитальное движение.

4. Рассчитаем энергетическую ширину δE:

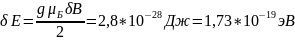
Оценим время жизни молекулы ДФПГ в возбужденном состоянии, используя соотношение неопределенностей Гейзенберга−Бора:

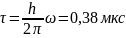
5. Построим на одном графике зависимости резонансной частоты ν0 от

индукции поля В₀ катушек для прямого и обратного их включения.

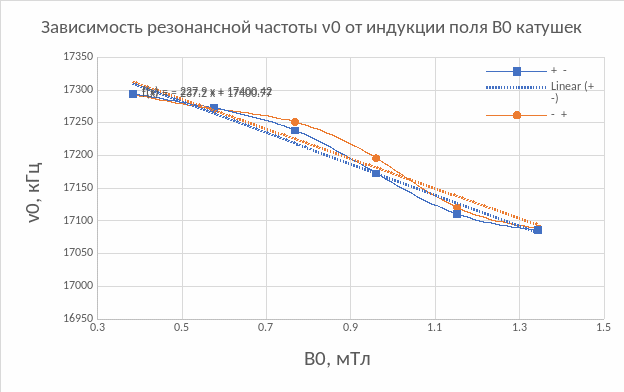
В_Л(+ -) = 73,4 мТл

В_Л(- +) = 76,4 мТл

Вывод: в ходе лабораторной работы были вычислены значения индукции магнитного поля колец Гемгольца при разных значения входного тока. Рассчитана экспериментальная величина магнитного эффективного момента 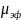= (1,58 ± 0,51) * 10^-23 А*м². Теоретическая равна = 1,85 * 10^-23 А*м². Экспериментальная фактор Ланде g = 1,7 отличается от теоретического g = 2. 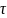Время жизни молекулы ДФПГ в возбужденном состоянии = 0,38 мкс. Построена зависимость резонансной частоты v₀ от индукции магнитного поля B₀.