РГР №1 по электротехнике

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра электротехники предприятий

Расчетно-графическая работа №1

Расчет цепей постоянного тока

Вариант №10

Выполнила ст.гр. БГР-13-02 Зарипова Н.Р.

Проверила Рябишина Л.А.

Приняла Рябишина Л.А.

Уфа 2014

ЦЕЛЬ РАБОТЫ:

1. Для заданной разветвленной электрической цепи постоянного тока выполнить расчеты различными методами:

• Методом с помощью законов Ома и Кирхгофа;

• Методом контурных токов;

• Методом наложения.

2. Проверить результаты расчетов составлением баланса мощностей.

3. Построить потенциальную диаграмму для внешнего контура цепи.

ЗАДАНИЕ:

Параметры цепи	E1	E2	R1	R2	R3	R4	R5
Вариант задания Номер схемы	В	В	Ом	Ом	Ом	Ом	Ом
10	50	70	7	50	5	20	25

РЕШЕНИЕ.

1. Решаем методом с применением законов Ома и Кирхгофа.

Выберем направления токов в ветвях и обозначим их на схеме цепи.

Определяем число ветвей и узлов:

y = 3;

b = 5;

3 независимых контура.

По первому закону Кирхгофа:

у – 1 = 3 – 1 = 2 уравнения;

- I₁ + I₃ – I₄ = 0

I₂ – I₃ + I₅ = 0

По второму закону Кирхгофа: b – y + 1 = 5 – 3 + 1 = 3 уравнения;

R₁I₁ – R₄I₄ = -ε₁

R₃I₃ + R₄I₄ + R₅I₅ = 0

R₂I₂ – R₅I₅ = ε₂

Перепишем систему уравнений в матричном виде и решим его методом Гаусса

	-1	0	1	-1	0	0
	0	1	-1	0	1	0
	7	0	0	-20	0	-50
	0	0	5	20	25	0
	0	50	0	0	-25	70

1-ую строку делим на -1

	1	0	-1	1	0	0
	0	1	-1	0	1	0
	7	0	0	-20	0	-50
	0	0	5	20	25	0
	0	50	0	0	-25	70

от 3 строк отнимаем 1 строку, умноженную соответственно на 7

	1	0	-1	1	0	0
	0	1	-1	0	1	0
	0	0	7	-27	0	-50
	0	0	5	20	25	0
	0	50	0	0	-25	70

от 5 строк отнимаем 2 строку, умноженную соответственно на 50

	1	0	-1	1	0	0
	0	1	-1	0	1	0
	0	0	7	-27	0	-50
	0	0	5	20	25	0
	0	0	50	0	-75	70

3-ую строку делим на 7

	1	0	-1	1	0	0
	0	1	-1	0	1	0
	0	0	1	-27/7	0	-50/7
	0	0	5	20	25	0
	0	0	50	0	-75	70

от 1; 2; 4; 5 строк отнимаем 3 строку, умноженную соответственно на -1; -1; 5; 50

	1	0	0	-20/7	0	-50/7
	0	1	0	-27/7	1	-50/7
	0	0	1	-27/7	0	-50/7
	0	0	0	275/7	25	250/7
	0	0	0	1350/7	-75	2990/7

4-ую строку делим на 275/7

	1	0	0	-20/7	0	-50/7
	0	1	0	-27/7	1	-50/7
	0	0	1	-27/7	0	-50/7
	0	0	0	1	7/11	10/11
	0	0	0	1350/7	-75	2990/7

от 1; 2; 3; 5 строк отнимаем 4 строку, умноженную соответственно на -20/7; -27/7; -27/7; 1350/7

	1	0	0	0	20/11	-50/11
	0	1	0	0	38/11	-40/11
	0	0	1	0	27/11	-40/11
	0	0	0	1	7/11	10/11
	0	0	0	0	-2175/11	2770/11

5-ую строку делим на -2175/11

	1	0	0	0	20/11	-50/11
	0	1	0	0	38/11	-40/11
	0	0	1	0	27/11	-40/11
	0	0	0	1	7/11	10/11
	0	0	0	0	1	-554/435

от 1; 2; 3; 4 строк отнимаем 5 строку, умноженную соответственно на 20/11; 38/11; 27/11; 7/11

	1	0	0	0	0	-194/87
	0	1	0	0	0	332/435
	0	0	1	0	0	-74/145
	0	0	0	1	0	748/435
	0	0	0	0	1	-554/435

Ответ:

	I1 = -194/87 = -2,2298 А
	I2 = 332/435 = 0,7632 А
	I3 = -74/145 = -0,5103 А
	I4 = 748/435 = 1,7195 А
	I5 = -554/435 = -1,2735 А

2. Решаем методом контурных токов.

Обозначим на схеме направление контурных токов (чаще всего их направление совпадает с направлением обхода контура).

Запишем второй закон Кирхгофа для каждого контура и составим систему:

Составляем матрицу:

	27	-20	0	-50
	-20	50	-25	0
	0	-25	75	70

1-ую строку делим на 27

	1	-20/27	0	-50/27
	-20	50	-25	0
	0	-25	75	70

от 2 строк отнимаем 1 строку, умноженную соответственно на -20

	1	-20/27	0	-50/27
	0	950/27	-25	-1000/27
	0	-25	75	70

2-ую строку делим на 950/27

	1	-20/27	0	-50/27
	0	1	-27/38	-20/19
	0	-25	75	70

от 1; 3 строк отнимаем 2 строку, умноженную соответственно на -20/27; -25

	1	0	-10/19	-50/19
	0	1	-27/38	-20/19
	0	0	2175/38	830/19

3-ую строку делим на 2175/38

	1	0	-10/19	-50/19
	0	1	-27/38	-20/19
	0	0	1	332/435

от 1; 2 строк отнимаем 3 строку, умноженную соответственно на -10/19; -27/38

	1	0	0	-194/87
	0	1	0	-74/145
	0	0	1	332/435

Ответ:

	II= -194/87 = -2.2298 А
	III = -74/145 = -0,5103 А
	IIII = 332/435 = 0,7632 А

Находим реальные токи:

I₁ = I_I = -2.2298 A

I₂ = I_III = 0.7632 A

I₃ = I_II = -0.5103 A

I₄ = I_II – I_I = 1.7195 A

I₅ = I_II – I_III = -1.2735 A

3. Решаем методом наложения.

1. Зануляем ЭДС ε₂, преобразовываем схему при помощи эквивалентных преобразований.

Расставляем частичные токи.

2. Рассчитываем полное сопротивление (общее и эквивалентное):

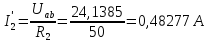
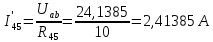
3. Зануляем теперь ЭДС ε₁ и проделываем то же самое:

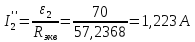
4. Найдем реальные токи:

По первому и второму закону Кирхгофа найдем теперь I₃, I₄ и I₅:

- I₁ + I₃ – I₄ = 0

I₂ – I₃ + I₅ = 0

R₁I₁ – R₄I₄ = -ε₁

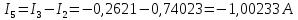
Таким образом, токи у нас получились примерно такие же, как и в предыдущим двух методах, но с небольшой погрешностью.