2.3. Метод Петрика

Метод Петрика позволяет исключить процедуру построения и анализа таблицы меток. После получения всех первичных импликант, для каждого минитерма строится дизъюнкция из тех импликант, которые входят в данный минитерм. Затем все дизъюнкции логически перемножаются, раскрываются скобки, выполняются все поглощения, т. е. получается некоторая ДНФ. При этом, каждая конъюнкция, входящая в ДНФ, соответствует одной из тупиковых ДНФ. Выбирается самая короткая, которая соответствует МДНФ.

Пример

Минитермы 4-го ранга

Минитермы 3-го ранга

Минитермы 2-го ранга

Простые импликанты

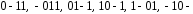
Записываем дизъюнкции из простых импликант, которые для простоты обозначим:

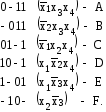
В минитермы входят импликанты:

Записываем конъюнкцию из этих дизъюнкций и выполняем операции поглощения

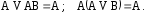
и перемножаем скобки.

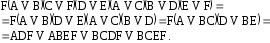
Получили 4 тупиковых ДНФ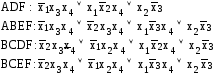

Минимальной является первая, т. е. МДНФ имеет вид:

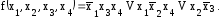
2.4. Метод Блека - Порецкого

Недостатком рассмотренных методов является то, что сокращенная ДНФ строится по СДНФ, которая при n= 5, 6 становится довольно громоздкой. Например, если функция имеет следующий вид ДНФ:

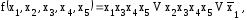
и требуется определить для нее МДНФ, нужно построить СДНФ, которая состоит из 18 минитермов.

Метод Блека - Порецкого позволяет строить Сокр. ДНФ не по СДНФ, а по произвольной ДНФ. Метод основан на следующей теореме.

Теорема

Если в ДНФ функции 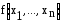входят две конъюнкции вида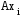и, то имеет место равенство:

(*)

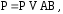где P– ДНФ функции.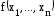

Для построения Сокр. ДНФ по произвольной ДНФ исходную ДНФ следует дополнить новыми членами по правилу (*), затем выполнить операцию поглощения, затем снова дополнить и снова выполнить поглощение и т. д., до тех пор, пока это возможно. Получив Сокр. ДНФ, можно воспользоваться для получения МДНФ методом Квайна - Мак - Класки или Петрика.

Пример

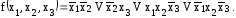
Пары, удовлетворяющие теореме

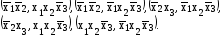
Дополняем исходную ДНФ

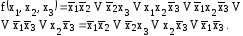
Здесь есть одна пара, удовлетворяющая условию теоремы 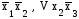, но она ничего не добавляет, т. е. мы получили Сокр. ДНФ.

Далее по методу Квайна строим таблицу меток

	000	001	101	110	010
00-	1	1
-01		1	1
-10				1	1
0-0	1				1

Существенные импликанты -01, -10.

Здесь две МДНФ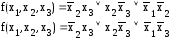

Замечание.

Проблема минимизации функций может быть сформулирована и решена в других базисах, например, 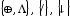. Для этих базисов разработаны методы минимизации.

ЛИТЕРАТУРА

1. Мендельсон Э. Введение в математическую логику. – М. : Наука, 1984.

2. Марков А.А. Элементы математической логики. – М.: Изд-во МГУ, 1984.

3. Колмогоров А.Н., Драгалин А.Г. Введение в математическую логику: учебное пособие. – М. : Изд-во Моск. ун-та, 1982.

4. Ершов Ю.Л., Палютин Е.А. Математическая логика: (Уч. пособие для ВУЗов). – М.: Наука, 1979.

5. Новиков П.С. Элементы математической логики – М. : Наука,1973.