
- •Методические указания к лабораторной работе характеристики детерминированныхсигналов Дисциплина «Элементы общей теории сигналов»
- •Характеристики детерминированныхсигналов
- •1 Краткие теоретические сведения
- •1.2. Спектральные характеристики непериодических сигналов
- •1.3. Энергетические характеристики сигналов
- •2 Задания к лабораторной работе
- •2.1 Спектральные характеристики периодических сигналов
- •2.2. Спектральные характеристики непериодических сигналов
- •2.3 Энергетические характеристики сигналов
- •4 Техника безопасности
- •Действия сотрудников и студентов в случае пожара
- •5 Контрольные вопросы
- •Список использованных источников
Министерство образования и науки Российской Федерации
Филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования
«Уфимский государственный нефтяной технический университет» в г. Салавате
Кафедра «Электрооборудование и автоматика промышленных предприятий»
СОГЛАСОВАНО УТВЕРЖДАЮ
Зав. кафедрой ЭАПП, профессор Зам. директора по учебной работе, доцент
_______________М.Г. Баширов ______________________Н.Н. Лунева
_______________2014 __________________2014
Методические указания к лабораторной работе характеристики детерминированныхсигналов Дисциплина «Элементы общей теории сигналов»
СОГЛАСОВАНО РАЗРАБОТАЛИ
Инженер по охране труда Доцент кафедры ЭАПП
___________ Г.В. Мангуткина ________ А.С. Хисматуллин
____________2014 _____________2014
студент гр. БАТ-11-21
_________Е.И.Буланкин
_____________2014
Салават
2014
Методические указания предназначены для студентов направления подготовки 220700 «Автоматизация технологических процессов и производств», профиль «Автоматизация технологических процессов и производств в нефтехимии и нефтепереработке»
Обсуждено на заседании кафедры ЭАПП
Протокол № ______ от ___________________2014
Филиал ФГБОУ ВПО УГНТУ в г.Салавате, 2014
Характеристики детерминированныхсигналов
Цель работы: изучение характеристик детерминированных сигналов в программе «Mathcad».
1 Краткие теоретические сведения
Спектральные характеристики периодических сигналов
Условие периодичности – x(t) = x(t+mT), где T – период, m – натуральное число, m = 1, 2, .... Любой периодический сигнал x(t) может быть представлен тригонометрическим рядом Фурье.
x(t) = a0 + ∑ (ak coskw1t + bk sinkw1t) = a0 + ∑ Ak cos(kw1t + φk), (1.1)
где ω1 = 2π/T – угловая частота 1-й или основной гармоники; a0, аk , и bк коэффициенты разложения, вычисляемые по формулам:
a0
=
 ak
=
ak
=
 bk
=
bk
=


где Ak – амплитуда k-й гармоники;φk – фаза k-й гармоники;a0 – среднее значение сигнала (постоянная составляющая);kω1= ωk – угловая частотаk-й гармоники;tн– момент времени, соответствующий началу периода.
Зависимости Akиφkот частоты ωk – это спектры амплитуд и фаз соответственно.
В некоторых случаях более удобна комплексная форма ряда Фурье
 (1.2)
(1.2)
Коэффициенты
 ряда (1.2) вычисляются по формуле
ряда (1.2) вычисляются по формуле
 (1.3)
(1.3)
Формулы
(1.2) и (1.3) – пара преобразований Фурье.
Совокупность коэффициентов
 комплексный спектр периодического
сигнала x(t).Совокупность
действительных величин
комплексный спектр периодического
сигнала x(t).Совокупность
действительных величин
 в зависимости
от частоты – спектр
амплитуд.
Совокупность величин φk
в зависимости
от частоты – спектр
фаз.
в зависимости
от частоты – спектр
амплитуд.
Совокупность величин φk
в зависимости
от частоты – спектр
фаз.
Ряд (1.2) удобно представлять в форме
 (1.4)
(1.4)
 (1.5)
(1.5)
Пример 1.1
Построить спектры амплитуд и фаз сигнала x(t), аналитическое выражение которого при исходных данных Vm:= 4volt∙sec-1,T:= 2secиt0:= 2secимеет вид
 .
.
График
сигнала при диапазоне изменения времени
t:=-1.5∙T, представлен на рисунке 1.
представлен на рисунке 1.

Рисунок 1 – График сигнала
Решение
Так как данный сигнал – периодическая функция времени, то для его спектрального представления нужно использовать или тригонометрический или комплексный ряд Фурье. Найдем спектры амплитуд и фаз на основе тригонометрического ряда Фурье.
Определим
коэффициенты разложения сигнала на
интервале t:= 0..Tпри угловой частоте основной гармоники
ω1:= и числе гармоникk:= 1..5.
и числе гармоникk:= 1..5.
Постоянная составляющая

Косинусоидальный коэффициент

Подстановка численных значений Vm, T и ω1дает

В результате интегрирования получим

Например, a1 = 0 volt; a2 = 0 volt; a3 = 0 volt; a4 = 0 volt.
Более удобна другая форма определения коэффициентов разложения.
Так как

то выражая t0 и ω1 через T, имеем


Отсюда следует, что при k>0 коэффициенты ak равны нулю.
Cинусоидальный коэффициент

Выражая t0 и ω1 через T, можно получить


Отсюда после упрощений следует

Амплитуда k-й гармоники
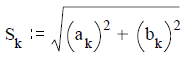
при k>1 будет
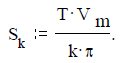
Таким образом, с учетом постоянной составляющей амплитудный спектр

Фазовый спектр
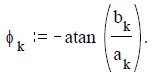
Так как коэффициенты ak=0 и bk<0, и составит, например для k=1, φ = 1.571.
Графики данных спектров в виде столбчатых диаграмм приведены на рисунке 2.

