1

  ЗАДАНИЕ N 1 сообщить об ошибке Тема: Второе начало термодинамики. Энтропия В идеальной тепловой машине из каждого  теплоты, получаемого от нагревателя,  отдается холодильнику. Если температура холодильника 27°С, то температура нагревателя (в °С) равна …

			127
			400
			200
			225

Решение: Коэффициент полезного действия тепловой машины определяется соотношением , где  и  – количество теплоты, полученное от нагревателя и отданное холодильнику соответственно. Для идеальной тепловой машины  ( и  – температура нагревателя и холодильника соответственно). Приравнивая правые части этих выражений, получаем . Отсюда .

  ЗАДАНИЕ N 2 сообщить об ошибке Тема: Средняя энергия молекул Кинетическая энергия (в Дж) всех молекул в 2 г неона при температуре 300 К равна …

Решение: Средняя кинетическая энергия одной молекулы равна , где  – постоянная Больцмана, – термодинамическая температура,  – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы . Молекула неона имеет 3 поступательные степени свободы, следовательно, . В 2 г неона содержится  молекул, где масса газа, молярная масса неона, число Авогадро. Кинетическая энергия всех молекул будет равна: 

  ЗАДАНИЕ N 3 сообщить об ошибке Тема: Распределения Максвелла и Больцмана На рисунке представлены графики зависимости концентрации молекул идеального газа  от высоты  над уровнем  моря для двух разных температур –   (распределение Больцмана). Для графиков этих функций верными являются утверждения, что …

			температура  выше температуры
			концентрация молекул газа на «нулевом уровне»  с повышением  температуры уменьшается
			температура  ниже температуры
			концентрация молекул газа на «нулевом уровне»  с повышением температуры увеличивается

Решение: Зависимость концентрации молекул идеального газа от высоты  для некоторой температуры  определяется распределением Больцмана: , где  концентрация молекул на высоте , масса молекулы,  ускорение свободного падения,  постоянная Больцмана. Из формулы следует, что при постоянной температуре концентрация газа больше там, где меньше потенциальная энергия его молекул , и уменьшается с высотой по экспоненциальному закону тем медленнее, чем больше температура: . С повышением температуры из-за увеличения энергии хаотического теплового движения молекулы более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне»  уменьшается, а на высоте  увеличивается.

  ЗАДАНИЕ N 4 сообщить об ошибке Тема: Первое начало термодинамики. Работа при изопроцессах Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке. Работа газа за цикл (в кДж) равна …

5 |

Решение: Работу газа в циклическом процессе можно найти, определив площадь, ограниченную кривой цикла в координатах  Цикл имеет форму трапеции. Тогда 

  ЗАДАНИЕ N 5 сообщить об ошибке Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга Если протон и -частица прошли одинаковую ускоряющую разность потенциалов, то отношение их длин волн де Бройля равно …

			4
			2

Решение: -частица – это ядро атома гелия, состоящее из двух протонов и двух нейтронов. Длина волны де Бройля определяется по формуле , где p – импульс частицы. Импульс частицы можно выразить через ее кинетическую энергию: . По теореме о кинетической энергии, согласно которой работа сил электрического поля идет на приращение кинетической энергии, . Отсюда можно найти , полагая, что первоначально частица покоилась:  Окончательное выражение  для длины волны де Бройля через ускоряющую разность потенциалов имеет вид:  Учитывая, что  и  отношение длин волн де Бройля протона и -частица равно: 

 ЗАДАНИЕ N 6 сообщить об ошибке Тема: Уравнение Шредингера (конкретные ситуации) Момент импульса электрона в атоме и его пространственные ориентации могут быть условно изображены векторной схемой, на которой длина вектора пропорциональна модулю орбитального момента импульса  электрона. На рисунке приведены возможные ориентации вектора . Значение орбитального квантового числа для указанного состояния равно …

			2
			1
			4
			5

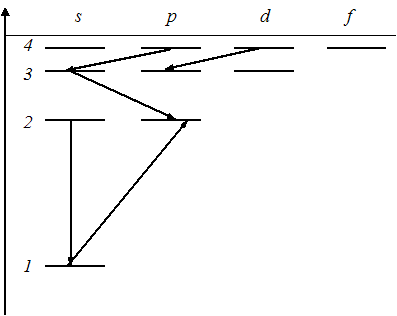
  ЗАДАНИЕ N 7 сообщить об ошибке Тема: Спектр атома водорода. Правило отбора Закон сохранения момента импульса накладывает ограничения на возможные переходы электрона в атоме с одного уровня на другой (правило отбора). В энергетическом спектре атома водорода (см. рис.) запрещенным является переход …

Решение: Для орбитального квантового числа l существует правило отбора . Это означает, что возможны только такие переходы, в которых l изменяется на единицу. Поэтому запрещенным переходом является переход , так как в этом случае .

 ЗАДАНИЕ N 8 сообщить об ошибке Тема: Уравнения Шредингера (общие свойства) Стационарное уравнение Шредингера имеет вид . Это уравнение описывает …

			электрон в водородоподобном атоме
			движение свободной частицы
			электрон в трехмерном потенциальном ящике
			линейный гармонический осциллятор

  ЗАДАНИЕ N 9 сообщить об ошибке Тема: Сложение гармонических колебаний Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудами  Установите соответствие междуразностью фаз складываемых колебаний и амплитудой результирующего колебания. 1.  2.  3. 0

1
2
3

Решение: Амплитуда результирующего колебания, полученного при сложении двух гармонических колебаний одного направления с одинаковыми частотами, определяется по формуле , где и  – амплитуды, () – разность фаз складываемых колебаний. Если разность фаз , , то  и . Если  , то   Если  , то .

  ЗАДАНИЕ N 10 сообщить об ошибке Тема: Свободные и вынужденные колебания Маятник совершает вынужденные колебания со слабым коэффициентом затухания , которые подчиняются дифференциальному уравнению  Амплитуда колебаний будет максимальна, если частоту вынуждающей силы уменьшить в _____ раз(-а).

5 |

Решение: Дифференциальное уравнение вынужденных колебаний имеет вид , где коэффициент затухания,  собственная круговая частота колебаний; амплитудное значение вынуждающей силы, деленное на массу; частота вынуждающей силы. При слабом затухании (коэффициент затухания значительно меньше собственной частоты колебаний маятника) амплитуда колебаний будет максимальна, если частота вынуждающей силы совпадет с собственной частотой колебаний маятника (явление резонанса). Собственная частота колебаний равна: , частота вынуждающей силы . Следовательно, частоту вынуждающей силы необходимо уменьшить в 5 раз.

 ЗАДАНИЕ N 11 сообщить об ошибке Тема: Волны. Уравнение волны Уравнение бегущей волны имеет вид: , где  выражено в миллиметрах,  – в секундах,  – в метрах. Отношение амплитудного значения скорости частиц среды к скорости распространения волны равно …

			0,028
			28
			0,036
			36

  ЗАДАНИЕ N 12 сообщить об ошибке Тема: Энергия волны. Перенос энергии волной В упругой среде плотностью распространяется плоская синусоидальная волна. Если амплитуда волны увеличится в 4 раза, а частота в 2 раза, то плотность потока энергии (вектор Умова) увеличится в ______ раз(-а).

64 |

Решение: Плотность потока энергии, то есть количество энергии, переносимой волной за единицу времени через единицу площади площадки, расположенной перпендикулярно направлению переноса энергии, равна:  где – объемная плотность энергии, – скорость переноса энергии волной (для синусоидальной волны эта скорость равна фазовой скорости). Среднее значение объемной плотности энергии равно:  где – амплитуда волны,  – частота. Следовательно, плотность потока энергии увеличится в 64 раза.

 ЗАДАНИЕ N 13 сообщить об ошибке Тема: Тепловое излучение. Фотоэффект На рисунке приведены две вольтамперные характеристики вакуумного фотоэлемента. Если – освещенность фотоэлемента,  частота падающего на него света, то … 

			;
			;
			;
			;

 ЗАДАНИЕ N 14 сообщить об ошибке Тема: Поляризация и дисперсия света Угол между плоскостями пропускания двух поляризаторов равен . Если угол увеличить в 2 раза, то интенсивность света, прошедшего через оба поляризатора …

			станет равной нулю
			увеличится в 2 раза
			уменьшится в 2 раза
			уменьшится в 4 раза

  ЗАДАНИЕ N 15 сообщить об ошибке Тема: Интерференция и дифракция света Плосковыпуклая линза выпуклой стороной лежит на стеклянной пластинке (установка для наблюдения колец Ньютона). Если на плоскую поверхность линзы падает нормально свет с длиной волны 0,6 мкм, то толщина воздушного зазора (в нм) в том месте, где в отраженном свете видно первое темное кольцо, равна …