4

 ЗАДАНИЕ N 1 сообщить об ошибке Тема: Волны. Уравнение волны На рисунке представлена мгновенная фотография электрической составляющей электромагнитной волны, переходящей из среды 1 в среду 2 перпендикулярно границе раздела сред АВ. Отношение скорости света в среде 2 к его скорости в среде 1 равно …

			1,5
			0,67
			1,7
			0,59

  ЗАДАНИЕ N 2 сообщить об ошибке Тема: Свободные и вынужденные колебания Амплитуда затухающих колебаний уменьшилась в  раз ( – основание натурального логарифма) за . Коэффициент затухания (в ) равен …

20 |

Решение: Амплитуда затухающих колебаний изменяется со временем по закону , где – коэффициент затухания. По условию . Тогда  и .

 ЗАДАНИЕ N 3 сообщить об ошибке Тема: Энергия волны. Перенос энергии волной В упругой среде плотностью распространяется плоская синусоидальная волна с частотой  и амплитудой  При переходе волны в другую среду, плотность которой в 2 раза меньше, амплитуду увеличивают в 4 раза, тогда объемная плотность энергии, переносимой волной, увеличится в ____ раз(-а).

8

  ЗАДАНИЕ N 4 сообщить об ошибке Тема: Сложение гармонических колебаний Складываются два гармонических колебания одного направления с одинаковыми частотами и амплитудами, равными  и . Установите соответствие между разностью фаз складываемых колебаний и амплитудой результирующего колебания. 1. 0 2.  3. 

1
2
3

Решение: Амплитуда результирующего колебания, полученного при сложении двух гармонических колебаний одного направления с одинаковыми частотами, определяется по формуле , где и  – амплитуды, () – разность фаз складываемых колебаний. Если разность фаз , , то  и . Этот результат можно было получить сразу: при разности фаз  векторы  и  сонаправлены, и длина результирующего вектора  равна сумме длин складываемых векторов. Если  , то  и . Если  , то  и .

  ЗАДАНИЕ N 5 сообщить об ошибке Тема: Явление электромагнитной индукции На рисунке представлена зависимость магнитного потока, пронизывающего некоторый контур, от времени: График зависимости ЭДС индукции в контуре от времени представлен на рисунке …

Решение: В соответствии с законом Фарадея для электромагнитной индукции электродвижущая сила индукции в замкнутом проводящем контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром: . Следовательно, если магнитный поток увеличивается со временем по линейному закону в интервале 0 – 0,1 с, то ЭДС индукции будет равна отрицательной постоянной величине; если не изменяется в интервале 0,1 – 0,3 с, то ЭДС индукции равна нулю; если убывает по линейному закону в интервале 0,3 – 0,4 с, то ЭДС индукции будет равна положительной постоянной величине.

 ЗАДАНИЕ N 6 сообщить об ошибке Тема: Электрические и магнитные свойства вещества Неверным для ферромагнетиков является утверждение …

			Магнитная проницаемость ферромагнетика – постоянная величина, характеризующая его магнитные свойства.
			Ферромагнетиками называются твердые вещества, которые могут обладать спонтанной намагниченностью, то есть могут быть намагничены в отсутствие внешнего магнитного поля.
			Для ферромагнетиков характерно явление магнитного гистерезиса: связь между магнитной индукцией (намагниченностью) и напряженностью внешнего магнитного поля оказывается неоднозначной и определяется предшествующей историей намагничивания ферромагнетика.
			Для каждого ферромагнетика имеется температура, называемая температурой или точкой Кюри, при которой ферромагнитные свойства исчезают.

  ЗАДАНИЕ N 7 сообщить об ошибке Тема: Уравнения Максвелла Физический смысл уравнения Максвелла  заключается в следующем …

			изменяющееся со временем магнитное поле порождает вихревое электрическое поле
			источником вихревого магнитного поля помимо токов проводимости является изменяющееся со временем электрическое поле
			«магнитных зарядов» не существует: силовые линии магнитного поля замкнуты
			источником электрического поля являются свободные электрические заряды

Решение: Уравнение Максвелла  означает, что с переменным магнитным полем неразрывно связано вихревое электрическое поле.

  ЗАДАНИЕ N 8 сообщить об ошибке Тема: Законы постоянного тока Два одинаковых источника тока соединены последовательно. Если источники соединить параллельно, то сила тока короткого замыкания …

			увеличится в 2 раза
			увеличится в 4 раза
			не изменится
			уменьшится в 2 раза

Решение: Сила тока короткого замыкания , где  и  – ЭДС и внутреннее сопротивление батареи, состоящей из двух источников. При последовательном соединении источников , ; здесь  и  – ЭДС и внутреннее сопротивление одного источника. При параллельном соединении , а . Тогда , .

  ЗАДАНИЕ N 9 сообщить об ошибке Тема: Магнитостатика Небольшой контур с током I помещен в неоднородное магнитное поле с индукцией . Плоскость контура перпендикулярна плоскости чертежа, но не перпендикулярна линиям индукции. Под действием поля контур …

			повернется по часовой стрелке и сместится вправо
			повернется против часовой стрелки и сместится вправо
			повернется против часовой стрелки и сместится влево
			повернется по часовой стрелке и сместится влево

Решение: На контур с током в однородном магнитном поле действует вращающий момент , стремящийся расположить контур таким образом, чтобы вектор его магнитного момента  был сонаправлен с вектором магнитной индукции  поля. Если контур с током находится в неоднородном магнитном поле, то на него действует еще и результирующая сила, под действием которой незакрепленный контур втягивается в область более сильного поля, если угол между векторами  и  острый (α < 90°). Если же указанный угол тупой (α > 90°), то контур с током выталкивается в область более слабого поля, поворачивается под действием вращающего момента, так что угол становится острым, и затем втягивается в область более сильного поля. В соответствии с этим контур повернется по часовой стрелке и сместится вправо.

 ЗАДАНИЕ N 10 сообщить об ошибке Тема: Электростатическое поле в вакууме Электростатическое поле создано двумя точечными зарядами:  и .  Отношение потенциала поля, созданного вторым зарядом в точке А, к потенциалу результирующего поля в этой точке равно …

4

  ЗАДАНИЕ N 11 сообщить об ошибке Тема: Уравнения Шредингера (общие свойства) Верным для уравнения Шредингера , где = const является утверждение:

			Уравнение характеризует движение микрочастицы в области пространства, где потенциальная энергия – постоянная величина.
			Уравнение соответствует трехмерному случаю.
			Уравнение является нестационарным.
			Уравнение описывает линейный гармонический осциллятор.

Решение: Уравнение стационарно, так как волновая функция  не зависит от времени (отсутствует производная по времени). Стационарное уравнение Шредингера в общем случае имеет вид: . Здесь  потенциальная энергия микрочастицы. По условию  const. Для гармонического осциллятора . Поэтому из приведенных утверждений верным является следующее: «Уравнение характеризует движение микрочастицы в области пространства, где потенциальная энергия – постоянная величина».

  ЗАДАНИЕ N 12 сообщить об ошибке Тема: Спектр атома водорода. Правило отбора На рисунке дана схема энергетических уровней атома водорода.  Наибольшая длина волны спектральной линии (в нм) серии Лаймана равна … (h = 6,63·10^-34 Дж·с)

			122
			92
			661
			368

Решение: Серию Лаймана дают переходы в состояние с n = 1. Учитывая связь длины волны и частоты  и правило частот Бора , можно сделать вывод о том, что линии с наибольшей длиной волны (то есть с наименьшей частотой) в серии Лаймана соответствует переход со второго энергетического уровня. Тогда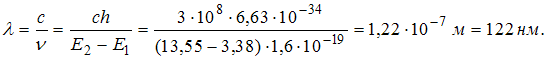 

 ЗАДАНИЕ N 13 сообщить об ошибке Тема: Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга Время жизни атома в возбужденном состоянии 10 нс. Учитывая, что постоянная Планка , ширина энергетического уровня (в эВ) составляет не менее …

 ЗАДАНИЕ N 14 сообщить об ошибке Тема: Уравнение Шредингера (конкретные ситуации) На рисунках схематически представлены графики распределения плотности вероятности обнаружения электрона по ширине одномерного потенциального ящика с бесконечно высокими стенками для состояний с различными значениями главного квантового числа n. В состоянии с n = 3 вероятность обнаружить электрон в интервале от  до  равна …

  ЗАДАНИЕ N 15 сообщить об ошибке Тема: Второе начало термодинамики. Энтропия На рисунке изображен цикл Карно в координатах (T, S), где S – энтропия. Адиабатное сжатие происходит на этапе …

			4 – 1
			2 – 3
			1 – 2
			3 – 4

Решение: Адиабатные процессы происходят без теплообмена с окружающей средой, то есть система не получает тепла и не отдает его,  Изменение энтропии определяется как , следовательно, при адиабатном процессе энтропия остается постоянной. При адиабатном сжатии над газом совершают работу внешние силы, внутренняя энергия увеличивается: , температура газа увеличивается. Адиабатное сжатие происходит на этапе 4 – 1.

 ЗАДАНИЕ N 16 сообщить об ошибке Тема: Распределения Максвелла и Больцмана На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где  – доля молекул, скорости которых заключены в интервале скоростей от  до  в расчете на единицу этого интервала. Если, не меняя температуры взять другой газ с меньшей молярной массой и таким же числом молекул, то …

			максимум кривой сместится вправо в сторону больших скоростей
			площадь под кривой не изменится
			высота максимума увеличится
			площадь под кривой уменьшится