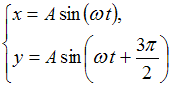10
.docx
![]() ЗАДАНИЕ
N 1 сообщить
об ошибке
Тема:
Энергия волны. Перенос энергии волной
В
упругой среде плотностью
ЗАДАНИЕ
N 1 сообщить
об ошибке
Тема:
Энергия волны. Перенос энергии волной
В
упругой среде плотностью ![]() распространяется
плоская синусоидальная волна. Если
амплитуда волны увеличится в 4 раза, а
частота в 2 раза, то плотность потока
энергии (вектор Умова) увеличится в
______ раз(-а).
распространяется
плоская синусоидальная волна. Если
амплитуда волны увеличится в 4 раза, а
частота в 2 раза, то плотность потока
энергии (вектор Умова) увеличится в
______ раз(-а).
|
|
|
64
| |
Решение:
Плотность
потока энергии, то есть количество
энергии, переносимой волной за единицу
времени через единицу площади площадки,
расположенной перпендикулярно направлению
переноса энергии, равна: ![]() где
где ![]() –
объемная плотность энергии,
–
объемная плотность энергии, ![]() –
скорость переноса энергии волной (для
синусоидальной волны эта скорость равна
фазовой скорости). Среднее значение
объемной плотности энергии равно:
–
скорость переноса энергии волной (для
синусоидальной волны эта скорость равна
фазовой скорости). Среднее значение
объемной плотности энергии равно: ![]() где
где ![]() –
амплитуда волны,
–
амплитуда волны, ![]() –
частота. Следовательно, плотность потока
энергии увеличится в 64 раза.
–
частота. Следовательно, плотность потока
энергии увеличится в 64 раза.
![]() ЗАДАНИЕ
N 2 сообщить
об ошибке
Тема:
Волны. Уравнение волны
Уравнение
бегущей волны имеет вид:
ЗАДАНИЕ
N 2 сообщить
об ошибке
Тема:
Волны. Уравнение волны
Уравнение
бегущей волны имеет вид: ![]() ,
где
,
где ![]() выражено
в миллиметрах,
выражено
в миллиметрах, ![]() –
в секундах,
–
в секундах, ![]() –
в метрах. Отношение амплитудного значения
скорости частиц среды к скорости
распространения волны равно …
–
в метрах. Отношение амплитудного значения
скорости частиц среды к скорости
распространения волны равно …
|
|
|
|
0,028 |
|
|
|
|
28 |
|
|
|
|
0,036 |
|
|
|
|
36 |
Решение:
Уравнение
плоской гармонической волны,
распространяющейся вдоль оси ОХ, имеет
вид: ![]() .
Здесь
.
Здесь ![]() –
амплитуда волны, (
–
амплитуда волны, (![]() )
– ее фаза,
)
– ее фаза, ![]() начальная
фаза,
начальная
фаза, ![]() –
циклическая частота,
–
циклическая частота, ![]() –
волновое число. Из сопоставления с
уравнением, приведенным в условии,
следует:
–
волновое число. Из сопоставления с
уравнением, приведенным в условии,
следует: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
Для волнового числа справедливо
соотношение
.
Для волнового числа справедливо
соотношение ![]() ,
где
,
где ![]() –
длина волны,
–
длина волны,![]() –
скорость ее распространения. Отсюда
скорость распространения волны равна
–
скорость ее распространения. Отсюда
скорость распространения волны равна  .
Скорость колебаний частиц среды
.
Скорость колебаний частиц среды ![]() ,
откуда амплитуда скорости равна
,
откуда амплитуда скорости равна ![]() .
Тогда искомое отношение равно
.
Тогда искомое отношение равно ![]() .
.
![]() ЗАДАНИЕ
N 3 сообщить
об ошибке
Тема:
Свободные и вынужденные колебания
В
колебательном контуре, состоящем из
катушки индуктивности
ЗАДАНИЕ
N 3 сообщить
об ошибке
Тема:
Свободные и вынужденные колебания
В
колебательном контуре, состоящем из
катушки индуктивности ![]() конденсатора
конденсатора ![]() и
сопротивления
и
сопротивления ![]() время
релаксации в секундах равно …
время
релаксации в секундах равно …
|
|
|
4
| |
Решение:
Коэффициент
затухания равен ![]() .
Время релаксации
.
Время релаксации ![]() –
это время, в течение которого амплитуда
колебаний уменьшается в
–
это время, в течение которого амплитуда
колебаний уменьшается в ![]() (~
2,7) раз.
(~
2,7) раз. 
![]() ЗАДАНИЕ
N 4 сообщить
об ошибке
Тема:
Сложение гармонических колебаний
Складываются
два взаимно перпендикулярных колебания.
Установите соответствие между номером
соответствующей траектории и законами
колебаний точки
ЗАДАНИЕ
N 4 сообщить
об ошибке
Тема:
Сложение гармонических колебаний
Складываются
два взаимно перпендикулярных колебания.
Установите соответствие между номером
соответствующей траектории и законами
колебаний точки ![]() вдоль
осей координат
вдоль
осей координат ![]()
![]()


|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
N 5 сообщить
об ошибке
Тема:
Дуализм свойств микрочастиц. Соотношение
неопределенностей Гейзенберга
Отношение
длин волн де Бройля для молекул водорода
и кислорода, соответствующих их наиболее
вероятным скоростям при одной и той же
температуре, равно …
ЗАДАНИЕ
N 5 сообщить
об ошибке
Тема:
Дуализм свойств микрочастиц. Соотношение
неопределенностей Гейзенберга
Отношение
длин волн де Бройля для молекул водорода
и кислорода, соответствующих их наиболее
вероятным скоростям при одной и той же
температуре, равно …
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
Решение:
Длина
волны де Бройля определяется
формулой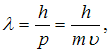 где
где ![]() –
постоянная Планка,
–
постоянная Планка, ![]() и
и ![]() –
масса и скорость частицы. Наиболее
вероятная скорость молекулы
–
масса и скорость частицы. Наиболее
вероятная скорость молекулы 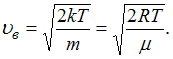 Здесь k –
постоянная Больцмана, R –
универсальная газовая постоянная,
Здесь k –
постоянная Больцмана, R –
универсальная газовая постоянная, ![]() –
молярная масса газа. Тогда
–
молярная масса газа. Тогда 
![]() ЗАДАНИЕ
N 6 сообщить
об ошибке
Тема:
Спектр атома водорода. Правило
отбора
Главное
квантовое число n определяет …
ЗАДАНИЕ
N 6 сообщить
об ошибке
Тема:
Спектр атома водорода. Правило
отбора
Главное
квантовое число n определяет …
|
|
|
|
энергию стационарного состояния электрона в атоме |
|
|
|
|
орбитальный механический момент электрона в атоме |
|
|
|
|
собственный механический момент электрона в атоме |
|
|
|
|
проекцию орбитального момента импульса электрона на заданное направление |
Решение:
Собственные
функции электрона в атоме водорода ![]() содержат
три целочисленных параметра: n, l и m.
Параметр n называется
главным квантовым числом, параметры l и m –
орбитальным (азимутальным) и магнитным
квантовыми числами соответственно.
Главное квантовое число nопределяет
энергию стационарного состояния
электрона в атоме.
содержат
три целочисленных параметра: n, l и m.
Параметр n называется
главным квантовым числом, параметры l и m –
орбитальным (азимутальным) и магнитным
квантовыми числами соответственно.
Главное квантовое число nопределяет
энергию стационарного состояния
электрона в атоме.
![]() ЗАДАНИЕ
N 7 сообщить
об ошибке
Тема:
Уравнения Шредингера (общие
свойства)
Стационарное
уравнение Шредингера в общем случае
имеет вид
ЗАДАНИЕ
N 7 сообщить
об ошибке
Тема:
Уравнения Шредингера (общие
свойства)
Стационарное
уравнение Шредингера в общем случае
имеет вид  .
Здесь
.
Здесь ![]() потенциальная
энергия микрочастицы. Электрону в
одномерном потенциальном ящике с
бесконечно высокими стенками соответствует
уравнение …
потенциальная
энергия микрочастицы. Электрону в
одномерном потенциальном ящике с
бесконечно высокими стенками соответствует
уравнение …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
N 8 сообщить
об ошибке
Тема:
Уравнение Шредингера (конкретные
ситуации)
На
рисунках схематически представлены
графики распределения плотности
вероятности обнаружения электрона по
ширине одномерного потенциального
ящика с бесконечно высокими стенками
для состояний с различными значениями
главного квантового числа n.
ЗАДАНИЕ
N 8 сообщить
об ошибке
Тема:
Уравнение Шредингера (конкретные
ситуации)
На
рисунках схематически представлены
графики распределения плотности
вероятности обнаружения электрона по
ширине одномерного потенциального
ящика с бесконечно высокими стенками
для состояний с различными значениями
главного квантового числа n.
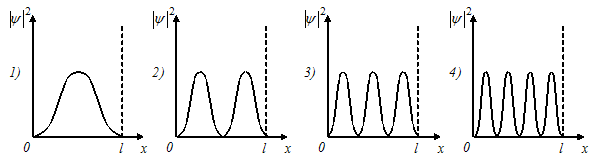 В
состоянии с n =
4 вероятность обнаружить электрон в
интервале от
В
состоянии с n =
4 вероятность обнаружить электрон в
интервале от ![]() до
до ![]() равна …
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ЗАДАНИЕ
N 9 сообщить
об ошибке
Тема:
Уравнения Максвелла
Физический
смысл уравнения Максвелла
ЗАДАНИЕ
N 9 сообщить
об ошибке
Тема:
Уравнения Максвелла
Физический
смысл уравнения Максвелла 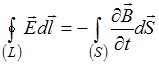 заключается
в следующем …
заключается
в следующем …
|
|
|
|
изменяющееся со временем магнитное поле порождает вихревое электрическое поле |
|
|
|
|
источником вихревого магнитного поля помимо токов проводимости является изменяющееся со временем электрическое поле |
|
|
|
|
«магнитных зарядов» не существует: силовые линии магнитного поля замкнуты |
|
|
|
|
источником электрического поля являются свободные электрические заряды |
![]() ЗАДАНИЕ
N 10 сообщить
об ошибке
Тема:
Явление электромагнитной индукции
На
рисунке представлена зависимость ЭДС
индукции в контуре от времени. Магнитный
поток сквозь площадку, ограниченную
контуром, увеличивается со временем по
закону
ЗАДАНИЕ
N 10 сообщить
об ошибке
Тема:
Явление электромагнитной индукции
На
рисунке представлена зависимость ЭДС
индукции в контуре от времени. Магнитный
поток сквозь площадку, ограниченную
контуром, увеличивается со временем по
закону ![]() (а,
b, c –
постоянные) в интервале …
(а,
b, c –
постоянные) в интервале …

|
|
|
|
В |
|
|
|
|
С |
|
|
|
|
А |
|
|
|
|
D |
|
|
|
|
Е |
![]() ЗАДАНИЕ
N 11 сообщить
об ошибке
Тема:
Магнитостатика
На
рисунке изображен вектор скорости
движущегося электрона:
ЗАДАНИЕ
N 11 сообщить
об ошибке
Тема:
Магнитостатика
На
рисунке изображен вектор скорости
движущегося электрона:
 Вектор
магнитной индукции
Вектор
магнитной индукции ![]() поля,
создаваемого электроном при движении,
в точке С направлен …
поля,
создаваемого электроном при движении,
в точке С направлен …
|
|
|
|
от нас |
|
|
|
|
сверху вниз |
|
|
|
|
на нас |
|
|
|
|
снизу вверх |
Решение:
Индукция
магнитного поля свободно движущегося
заряда равна  ,
где
,
где ![]() заряд
частицы,
заряд
частицы, ![]() скорость
частицы,
скорость
частицы, ![]() радиус-вектор
точки С. Используя определение векторного
произведения, находим, что вектор
радиус-вектор
точки С. Используя определение векторного
произведения, находим, что вектор ![]() направлен
«на нас», но, учитывая отрицательный
знак заряда частицы, получим окончательный
ответ – вектор
направлен
«на нас», но, учитывая отрицательный
знак заряда частицы, получим окончательный
ответ – вектор ![]() направлен
«от нас».
направлен
«от нас».
![]() ЗАДАНИЕ
N 12 сообщить
об ошибке
Тема:
Электрические и магнитные свойства
вещества
На
рисунке показана зависимость
поляризованности Р в
сегнетоэлектрике от напряженности Е внешнего
электрического поля:
ЗАДАНИЕ
N 12 сообщить
об ошибке
Тема:
Электрические и магнитные свойства
вещества
На
рисунке показана зависимость
поляризованности Р в
сегнетоэлектрике от напряженности Е внешнего
электрического поля:
 Участок
Участок ![]() соответствует …
соответствует …
|
|
|
|
остаточной поляризации сегнетоэлектрика |
|
|
|
|
спонтанной поляризации сегнетоэлектрика |
|
|
|
|
коэрцитивной силе сегнетоэлектрика |
|
|
|
|
поляризации насыщения сегнетоэлектрика |
![]() ЗАДАНИЕ
N 13 сообщить
об ошибке
Тема:
Электростатическое поле в вакууме
Заряд
1 нКл переместился
из точки, находящейся на расстоянии
1 см от
поверхности заряженного проводящего
шара радиусом 9 см,
в бесконечность. Поверхностная плотность
заряда шара 1,1·10-4 Кл/м2.
Работа сил поля (в мДж),
совершаемая при этом перемещении,
равна ______ .
(Ответ округлите до
целых.)
ЗАДАНИЕ
N 13 сообщить
об ошибке
Тема:
Электростатическое поле в вакууме
Заряд
1 нКл переместился
из точки, находящейся на расстоянии
1 см от
поверхности заряженного проводящего
шара радиусом 9 см,
в бесконечность. Поверхностная плотность
заряда шара 1,1·10-4 Кл/м2.
Работа сил поля (в мДж),
совершаемая при этом перемещении,
равна ______ .
(Ответ округлите до
целых.)
|
|
|
1
| |
Решение:
Работа
сил поля по перемещению заряда определяется
по формуле ![]() ,
где q – перемещаемый заряд,
,
где q – перемещаемый заряд, ![]() и
и ![]() –
потенциалы начальной и конечной точек
соответственно. В случае заряженного
шара потенциал на бесконечности
–
потенциалы начальной и конечной точек
соответственно. В случае заряженного
шара потенциал на бесконечности ![]() .
.  .
Тогда
.
Тогда 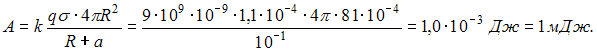
![]() ЗАДАНИЕ
N 14 сообщить
об ошибке
Тема:
Законы постоянного тока
Напряжение
на концах медного провода диаметром d и
длиной l равно
ЗАДАНИЕ
N 14 сообщить
об ошибке
Тема:
Законы постоянного тока
Напряжение
на концах медного провода диаметром d и
длиной l равно ![]() .
Если взять медный провод диаметром d,
но длиной 2l и
увеличить напряжение в 4 раза, то среднее
время дрейфа электронов от одного конца
проводника до другого …
.
Если взять медный провод диаметром d,
но длиной 2l и
увеличить напряжение в 4 раза, то среднее
время дрейфа электронов от одного конца
проводника до другого …
|
|
|
|
не изменится |
|
|
|
|
увеличится в 4 раза |
|
|
|
|
увеличится в 2 раза |
|
|
|
|
уменьшится в 4 раза |
Решение:
Время,
которое требуется в среднем для того,
чтобы электроны продрейфовали на
расстояние l,
определяется соотношением  ,
где
,
где ![]() –
средняя скорость упорядоченного движения
(дрейфа) электронов. Формула, связывающая
силу тока со средней скоростью
упорядоченного движения носителей
тока, имеет вид
–
средняя скорость упорядоченного движения
(дрейфа) электронов. Формула, связывающая
силу тока со средней скоростью
упорядоченного движения носителей
тока, имеет вид ![]() ,
где q0 –
заряд носителей, в данном случае –
электронов, n –
их концентрация, S –
площадь поперечного сечения проводника.
С учетом закона Ома для участка цепи
,
где q0 –
заряд носителей, в данном случае –
электронов, n –
их концентрация, S –
площадь поперечного сечения проводника.
С учетом закона Ома для участка цепи ![]() и
формулы для сопротивления
проводника
и
формулы для сопротивления
проводника ![]() получаем
выражение для средней скорости
направленного движения электронов
получаем
выражение для средней скорости
направленного движения электронов 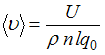 ,
из которого следует, что
,
из которого следует, что ![]() не
зависит от диаметра провода. Тогда время
дрейфа
не
зависит от диаметра провода. Тогда время
дрейфа  .
Таким образом, если взять медный провод
диаметром d,
но длиной 2l и
увеличить напряжение в 4 раза, то среднее
время дрейфа электронов от одного конца
проводника до другого не изменится.
.
Таким образом, если взять медный провод
диаметром d,
но длиной 2l и
увеличить напряжение в 4 раза, то среднее
время дрейфа электронов от одного конца
проводника до другого не изменится.
![]() ЗАДАНИЕ
N 15 сообщить
об ошибке
Тема:
Элементы специальной теории
относительности
Релятивистское
сокращение длины ракеты составляет
20%. При этом скорость ракеты равна …
ЗАДАНИЕ
N 15 сообщить
об ошибке
Тема:
Элементы специальной теории
относительности
Релятивистское
сокращение длины ракеты составляет
20%. При этом скорость ракеты равна …
|
|
|
|
0,6 с |
|
|
|
|
0,8 с |
|
|
|
|
0,2 с |
|
|
|
|
0,4 с |
![]() ЗАДАНИЕ
N 16 сообщить
об ошибке
Тема:
Кинематика поступательного и вращательного
движения
Диск
катится равномерно по горизонтальной
поверхности со скоростью
ЗАДАНИЕ
N 16 сообщить
об ошибке
Тема:
Кинематика поступательного и вращательного
движения
Диск
катится равномерно по горизонтальной
поверхности со скоростью ![]() без
проскальзывания. Вектор скорости точки
А, лежащей на ободе диска, ориентирован
в направлении …
без
проскальзывания. Вектор скорости точки
А, лежащей на ободе диска, ориентирован
в направлении …

|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
3 |
|
|
|
|
4 |
Решение:
Качение
однородного кругового цилиндра (диска)
по плоскости является плоским движением.
Плоское движение можно представить как
совокупность двух движений: поступательного,
происходящего со скоростью ![]() центра
масс, и вращательного вокруг оси,
проходящей через этот центр. Тогда
центра
масс, и вращательного вокруг оси,
проходящей через этот центр. Тогда ![]() .
Поскольку диск катится без проскальзывания,
скорость точки диска, соприкасающейся
с поверхностью, равна нулю. Отсюда
следует, что
.
Поскольку диск катится без проскальзывания,
скорость точки диска, соприкасающейся
с поверхностью, равна нулю. Отсюда
следует, что ![]() .
Вектор
.
Вектор ![]() направлен
по касательной к окружности в
рассматриваемой точке (для точки А – в
направлении 3). Тогда вектор скорости
направлен
по касательной к окружности в
рассматриваемой точке (для точки А – в
направлении 3). Тогда вектор скорости ![]() точки
А ориентирован в направлении 2.
точки
А ориентирован в направлении 2.