Стандартная энергия Гиббса образования.

Под стандартной энергией Гиббса образования ΔG^о_обр понимают изменение энергии Гиббса при реакции образования 1 моль сложного вещества, находящегося в стандартном состоянии из простых веществ. Это определение подразумевает, что стандартная энергия Гиббса образования простого вещества, устойчивого в стандартных условиях, равна нулю.

Изменение энергии Гиббса, как и изменение энтальпии и энтропии системы, не зависит от пути процесса. Поэтому для реакции вида

а А + b В + ... → с С + d D + …

изменение стандартной энергии Гиббса ΔG^о равно разности между суммой стандартных энергий Гиббса образования продуктов реакции и суммой стандартных энергий Гиббса образования исходных веществ:

ΔG^о=[c ∆G^о_(C) + d ∆G^о_(D) + …] – [a ∆G^о_(A) + b ∆G^о_(B) + …],

или

ΔG^о = Σ∆G^о_{обр, прод.} – Σ∆G^о_{обр, исх.}

Есть случаи, когда реакция термодинамически разрешена, а самопроизвольно не идёт. Например:

2H_2(г) + O_{2 (г)} = 2H₂O_(ж), ΔG = – 474,38 кДж

В обычных условиях эта реакция практически не идёт. Но стоит внести в смесь подходящий катализатор (мелкодисперсную платину) или просто поднести горящую спичку, реакция произойдёт со взрывом: это гремучий газ.

Если реакция термодинамически не разрешена, условия подобрать невозможно.

6. Константа равновесия и изобарно–изотермический потенциал реакции

Константа химического равновесия зависит от природы реагентов и температуры. Она связана с изменением стандартной энергии Гиббса химической реакции ΔG^о уравнением

ΔG^о = –RT ln K, ΔG^о₂₉₈ (кДж) = –5,71 lg K₂₉₈ (7)

Приведённое уравнение позволяет по величине ΔG^о вычислить К, а затем и равновесные концентрации (парциальные давления) реагентов. Большим отрицательным значениям ΔG^о (ΔG<<0) отвечают большие значения К (К>>1), т.е. в равновесной смеси преобладают продукты взаимодействия. При больших положительных значениях ΔG^о (ΔG^о>>0) в равновесной смеси преобладают исходные вещества (К<<1). Если учесть, что ΔG = ΔН – TΔS = –RT lnK, то после некоторого преобразования получим

(8)

Из этого уравнения видно, что константа равновесия очень чувствительна к изменению температуры. Для эндотермических процессов повышение температуры отвечает увеличению константы равновесия, для экзотермических – её уменьшению. От давления (если оно не очень велико) константа равновесия не зависит.

Зависимость константы равновесия от энтальпийного и энтропийного факторов свидетельствует о влиянии на нее природы реагентов.

В литературе применяются термины–синонимы: свободная энергия, свободная энергия при постоянном давлении, потенциал Гиббса, функция Гиббса, энергия Гиббса, изобарный потенциал, изобарно–изотермический потенциал.

7. Термохимические измерения и вычисления

Измерение тепловых эффектов называется калориметрией. Методика и оборудование, применяемые в калориметрии, зависят от характера изучаемого процесса. Реакции горения обычно изучают при помощи так называемой калориметрической бомбы. Реакции в калориметрической бомбе протекают при постоянном объеме.

Большинство реакций осуществляется при постоянном давлении. Измерение изменения энтальпии этих реакций осуществляется в калориметрах различных конструкций, которые представляют собой по возможности лучше изолированный от теплообмена с внешней средой сосуд с мешалкой и термометром.

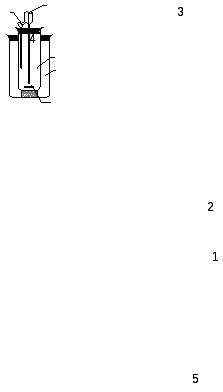
Упрощенный калориметр (рис.3) состоит из двух стаканов: наружного (1) и внутреннего, реакционного (2).

Реакционный стакан с магнитной мешалкой (5) закрывается крышкой с отверстиями: для термометра (3); для воронки (4).

Рис. 3. Устройство калориметра

Количество теплоты, выделяющейся или поглощающейся в калориметре, определяется по формуле

, (9)

где t_к – конечная температура;

t_н– начальная температура;

с_i – удельные теплоемкости калориметрического сосуда, калориметрической жидкости и исследуемого вещества;

m_i – массы реакционного сосуда, жидкости и исследуемого вещества.

При использовании стеклянного реакционного сосуда теплоемкостью калориметрического сосуда можно пренебречь из-за его малой теплопроводности. Удельную теплоемкость растворов можно принять равной теплоемкости для воды: 4,2 кДж/кг град или 1 ккал/кг·град.

Тогда уравнение (10) примет следующий вид для стеклянного сосуда:

Q = (t_к – t_н)∙4,2·m (кДж) или

(10)

Q = (t_к – t_н)∙1·m (ккал),

где m –масса воды растворенного вещества.

(Масса воды или растворов находится как произведение объема жидкocти на ее плотность, т.е. m=ρ·V. Плотность воды ρ равна 1 г/мл, плотность разбавленных растворов считать равной также 1 г/мл).

Пересчет теплового эффекта на 1 моль вещества, т.е. нахождение величины ∆H, производится по формуле

, (11)

где n – число молей вещества.

Все работы по определению изменения энтальпии химических процессов необходимо проводить в следующей последовательности.

1. Поместить в реакционный сосуд измеренный мензуркой объем воды или раствора и дождаться выравнивания температуры калориметра и окружающей среды. Для этого, выждав 3–5 мин, записывать показания термометра в течение трех минут с интервалом в 1 мин. Если температура практически не меняется, принять ее за величину t_н.

2. Быстро внести через сухую воронку взвешенное на весах или измеренное цилиндром количество реагирующего вещества и, непрерывно перемешивая раствор мешалкой, производить замеры температуры через 0,5–

1 мин.

Результаты наблюдений записывать в виде таблицы:

Время от начала опыта, мин	0	0,5	1,0	1,5	2,0	2,5	3,0	3,5	4,0	5,0	6,0
Температура, °С

3. Построить график изменения температуры во времени на миллиметровой бумаге, отложив на оси ординат температуру, а на оси абсцисс – время в минутах. На рис.4 приведен примерный вид этого графика.

4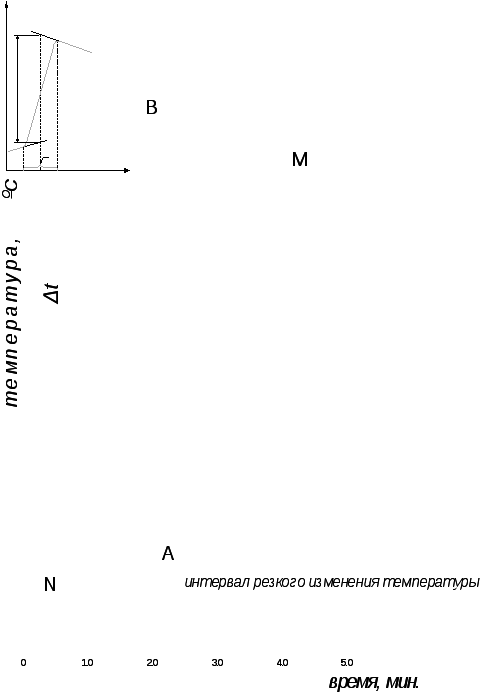. С помощью полученного графика найти изменение температуры в ходе опыта, ∆t = t_к – t_н. Для этого произвести экстраполяцию плавного линейного хода температуры конечного и исходного периодов времени (если температура в начале опыта не менялась, то прямая этого участка зависимости будет параллельна оси абсцисс).

Отрезок времени, за который наблюдалось резкое изменение температуры, разделить пополам, из полученной точки восстановить перпендикуляр до пересечения с экстраполированными прямыми BM и NA.

Величина отрезка перпендикуляра АВ, отсекаемого этими прямыми, соответствует изменению температуры

∆t = t_к – t_н.

Рис. 4. Зависимость температуры

от времени

Используя описанные выше рекомендации, произведите измерение изменения температуры и вычислите значение энтальпии для некоторых процессов.