
II класс 3 вид
Пример. На
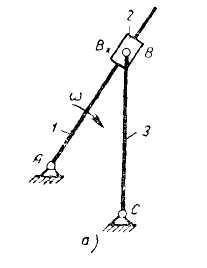
(рис. а)
изображена схема четырехзвенного
механизма с тремя вращательными и одной
поступательной парой. Ведущее звено 1
связано с ползуном 2 в поступательную
пару; звено 3 связано с ползуном во
вращательную пару В.
Угловая скорость звена 1 направлена по
часовой стрелке, величина ее известна.
Определить
![]() .
.
Отметим на звене 1 точку ВХ, расположенную под точкой В, т. е. находящуюся на расстоянии АВХ от точки А, равном АВ.
Для определения
![]() можем написать два векторных уравнения:
можем написать два векторных уравнения:
![]()
![]()
В соответствии
с первым уравнением мы должны
провести
![]() -
вектор
-
вектор![]() -и к концу этого вектора пристроить
вектор
-и к концу этого вектора пристроить
вектор![]()
скорости
![]()
Длина вектора
![]() =
=![]() где
где![]() — длина АВХ,
— длина АВХ,
![]() —угловая скорость
звена 1 и
—угловая скорость
звена 1 и
![]() — масштаб плана скоростей. Длина
вектора bХb
не может быть пока определена, так как
величина скорости
— масштаб плана скоростей. Длина
вектора bХb
не может быть пока определена, так как
величина скорости
![]() неизвестна. Так как точка BХ
относительно точки В может перемешаться
только вдоль звена 1, то проведя вектор
неизвестна. Так как точка BХ
относительно точки В может перемешаться
только вдоль звена 1, то проведя вектор
![]() перпендикулярно звену 1, от точки bХ
проводим линию действия
перпендикулярно звену 1, от точки bХ
проводим линию действия
![]() параллельно
звену 1 (рис.б).
параллельно
звену 1 (рис.б).
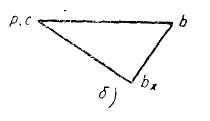
В соответствии со вторым уравнением точку с помещаем в полюсе, так как Vc = О, и от точки с проводим линию действия Vbc перпендикулярно к ВС, так как точка В относительно точки С может перемещаться только по окружности с радиусом ВС.
Точкой b
пересечения линий действия определяется
величина и направление
![]() —
вектор
—
вектор![]() .
.
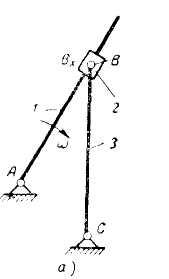 Пример
. Построить
план ускорений для механизма, схема
которого приведена на (рис. а).
Пример
. Построить
план ускорений для механизма, схема
которого приведена на (рис. а).
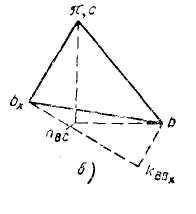
План ускорений II класс 3 вид
При составлении
векторных уравнений для определении
ускорений
![]() необходимо принять во внимание, что
точка В, перемещаясь по вращающемуся
звену, движется с поворотным (кориолисовым)
ускорением, которое будем обозначать
также буквой а с верхним индексом k.
необходимо принять во внимание, что
точка В, перемещаясь по вращающемуся
звену, движется с поворотным (кориолисовым)
ускорением, которое будем обозначать
также буквой а с верхним индексом k.
Для определения
![]() можно написать два векторных уравнения:
можно написать два векторных уравнения:
![]()
![]()
Определяем величины и направления геометрических слагаемых в правых частях обоих уравнений:
|
Ускорение |
Величина |
Направление |
|
|
где
|
От точки ВХ (рис. а) к точке А, так как при вращении звена 1 с равномерной скоростью полное ускорение равно нормальному |
|
|
|
- |
|
|
|
Определяется
вектором скорости
|
|
|
Неизвестна |
По звену 1 |
|
|
Равна нулю, так как точка С неподвижна |
- |
|
|
где
cd – длина вектора
|
От точки В к точке С |
|
|
Неизвестна |
Перпендикулярна звену 3 |
Разделив величины
ускорений на масштаб
![]() плана ускорений, определим длины
векторов. Приняв во внимание указанные
выше направления всех векторов в
соответствии с первым из приведенных
выше уравнений, проводим последовательно
(рис.б)
вектор
плана ускорений, определим длины
векторов. Приняв во внимание указанные
выше направления всех векторов в
соответствии с первым из приведенных
выше уравнений, проводим последовательно
(рис.б)
вектор
![]() ускорения
ускорения![]() ,
вектор
,
вектор![]() ускорения
ускорения![]() и линию действия ускорения
и линию действия ускорения![]() .
В соответствии со вторым уравнением
от точкис,
совпадающей с полюсом
.
В соответствии со вторым уравнением
от точкис,
совпадающей с полюсом
![]() ,
проводим вектор
,
проводим вектор![]() ускорения
ускорения![]() и из конца этого вектора линию действия
ускорения
и из конца этого вектора линию действия
ускорения![]() .
Точкойb
пересечения линий действия ускорений
.
Точкойb
пересечения линий действия ускорений
![]() и
и![]() определяется конец вектора
определяется конец вектора![]() ускорения
ускорения![]() .
.


