
- •Дифференциальное исчисление
- •1. Базовые понятия Слова мы пишем буквами, а числа – цифрами (рис. 1.1).
- •2. Изображение чисел
- •3. Понятие функции
- •Или просто
- •4. Изображение функции
- •5. Прямо пропорциональная зависимость
- •8. Обратная функция
- •9. Функция, заданная параметрическими уравнениями
- •14. Бесконечно малые и бесконечно большие переменные
- •15. Основные правила обращения с пределами
- •16. Раскрытие неопределённостей
- •17. Эквивалентные переменные
- •18. Первая замечательная эквивалентность
- •19. Экспонента и натуральный логарифм
- •20. Вторая замечательная эквивалентность
- •21. Сводка формул для раскрытия неопределённостей
- •22. Непрерывная функция
- •23. Свойства непрерывных функций
- •24. Метод половинного деления
- •26. Понятие производной
- •31. Механический смысл производной
- •32. Дифференциал
- •33. Геометрический смысл производной
- •37. Дифференциалы высших порядков
- •38. Механический смысл второй производной
- •39. Правило лопиталя
- •40. Возрастание и убывание функции. Максимум и минимум
- •43. Асимптоты
- •45. Понятие функции двух переменных
- •46. Изображение функции двух переменных
- •47. Частные производные и дифференциал функции
- •51. Экстремум функции двух переменных
- •Содержание
- •1. Базовые понятия……………………………………………………………………………1
23. Свойства непрерывных функций
♦ 1. При сложении, вычитании, умножении, делении непрерывных функций получается непрерывная функция.
(При делении нужно,
естественно, следить, чтобы знаменатель
![]() ).
).
♦ 2. Сложная функция, состоящая из непрерывных функций, тоже непрерывна.
Из этих свойств и утверждения (22.1) вытекает, что
каждая элементарная функция непрерывна в своей области определения.
♦ 3. Если функция непрерывна и возрастает (убывает), то обратная к ней функция тоже непрерывна и возрастает (убывает).
♦ 4. Всякая непрерывная в замкнутом интервале функция
а) имеет наименьшее и наибольшее значения,
б) принимает все промежуточные значения.
24. Метод половинного деления
Пусть точка
![]() располагается ниже
оси
располагается ниже
оси
![]() а точка
а точка
![]() выше оси
выше оси
![]() (рис. 24.1). Когда вы
будете соединять
(рис. 24.1). Когда вы
будете соединять
![]() с
с
![]() какой-нибудь линией, вы обязательно
пересе - чёте ось
какой-нибудь линией, вы обязательно
пересе - чёте ось
![]() Поэтому если известно уравнение этой
линии, можно найти его ко - рень
Поэтому если известно уравнение этой
линии, можно найти его ко - рень
![]() точку пересечения с осью
точку пересечения с осью
![]()
Пусть линия
![]() есть график функции
есть график функции
![]() на участке
на участке
![]() (рис. 24.1) .
(рис. 24.1) .
Как найти, хотя бы
приближённо, координату
![]() точки пересечения?
точки пересечения?
В ы
находите среднюю точку
ы
находите среднюю точку
![]() по формуле
по формуле
![]() .
Искомая точка
.
Искомая точка
![]() оказыва ется между
оказыва ется между
![]() и
и
![]() поэтому вы находите следующую среднюю
точку
поэтому вы находите следующую среднюю
точку
![]() по формуле
по формуле
![]() Точка
Точка
![]() будет ближе к
будет ближе к
![]() ,
чем точка
,
чем точка
![]() ..
Искомая точка
..
Искомая точка
![]() оказывается Рис. 24.1
оказывается Рис. 24.1
между
![]() и
и
![]() поэтому вы находите следующую среднюю
точку
поэтому вы находите следующую среднюю
точку
![]() по формуле
по формуле
![]() И так далее.
И так далее.
Так как
![]() то число
то число
![]() есть корень уравнения
есть корень уравнения
![]()
З
а д а ч а 1.
Найдите корень уравнения
![]() применив метод половинного деления.
применив метод половинного деления.
□ 1)
Поверим, лежит ли корень в интервале
![]()
Для
этого обозначим через
![]() левую
часть уравнения:
левую
часть уравнения:
![]()
Тогда
на концах интервала будем иметь
![]()
![]() Получились числа с разными знаками; это
значит, что корень уравнения
Получились числа с разными знаками; это
значит, что корень уравнения
![]() находится в данном интервале.
находится в данном интервале.
2)
Возьмём среднюю точку
![]() Тогда
Тогда
![]() отрицательное
число.
отрицательное
число.
Так
как
![]() то
корень находится между точками 4 и 8.
то
корень находится между точками 4 и 8.
3)
Возьмём среднюю точку
![]() Тогда
Тогда
![]() положительное
число. Так как
положительное
число. Так как
![]() то корень находится между точками 4 и
6.
то корень находится между точками 4 и
6.
4)
Возьмём среднюю точку
![]() Тогда
Тогда
![]()
Следовательно,
значение
![]() есть корень нашего уравнения. ■
есть корень нашего уравнения. ■
25. ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Гиперболическим синусом, косинусом, тангенсом, котангенсом называются следующие функции
![]() (25.1)
(25.1)
![]() (25.2)
(25.2)
![]()
![]()
Графики этих функций показаны на рис. 25.1 – 25.4.

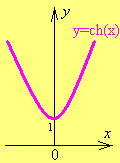
Рис. 25.1 Рис. 25.2


Рис. 25.3 Рис. 25.4
С помощью определений (25.1), (25.2) нетрудно доказать равенства
![]()
![]()
![]()
26. Понятие производной
Пусть имеется
непрерывная функция
![]()
Над ней вы можете выполнить следующие действия:
► построить её график (рис. 26.1);
► на оси
![]() точкой изобразить величину
точкой изобразить величину
![]() и дать её бесконечно малое прира -щение
и дать её бесконечно малое прира -щение
![]() (т. е. от точки
(т. е. от точки
![]() отложить бесконечно малый отрезок
отложить бесконечно малый отрезок
![]() ).
).
Тогда величина
![]() получит приращение
получит приращение
![]() .
.
► вычислить дробь
(отношение)
![]() которая
может оказаться новой функцией,
которая
может оказаться новой функцией,
о бозначаемой
бозначаемой
![]() или
или
![]() или
или
![]() .
.
|
Производной от
функции
называется новая
функция
определяемая по формуле
|
Отыскание производной от функции называется
дифференцированием функции.
Дифференцировать = искать производную. Рис. 26.1
Дадим ещё одно определение:
|
Если функция
|
|
то
функция
|
Если же производная не существует или бесконечна, то функцию называют недифференцируемой.
Производную от функции
![]() обозначают также
обозначают также
![]()
![]()
![]()
27. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ
Покажем, что
|
Если функция дифференцируема,
|
|
то эта функция непрерывна.
|
♥ Дано:
![]() дифференцируемая функция.
дифференцируемая функция.
Это значит, что
величина
![]() есть конечная функция.
есть конечная функция.
Это равенство перепишем
так:
![]() .
.
Но
![]() мало, поэтому и
мало, поэтому и
![]() будет мало.
будет мало.
Выполнение соотношений
![]() и
и
![]()
означает, что функция
![]() непрерывна. ■
непрерывна. ■
Обратное утверждение
не всегда верно: если функция
![]() непрерывна, то функция
непрерывна, то функция
![]() может и не быть дифференцируемой.
может и не быть дифференцируемой.
28. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Функции, с которыми будем иметь дело, будем считать дифференцируемыми.
1. Докажем, что
![]() производная
константы равна нулю.
производная
константы равна нулю.
♥ Возьмём функцию
![]() Нужно доказать, что
Нужно доказать, что
![]()
![]()
![]()
![]()
![]() ■
■
Пример:
![]()
2. Докажем, что
![]()
♥ Возьмём функцию
![]() Нужно доказать, что
Нужно доказать, что
![]()
![]()
![]()
![]()
![]() ■
■
3. Докажем, что
![]() производная
суммы равна сумме производных.
производная
суммы равна сумме производных.
♥ Возьмём функцию
![]()
Тогда
![]()
![]()
![]()
![]()
![]() ■
■
Пример:
![]()
4. Докажем, что
![]() формула
производной произведения.
формула
производной произведения.
♥ Возьмём функцию
![]()
Тогда
![]()
![]()
![]()
отсюда
![]()
![]()
![]()
![]()
![]()
![]() ■
■
Пример:
![]()
С л е д с т в и е 1.
![]() постоянный
множитель можно переносить за знак
производной:
постоянный
множитель можно переносить за знак
производной:
![]()
Пример:
![]()
С л е д с т в и е 2.
![]() формула
производной разности:
формула
производной разности:
![]()
5. Докажем, что
![]() формула
производной дроби.
формула
производной дроби.
♥ Возьмём функцию
![]() (а)
(а)
Тогда
![]()
![]()
![]()
![]()
![]()
![]() ■
■
Пример:
![]()
6. Докажем, что
![]() формула производной
сложной функции.
формула производной
сложной функции.
♥ Дано
![]()
Тогда
![]() или
или
![]() ■
■
Пример:
![]()
![]()
![]()
7. Докажем, что если
имеется неявная
функция
![]() ,
то
,
то
![]()
Эта формула позволяет
находить
![]() .
.
♥ Дано
![]()
Это значит, что при
любом
![]()
![]()
поэтому
![]() ■
■
Соберём в таблицу основные правила дифференцирования.
|
1.
|
2.
|
|
3.
|
4.
|
|
5.
|
6.
|
|
7. Если дана неявная
функция
то
|
|
29. ПРОИЗВОДНЫЕ ПРОСТЕЙШИХ ФУНКЦИЙ
Докажем справедливость следующих формул.
1. Производная степенной функции определяется по формуле
![]() (29.1)
(29.1)
♥ Дано
![]()
Тогда
![]()
![]()
![]()
![]()
![]()
![]()
отсюда
![]()
![]()
![]() ■
■
З
а д а ч а 1.
Найти
![]()
□
![]() ■
■
З
а д а ч а 2.
Найти
![]()
□
![]()
![]() ■
■
2. Производная показательной функции определяется по формуле
![]() (29.2)
(29.2)
♥ Дано
![]()
Тогда
![]()
![]()
![]()
отсюда
![]()
![]() ■
■
З
а д а ч а 3.
Найти
![]()
□
![]()
![]() ■
■
Следствие.
![]()
![]() отсюда
отсюда
![]()
![]()
![]()
![]()
З
а д а ч а 4.
Найти
![]()
□
![]() ■
■
3. Производная логарифмической функции определяется по формуле
![]() (29.3)
(29.3)
♥ Дано
![]()
Тогда
![]() (а)
(а)
![]()
![]()
(а)![]()
![]() ■
■
З
а д а ч а 5.
Найти
![]()
□
![]()
![]()
![]() ■
■
С л е д с т в и е.
![]()
![]()
![]()
![]() ■
■
4. Производные тригонометрических функций определяются по формулам
![]()
![]()
![]()
![]()
♥ Дано
![]()
Тогда
![]()
![]()
![]()
отсюда
![]()
![]()
![]() получилась первая формула.
получилась первая формула.
Для второй формулы
получаем
![]() отсюда
отсюда
![]()
![]()
![]()
Для третьей формулы
получаем
![]()
![]()
![]()
![]()
Для четвёртой формулы получаем аналогично
![]()
![]()
![]() ■
■
5. Производные обратных тригонометрических функций определяются по формулам
![]()
![]()
![]()
![]()
♥
![]() Дано
Дано
![]()
Тогда
![]() (а)
(а)
![]() (б)
(б)
![]()
![]()
но
![]() (а)
(а)
![]() (б)
(б)
![]()
поэтому
![]()
![]()
Для второй формулы
получаем
![]()
![]()
![]()
Докажем третью
формулу. Дано
![]()
Тогда
![]() (в)
(в)
![]()
![]()
![]()
но
![]() (в)
(в)
![]() поэтому
поэтому
![]()
Для вывода четвёртой
формулы воспользуемся равенством
![]()
тогда
![]()
![]() ■
■
6. Производные гиперболических функций определяются по формулам
![]()
![]()
![]()
![]()
♥
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ■
■
30. ТАБЛИЦА ФОРМУЛ ДИФФЕРЕНЦИРОВАНИЯ
Здесь приводится
список формул, в котором
![]() произвольная
дифференцируе -мая функция,
произвольная
дифференцируе -мая функция,
![]() независимая
переменная,
независимая
переменная,
![]() константа.
константа.
|
1.
|
2.
|
|
3.
|
4.
|
|
5.
|
6.
|
|
7.
|
8.
|
|
9.
|
10.
|
|
11.
|
12.
|
|
13.
|
14.
|
|
15.
|
16.
|
|
17.
|
18.
|
По этим формулам вы можете находить производную функции любой сложности.
З
а д а ч а 1.
Найти производную функции
![]()
□
![]()
![]()
![]() ■
■
Итак, для нахождения производной приходится применять правила дифференци - рования и таблицу формул дифференцирования. Поэтому можно дать такое оп -ределение производной:
Производной от функции называется новая функция, полученная применени - ем таблицы формул дифференцирования и правил дифференцирования.
