16. Раскрытие неопределённостей

Пусть вам нужно найти предел

Если ищется предел в котором

, или , или , или , или , или , или

то называется неопределённостью соответствующего вида, а вычисление предела называется раскрытием неопределённости.

Посмотрите, как раскрываются некоторые неопределённости.

З а д а ч а 1. Найти

ٱ ■

З а д а ч а 2. Найти

□ ■

З а д а ч а 3. Найти

□ ■

З а д а ч а 4. Найти

□

■

З а д а ч а 5. Найти

□

■

Полезной может оказаться следующая формула

Здесь в числителе и знаменателе оставляются члены с наибольшими степенями.

♥ Докажем эту формулу.

■

З а д а ч а 6. Найти

□ ■

17. Эквивалентные переменные

Эквивалентные переменные часто бывают полезными при раскрытии неопреде - лённости.

Если

то говорят, что переменная эквивалентна переменной при

и пишут при .

Здесь символ ~ есть знак эквивалентности.

Докажем утверждение.

Если

то

(18.1)

(17.1)

♥ Дано (а)

Тогда

Выполнение равенства означает, что ■

Так как , то, согласно (17.1), получаем эквивалентность

(17.2)

( В следующем пункте будет доказана более точная эквивалентность).

Примем без доказательства, что

Если

то

(17.3)

18. Первая замечательная эквивалентность

Первой замечательной эквивалентностью называется следующее выражение

(18.1)

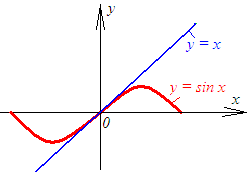♥ Посмотрите на рис. 18.1. Вблизи точки графики функций и сливаются, поэтому можно написать при Эти соотношения равносильны выражению (18.1). ■

Формула (18.1) означает, что

Рис. 18.1

Эту формулу называют первым замечательным пределом.

З а д а ч а 1. Найдите

□ ■

Из основной формулы (18.1) получаются следующие полезные формулы

♥ Согласно (18.1) отсюда

- получилась первая формула.

Далее, (18.1), (17.2) - вторая формула.

Из сразу вытекает - третья формула.

Наконец,

- четвёртая формула. ■