
- •Дифференциальное исчисление
- •1. Базовые понятия Слова мы пишем буквами, а числа – цифрами (рис. 1.1).
- •2. Изображение чисел
- •3. Понятие функции
- •Или просто
- •4. Изображение функции
- •5. Прямо пропорциональная зависимость
- •8. Обратная функция
- •9. Функция, заданная параметрическими уравнениями
- •14. Бесконечно малые и бесконечно большие переменные
- •15. Основные правила обращения с пределами
- •16. Раскрытие неопределённостей
- •17. Эквивалентные переменные
- •18. Первая замечательная эквивалентность
- •19. Экспонента и натуральный логарифм
- •20. Вторая замечательная эквивалентность
- •21. Сводка формул для раскрытия неопределённостей
- •22. Непрерывная функция
- •23. Свойства непрерывных функций
- •24. Метод половинного деления
- •26. Понятие производной
- •31. Механический смысл производной
- •32. Дифференциал
- •33. Геометрический смысл производной
- •37. Дифференциалы высших порядков
- •38. Механический смысл второй производной
- •39. Правило лопиталя
- •40. Возрастание и убывание функции. Максимум и минимум
- •43. Асимптоты
- •45. Понятие функции двух переменных
- •46. Изображение функции двух переменных
- •47. Частные производные и дифференциал функции
- •51. Экстремум функции двух переменных
- •Содержание
- •1. Базовые понятия……………………………………………………………………………1
43. Асимптоты
Асимптота – это прямая, к которой приближается график при неограничен - ном удалении от начала координат (рис. 43.1).


Рис. 43.1 Рис. 43.2
График функции
![]() может иметь как
вертикальные, так и невертикальные
может иметь как
вертикальные, так и невертикальные
асимптоты (рис. 43.2).
Прямая
![]() является
вертикальной асимптотой, если хотя бы
один из двух пре – делов
является
вертикальной асимптотой, если хотя бы
один из двух пре – делов
![]() равен
равен
![]() Обычно
вертикальная
асимптота имеется в точках оси
Обычно
вертикальная
асимптота имеется в точках оси
![]() не входящих в ОДЗ, и на границе ОДЗ.
не входящих в ОДЗ, и на границе ОДЗ.
Вертикальных асимптот
может быть сколь угодно. Количество
невертикальных асимптот может быть
только не больше
2: одна при
![]() вторая при
вторая при
![]()
О том, как ищется невертикальная асимптота, говорится в следующем утверждении:
|
Если имеется
функция
|
|
то прямая
|
З
а д а ч а 1. Найдите асимптоты графика
функции
![]()
□ а)
Сначала найдём вертикальные асимптоты.
Наша функция не существует, когда
знаменатель
![]() Проверим, является ли вертикаль
Проверим, является ли вертикаль
![]() асимптотой, для чего найдём предел:
асимптотой, для чего найдём предел:
![]()
![]()
![]()
Следовательно,
прямая
![]() - вертикальная асимптота.
- вертикальная асимптота.
б)
Ищем невертикальные асимптоты
![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Следовательно,
прямая
![]() - невертикальная асимптота. ■
- невертикальная асимптота. ■
44. ОБЩИЙ ПЛАН ИССЛЕДОВАНИЯ ФУНКЦИИ
И ПОСТРОЕНИЯ ЕЁ ГРАФИКА
План исследования функции и построения её графика заключается в выполнении следующих шагов:
1. Находим возможные вертикальные асимптоты и ОДЗА.
2. Определяем чётность, нечётность, периодичность.
3. Находим точки пересечения с осями координат.
4. Находим асимптоты вертикальные и невертикальные.
5. Находим производную, интервалы возрастания, убывания и точки экстремума.
6. Находим вторую производную, интервалы выпуклости, вогнутости и точки пере -гиба.
7. При необходимости находим дополнительные точки графика.
З
а д а ч а 1. Проведите полное исследование
функции
![]() и постройте её график.
и постройте её график.
□ 1.
Из «запрещённого» условия![]() получаем
получаем
![]() - уравнение возможной вертикальной
асимптоты. Нарисуем её на плоскости
- уравнение возможной вертикальной
асимптоты. Нарисуем её на плоскости
![]() (рис. 44.1). Итак,
(рис. 44.1). Итак,
![]()
2. Функция не периодична, потому что не содержит тригонометрических функций.
Проверим
её чётность:
![]()
следовательно, относительно системы координат график не симметричен.
3 .
а) Ищем вертикальные асимптоты. Для
этого найдём односторонние пределы
функции в «запрещённой» точке
.
а) Ищем вертикальные асимптоты. Для
этого найдём односторонние пределы
функции в «запрещённой» точке
![]() .
.
Н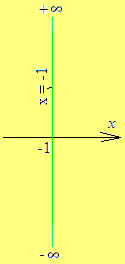 аходим
правый предел:
аходим
правый предел:
![]()
![]()
Значит,
прямая
![]() есть вертикальная асимптота: при
есть вертикальная асимптота: при
![]() происходит
происходит
![]() .
.
На
рис 44.2 этот процесс показан куском
![]() графика.
графика.
Находим
левый предел:
![]()
![]()
Таким
образом, при
![]() происходит
происходит
![]() .
.
На
рис 44.2 этот процесс показан куском
![]() графика.
графика.
б) Ищем
невертикальные асимптоты
![]() .
.
Рассмотрим
первый случай, когда
![]() :
:
![]()
![]()
Рис. 44.1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Вывод:
при
![]() невертикальной асимптоты не существует
(т. к.
невертикальной асимптоты не существует
(т. к.
![]() не число).
не число).
Рассмотрим
второй случай, когда
![]() :
:
![]()
![]() ,
,
![]()
![]() Следовательно,
Следовательно,
![]()
![]() .
.
Итак,
при
![]() имеем невертикальную асимптоту
имеем невертикальную асимптоту
![]() Это – ось
Это – ось
![]() (рис. 44.3).
(рис. 44.3).


Рис. 44.2 Рис. 44.3
4 .
При
.
При
![]() получаем
получаем
![]() ,
поэтому
,
поэтому
![]() - точка пересечения с осью
- точка пересечения с осью
![]() (рис. 44.4).
(рис. 44.4).
При
![]() получаем
получаем
![]() отсюда
отсюда
![]()
Это
уравнение не имеет решений, поэтому с
осью
![]() график не пересекается.
график не пересекается.
5. Находим производную
![]()
![]()
Приравниваем
числитель и знаменатель к нулю и получаем
значения
![]()
![]() Рисуем ось
Рисуем ось
![]() наносим
на неё точки
наносим
на неё точки![]()
![]() и определяем знак функции
и определяем знак функции
![]() в трёх интервалах (рис. 44.5). Этот знак
указывает, где функция растёт и где
убывает. Рис. 44.4
в трёх интервалах (рис. 44.5). Этот знак
указывает, где функция растёт и где
убывает. Рис. 44.4
При переходе через точку непрерывности
![]()
 функция
функция
![]() меняет
знак с – на +, поэтому
меняет
знак с – на +, поэтому
![]() есть точка минимума. Минимальное
значение функции равно
есть точка минимума. Минимальное
значение функции равно
![]()
В
точке![]() рисуем «ямку» (рис.
рисуем «ямку» (рис.
44.6). Рис. 44.5
6. Находим вторую производную
![]()


![]() Приравниваем
числитель и знаменатель к нулю и получаем
значение
Приравниваем
числитель и знаменатель к нулю и получаем
значение
![]() Рисуем
ось
Рисуем
ось
![]() ,
наносим точку
,
наносим точку
![]() и определяем знак
и определяем знак
функции
![]() в двух интервалах (рис. 44.7). Этот знак
показывает, где функция
в двух интервалах (рис. 44.7). Этот знак
показывает, где функция
![]() выпукла и где вогнута. График на рис.
44.6 согласуется с этими результатами.
выпукла и где вогнута. График на рис.
44.6 согласуется с этими результатами.
Исследование функции и построение её графика на этом завершается.

Рис. 44.6 Рис. 44.7

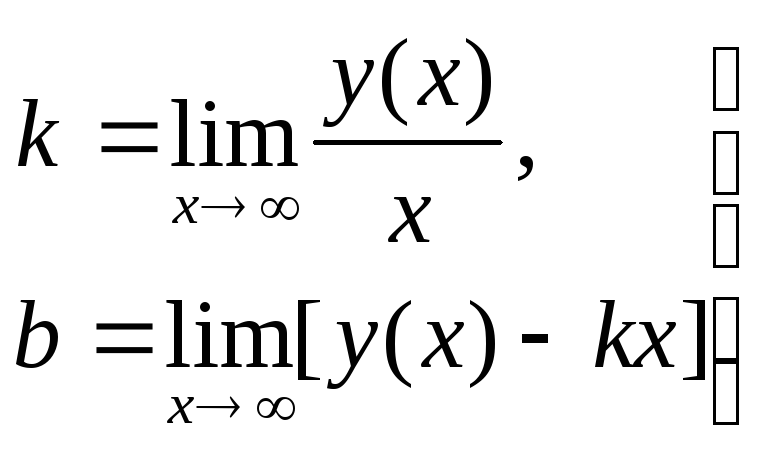 - числа,
- числа,