37. Дифференциалы высших порядков

Обычный дифференциал вычисляемый по формуле

(37.1)

называют дифференциалом первого порядка. Дифференциал от т. е. называют дифференциалом второго порядка и обозначают (читают «дэ два игрек»). Таким образом, Аналогично, дифференциал третьего порядка есть

Вообще, дифференциал го порядка определяется по формуле

Дифференциал второго и более высокого порядка называется дифференциалом высшего порядка. Найдём формулы вычисления этих дифференциалов.

Для дифференциала второго порядка получаем

Величину принято обозначать . Итак,

Аналогично, и т. д. Таким образом,

… ,

отсюда

. . . ,

Так обозначаются производные высших порядков.

38. Механический смысл второй производной

Пусть за бесконечно малое время скорость тела изменилась на Тогда ве -

личина даст скорость изменения скорости, т. е. ускорение, обозначаемое обычно буквой или Следовательно, или

Но поэтому Итак,

Вторая производная от пути по времени есть ускорение:

Это механический смысл второй производной.

З а д а ч а 1. Дана зависимость пути от времени: Найдите скорость и ускорение тела в момент времени

□ Находим скорость тела в момент времени

Находим ускорение тела в момент времени Отсюда при получаем . ■

39. Правило лопиталя

Это правило удобно при вычислении пределов.

Правило Лопиталя.

♥ Дана дробь

С л у ч а й 1. Пусть при происходит следующее:

Выражение (б) означает, что

или

,

,

или, в других обозначениях,

Итак,

С л у ч а й 2. Пусть при происходит следующее:

или

Но поэтому или

Итак, здесь также ■

Неопределённости остальных типов всегда можно свести к этим двум типам или

З а д а ч а 1. Найти предел

■

■

40. Возрастание и убывание функции. Максимум и минимум

Докажем следующие утверждения.

	Функция растёт

Функция убывает

♥ Из рис 40.1 вытекает цепочка равносильных утверждений:

функция растёт,

касательная также идёт вверх,

угол острый,

.

Для убывающей функции доказательство аналогичное. ■

Рис. 40.1 Рис. 40.2

Посмотрите на рис. 40.2. В точке производная (так как касательная горизонтальная), а в точке производная не существует (так как касательной здесь нет).Точки и являются критическими, потому что

точки, в которых производная либо равна 0, либо не существует, называются

критическими. Рис. 40.2 показывает справедливость следующих предложений:

Если 1) критическая точка, 2) при переходе через производная меняет знак с на ,

то точка минимума.

Если 1) критическая точка, 2) при переходе через производная меняет знак с на ,

то точка максимума.

З а д а ч а 1. Найдите точки экстремума функции и её экстремальные значения.

□ Находим производную:

Приравняем её к нулю и найдём корни: критические точки.

Нарисуем ось нанесём критические точки (рис. 40.3), определим знаки производной в трёх интервалах, поведение функции на них и определим точки максимума и минимума.

Рис. 40.3

Видим, что точка максимума, точка минимума.

Максимальное значение равно

минимальное значение равно

■

Наличие точек экстремума можно определить (правда, не всегда) и при помощи второй производной.

Если и
то точка максимума	то точка минимума.

♥ Посмотрите на рис. 40.2. При переходе через критическую точку функция меняет знак с на , т. е. уменьшается. А раз функция уменьшается, то её производная отрицательна, следовательно, ■

З а д а ч а 2. Найдите точки экстремума функции с помощью второй производной.

□ 1) Находим первую производную затем из уравнения находим критические точки

2) Находим вторую производную и вычисляем её значения в критических точках: значит точка максимума; поэтому точка минимума. ■

41. НАИМЕНЬШЕЕ И НАИБОЛЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ

Дана функция непрерывная на (рис. 41.1).

Требуется найти её наименьшее и наибольшее значения.

Для этого нужно:

1) найти критические точки внутри ;

2) вычислить значения функции в критических точках и в точках

3) из них выбрать наименьшее значение и наибольшее значение.

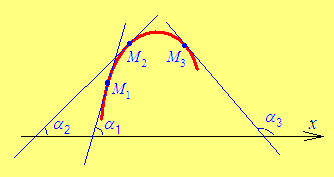
Рис. 41.1 Рис. 42.1

З а д а ч а 1. Найдите наименьшее и наибольшее значения функции в интервале

□ 1) Находим производную

Составляем уравнение и находим критические точки

Точка не попала в интервал поэтому её выбрасываем.

2) Вычисляем значения

3) Получаем ответ: ■

42. ВЫПУКЛОСТЬ, ВОГНУТОСТЬ, ТОЧКИ ПЕРЕГИБА

На рис. 42.1 показана выпуклая кривая. При движении слева направо касатель - ная поворачивается по часовой стрелке, т. е. в отрицательном направлении. Зна - чит, величина (тангенс угла наклона касательной к оси ) уменьшается. Поэтому можно дать следующие определения:

Если при движении слева направо величина уменьшается,

то кривая называется выпуклой.

Если при движении слева направо величина увеличивается,

то кривая называется вогнутой.

В самом деле, на рис. 42.1 видно, что здесь потому что тупой угол.

Точка, отделяющая выпуклую часть от вогнутой, называется точкой перегиба (рис. 42.2). Наличие выпуклости или вогнутости можно определить по второй производной:

кривая выпуклая

кривая вогнутая

♥ Имеем следующую цепочку утверждений:

,

функция убывает, Рис. 42.2

величина уменьшается,

кривая выпуклая.

Второй случай, когда , доказывается аналогично. ■

Из этих утверждений следует, что

Если 1) в точке функция либо равна 0, либо не существует; 2) функция меняет знак при переходе через точку ,

то - точка перегиба.

З а д а ч а 1. Найдите точки перегиба графика функции

□ Находим

Видим, что функция существует при любом .

Составляем уравнение и получаем

Определяем знак в окрестности этой точки и поведение функции (рис. 42.3):

Видим, что есть точка перегиба. ■ Рис. 42.3