46. Метод хорд

Другой метод, который обладает большей скоростью сходимости, чем методы деления отрезка пополам и Фибоначчи, называется методом хорд. Основная идея, заложенная в его основе, заключается в том, что функция на отрезке , содержащим корень, заменяется прямой линией, которая проходит через две точки на плоскости с координатами, определяемыми величинамии, и соответствующими значениями функции при этих значениях. Точка пересечения прямой с осью абсциссобъявляется приближенным значением корня. Она делит исходный интервал на два отрезка, один из которых содержит искомый корень. Процедура определения отрезка, содержащего корень такова же, что и для методов деления отрезка пополам и Фибоначчи. Приведем расчетные формулы для вычисления координаты точки, которая получается в методе хорд. Для этого получим уравнение прямой, проходящей через две точки с координатамии. При этоми. Поскольку уравнение прямой имеет вид

,

(2.1.27)

то для нахождения неизвестных ииспользуем соотношения

,

(2.1.28)

.

(2.1.29)

Далее решая систему линейных уравнений (2.1.28) – (2.1.29), получаем для и

,

(2.1.30)

.

(2.1.31)

Подставляя их значения в (2.1.27), находим уравнение для прямой, которая проходит через две заданные точки на плоскости XOY: ,

.

(2.1.32)

Так как точка является точкой пересечения прямой (2.1.32) с осью абсцисс, то она находится из условия

или.

(2.1.33)

Отсюда находим

.

(2.1.34)

Таким образом, для вычисления необходимо знать значения функции на концах интервала. Пошаговая схема алгоритма имеет вид:

1. ввод начальных данных: точности вычислений , началаи конца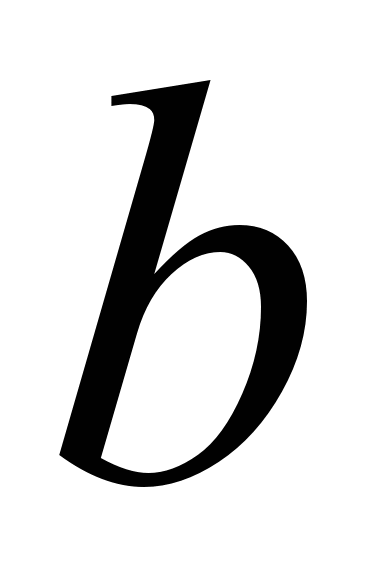для интервала, содержащего корень;

2. вычисляем значение функции в точках и:и;

3. определяем значение по формуле (2.1.34) и вычисляем значение функции в этой точке;

4. если , тои, иначеи;

5. вычисляем по формуле (2.1.34) и значение функции в данной точке;

6. если выполнено неравенство , тои идем кшагу 4, иначе к следующемушагу;

7. выводим значения корня и функции.

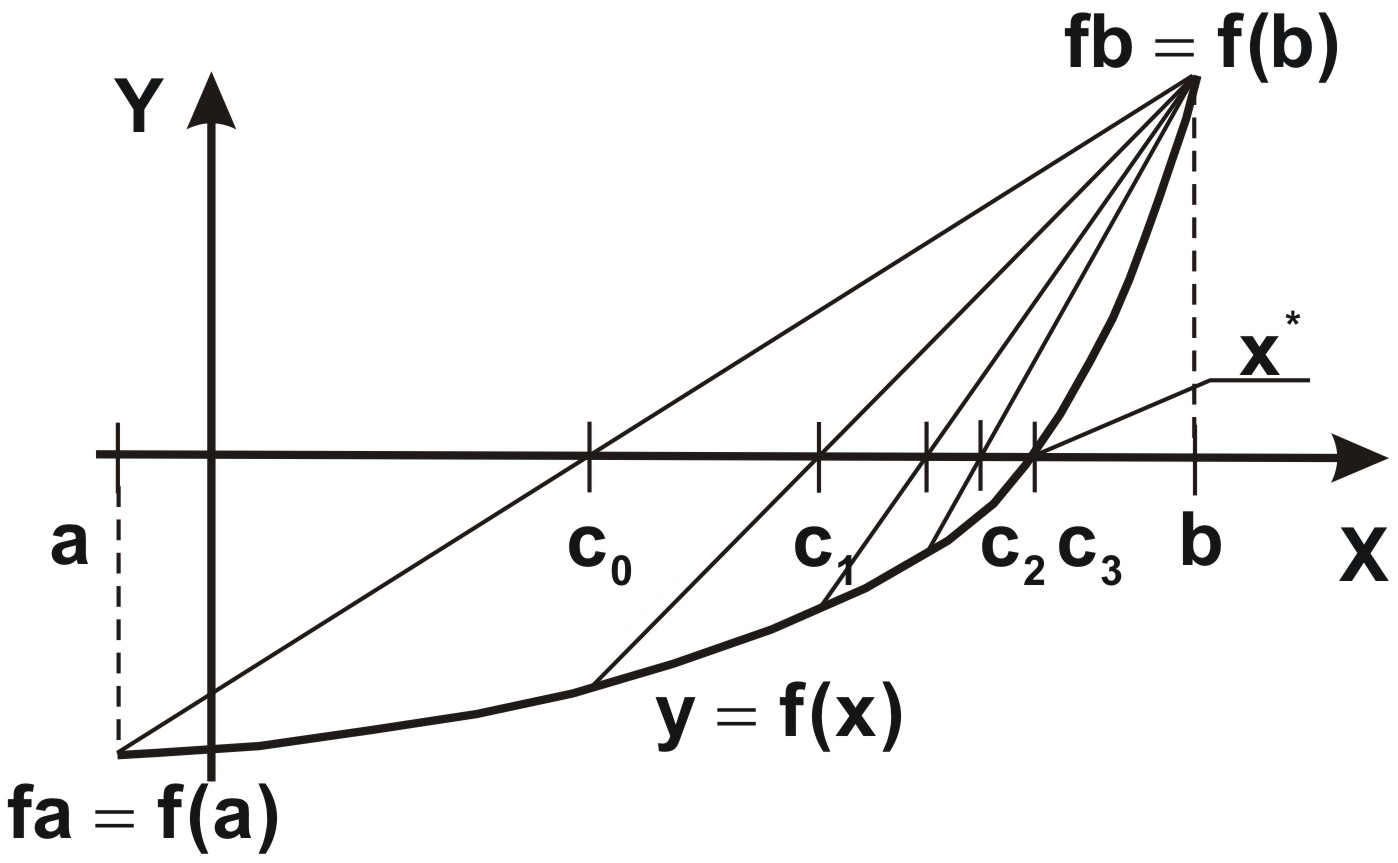Рис. 2.1.4. Графическая интерпретация работы метода хордГрафическая интерпретация метода хорд (иное название метод секущих) представлена на рис. 2.1.4. Работу метода хорд исследуем на примере вычисления корня функции (2.1.24). Результаты расчетов представлены в таблице 4 с точностью.Таблица 4Пример, показывающий работу метода хорд

№ итерации
1	0.4	2	1.482924	-0.378837	0.187405	-0.510182
2	1.482924	2	1.864107	-0.510182	0.187405	-0.050477
3	1.864107	2	1.893689	-0.050477	0.187405	-0.002954
4	1.893689	2	1.895393	-0.002954	0.187405	-0.000166

Применение метода хорд позволило найти корень функции (2.1.24), который равен 1.895393, а значение самой функции в найденной точке принимает значение, равное -0.000166. Данный результат получен за четыре итерации, что значительно меньше, чем при использовании метода золотого сечения. Это говорит о том, что метод хорд обладает более высокой скоростью сходимости по сравнению с методами бисекций и золотого сечения.