

(Сейчас начнется!!!)
Обыкновенные дифференциальные уравнения
Явная схема (Эйлера)
1) Решение уравнения
y ' f (x, y) на отрезке[a, b] с заданным начальным условием.
2) Решения уравнения
y ' f (x, y) с условием на значение интеграла от
искомой функции отрезке
. [a, b]
Неявная схема
Решение уравнения
y '' y cos(x) на отрезке[0, ] с
заданными граничными условиями.
2
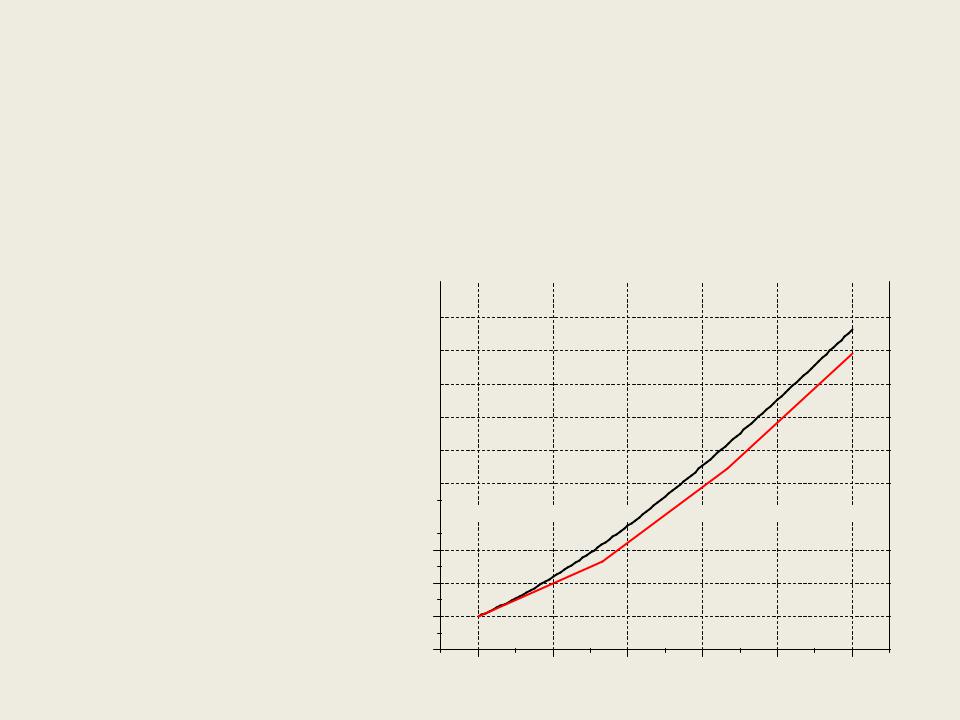
Явная схема
Решение уравнения y ' |
y x |
на отрезке[0,1] |
||||||||||||||||||||||||||||
y x |
||||||||||||||||||||||||||||||
|
%создаем сетку: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a=0; b=1; |
n=101; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h=(b-a)/(n-1); |
|
Решения для n=101 и n=4: |
||||||||||||||||||||||||||||
|
x=a:h:b; |
|
||||||||||||||||||||||||||||
|
%задаем начальные и граничные |
3,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
условия: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y0=1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
xt=a; |
|
2,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
yt=y0; |
|
2,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
%задаем функцию: |
2,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
f='(yt+xt)/(yt-xt)'; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
y=zeros(1,n); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
y(1)=y0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
%ищем решение уравнения: 1,6 
























































































|
for k=2:n, |
1,4 |
|
|
|
|
|
|
yt=yt+h*eval(f); |
1,2 |
|
|
|
|
|
|
y(k)=yt; |
|
|
|
|
|
|
1,0 |
|
|
|
|
|
||
|
xt=x(k); |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
end, |
0,8 |
|
|
|
|
|
|
%строим график решения: |
0,0 |
0,2 |
0,4 |
0,6 |
0,8 |
1,0 |
|
|
|
|
|
3 |
||
|
plot(x,y), grid |
|
|
|
|
|
|
|
|
|
|
|
|
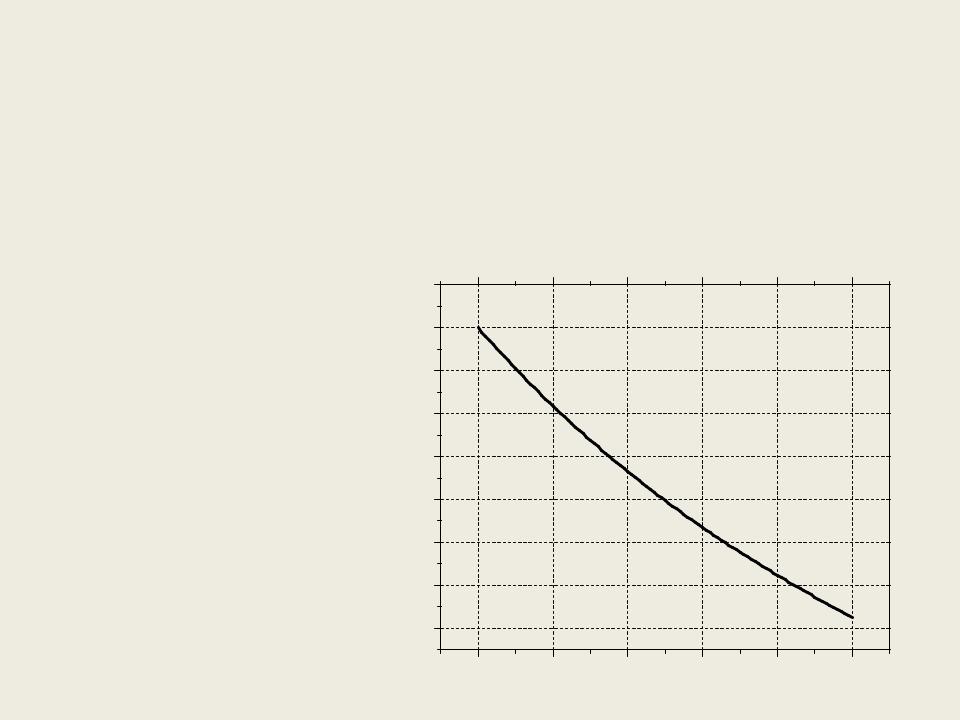
Явная схема |
|
|||
|
y ' |
6 x2 y2 |
[1,1.5] |
|
Решение уравнения |
x2 на отрезке |
|||
|
|
|||
%создаем сетку:
a=1; b=1.5; n=101;
h=(b-a)/(n-1);
x=a:h:b;
|
%задаем начальные и граничные |
2,1 |
|
|
|
|
|
|
|
условия: |
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
y0=2; |
2,0 |
|
|
|
|
|
|
|
xt=a; |
1,9 |
|
|
|
|
|
|
|
yt=y0; |
|
|
|
|
|
||
|
|
|
|
|
|
|||
|
%задаем функцию: |
1,8 |
|
|
|
|
|
|
f='(6-xt^2*yt^2)/(-xt^2)'; |
1,7 |
|
|
|
|
|
||
|
y=zeros(1,n); |
|
|
|
|
|
||
|
|
|
|
|
|
|||
|
y(1)=y0; |
1,6 |
|
|
|
|
|
|
|
%ищем решение уравнения: |
|
|
|
|
|
||
|
|
|
|
|
|
|||
|
for k=2:n, |
1,5 |
|
|
|
|
|
|
|
yt=yt+h*eval(f); |
1,4 |
|
|
|
|
|
|
|
y(k)=yt; |
|
|
|
|
|
||
|
|
|
|
|
|
|||
|
xt=x(k); |
1,3 |
|
|
|
|
|
|
|
end, |
1,0 |
1,1 |
1,2 |
1,3 |
1,4 |
1,5 |
|
|
%строим график решения: |
|||||||
|
|
|
|
|
4 |
|||
|
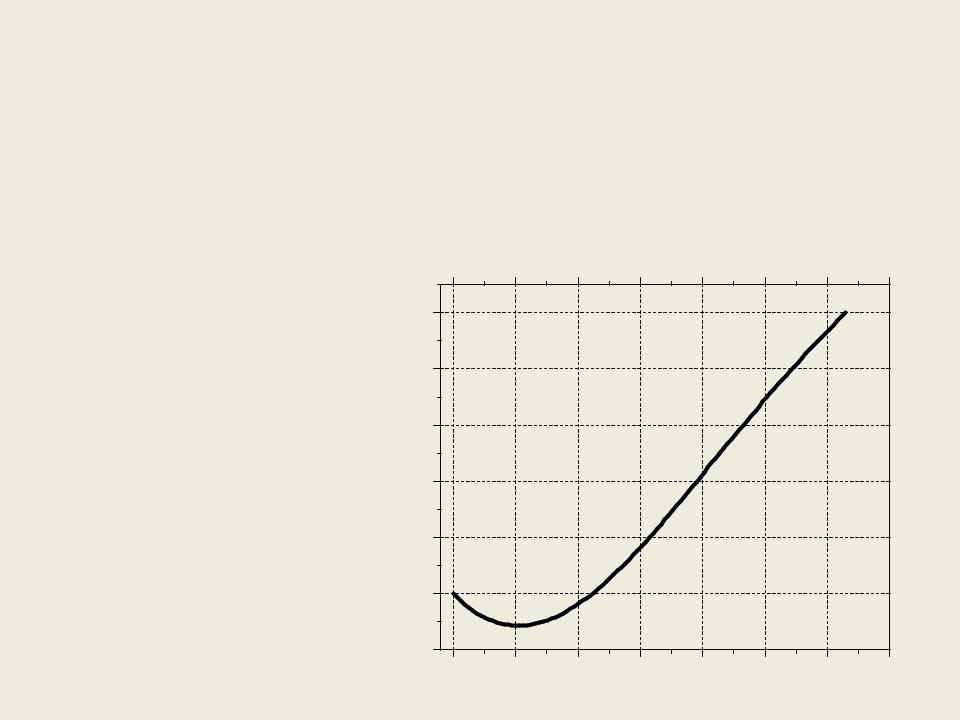
plot(x,y), grid |
|
|
|
|
|
||
|
|
|
|
|
|
|||
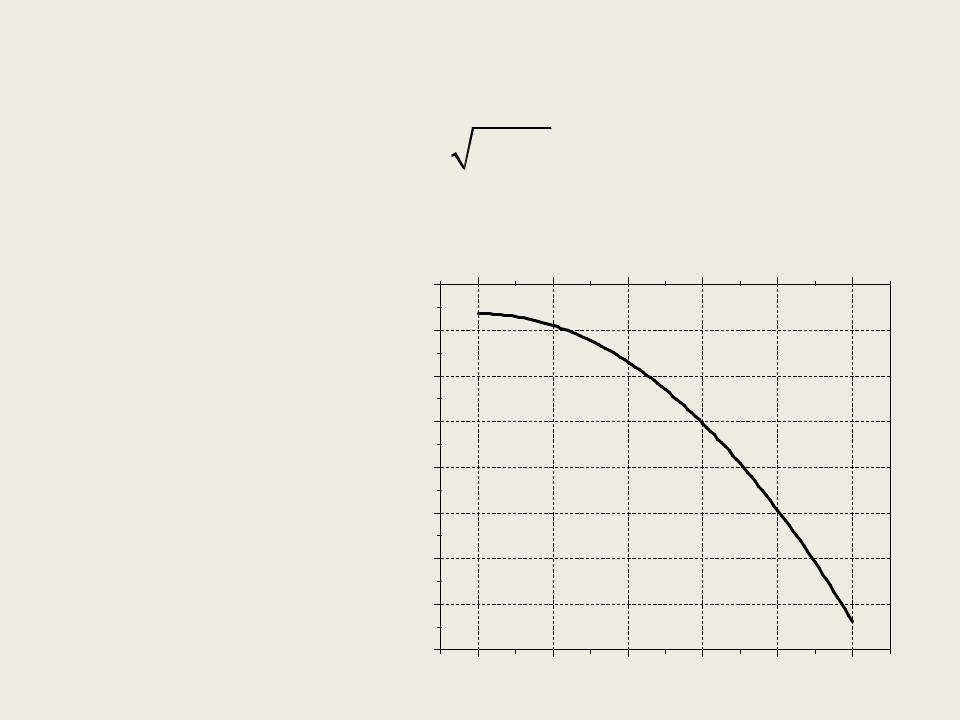
Явная схема
Решение уравнения y ' |
xy |
на отрезке [0, 0.5] |
||
|
||||
1 x2 |
||||
|
%создаем сетку: |
|
||
|
a=0; b=.5; n=101; |
|
|
|
h=(b-a)/(n-1);
x=a:h:b;
|
%задаем начальные и граничные |
2,75 |
|
|
|
|
|
|
условия: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y0=exp(1); |
2,70 |
|
|
|
|
|
|
xt=a; |
|
|
|
|
|
|
|
yt=y0; |
2,65 |
|
|
|
|
|
|
|
|
|
|
|
||
|
%задаем функцию: |
2,60 |
|
|
|
|
|
|
f=‘-xt*yt/(1-xt^2)^.5'; |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y=zeros(1,n); |
2,55 |
|
|
|
|
|
|
y(1)=y0; |
|
|
|
|
|
|
|
%ищем решение уравнения: |
2,50 |
|
|
|
|
|
|
for k=2:n, |
2,45 |
|
|
|
|
|
|
yt=yt+h*eval(f); |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y(k)=yt; |
2,40 |
|
|
|
|
|
|
xt=x(k); |
|
|
|
|
|
|
|
end, |
2,35 |
|
|
|
|
|
|
%строим график решения: |
0,0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
|
|
|
|
|
5 |
||
|
plot(x,y), grid |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Явная схема |
|
|
|
|
||
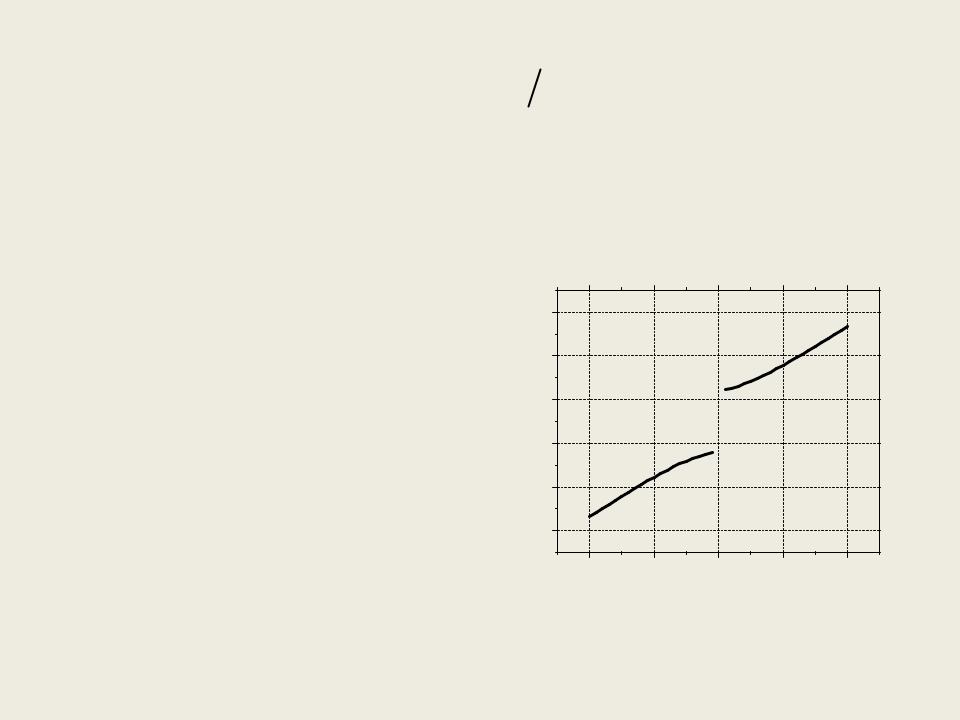
Решение уравнения y ' ( y x) |
( y x) |
с условием на |
||||||||
значение интеграла от y на[a, b] |
|
|
|
|
||||||
|
a=0; |
b=1; |
n=101; |
|
График зависимости значения |
|||||
|
h=(b-a)/(n-1); |
|
|
|||||||
|
|
интеграла от начальных |
|
|||||||
|
x=a:h:b; |
|
|
|
|
|||||
|
|
|
параметров: |
|
|
|
||||
|
y0=-2:.1:2; |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
xt=a; |
|
|
|
|
3 |
|
|
|
|
|
yt=y0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
f='(yt+xt)./(yt-xt)'; |
|
|
2 |
|
|
|
|
||
|
y=zeros(length(y0),n); |
%задает нулевой |
интеграла |
|
|
|
|
|
||
|
массив |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y(:,1)=y0; |
|
|
|
|
|
|
|
||
|
|
значение |
0 |
|
|
|
|
|||
|
%Заполняем массив решений: |
|
|
|
|
|||||
|
|
|
|
|
||||||
|
for k=2:n, |
|
|
-1 |
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
yt=yt+h*eval(f); |
|
|
|
|
|
|
|
||
|
y(:,k)=yt; |
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
xt=x(k); |
|
|
|
-2 |
-1 |
0 |
1 |
2 |
|
|
end, |
|
|
|
|
|
граничные условия (y(0)) |
|
||
|
|
|
|
|
|
|
|
|
||
|
%Строим график зависимости значения |
|
ans = |
|
|
|
|
|||
|
интеграла от начальных параметров: |
|
|
|
|
|
||||
|
|
-1.2673 |
|
-0.9985 |
|
|
||||
|
plot(y0,h*sum(y')),grid, |
|
|
|
|
|
||||
|
|
1.8018 |
|
2.4956 |
|
6 |
||||
|
ginput |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
Неявная схема
y '' y cos(x)
y(0) 0, y( ) 1 |
с граничными условиями |
Решение уравнения |
%Задаем сетку:
n=101;
h=pi/(n-1);
x=0:h:pi;
%Задаем функцию (столбцом):
f=[0,h^2*cos(x(2:n-1)),1]';
%задаем вспомогательную строку:
v=[-2-h^2,1,zeros(1,n-2)];
%строим матрицу Тёплица:
M=toeplitz(v);
M(1,1)=1;
M(1,2)=0;
M(n,n-1)=0;
M(n,n)=1;
%ищем решение
y=M\f;
%строим решение
plot(x,y),grid
1,0 |
|
|
|
|
|
|
|
0,8 |
|
|
|
|
|
|
|
0,6 |
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
0,0 |
|
|
|
|
|
|
|
-0,2 |
|
|
|
|
|
|
|
0,0 |
0,5 |
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
3,5 |
|
|
|
|
|
|
|
7 |

