Добавил:

okley Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

Численные методы

Файл:

Литература / Козин Р.Г. Алгоритмы численных методов линейной алгебры и их программная реализация

.pdf

Скачиваний:

Добавлен:

07.09.2025

Размер:

4.33 Mб

Скачать

☆

1 / 261 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Министерство науки и высшего образования Российской Федерации

Национальный исследовательский ядерный университет «МИФИ»

Р.Г. Козин

АЛГОРИТМЫ ЧИСЛЕННЫХ МЕТОДОВ ЛИНЕЙНОЙ АЛГЕБРЫ

И ИХ ПРОГРАММНАЯ РЕАЛИЗАЦИЯ

Учебно-методическое пособие

Издание 2-е, исправленное и дополненное

Москва 2019

УДК [512.64:004.4]:519.6(07)

ББК 22.143я7+22ю19я7+32ю973ю202-018я7 К59

Козин Р.Г. Алгоритмы численных методов линейной алгебры и их про-

граммная реализация: Учебно-методическое пособие. Изд. 2-е, испр. и доп. –

М.: НИЯУ МИФИ, 2019. – 252 с.

Учебно-методическое пособие знакомит с чиленными методами решения задач линейной алгебры. Рассматриваются алгоритмы этих методов и подробно обсуждаются особенности их программной реализации как на языках высокого уровня, так и в среде свободно распространяемого математического пакета Maxima. Каждый тематический раздел завершается вопросами для самоконтроля. В заключении приведены темы заданий для практикума и приложение с описанием некоторых встроенных команд математического пакета Maxima.

Пособие предназначено для студентов, обучающихся по специальности «Прикладная математика и информатика», а также для поддержки лекций, практических занятий и лабораторных работ по курсу «Специальные главы математики».

Книга может быть полезна инженерам и аспирантам при решении конкретных практических задач математической физики.

Рецензент канд. физ.-мат. наук, доц. Н.В. Овсянникова

ISBN 978-5-7262-2635-4	© Национальный исследовательский
	ядерный университет «МИФИ», 2012, 2019

	Оглавление
Введение...................................................................................................................		4
Глава 1. Нормы вектора и матриц,
мера обусловленности матрицы............................................................................		5
1.1.	Норма вектора............................................................................................	5
1.2.	Норма матрицы...........................................................................................	7
1.3. Мера обусловленности и ранг матрицы...................................................		15
Глава 2. Методы решения систем линейных уравнений...................................		31
2.1.	Итерационные методы решения систем
	линейных уравнений................................................................................	31
2.2. Прямые методы решения системы линейных уравнений........................		68
2.3. Метод регуляризации для решения
	плохо обусловленных систем.................................................................	131
2.4. Решение систем с прямоугольными матрицами....................................		135
Глава 3. Методы решения задачи на собственные значения..........................		146
3.1. Собственные значения и собственные вектора матрицы.......................		146
3.2. Решение частичной проблемы собственных чисел
	для симметричной матрицы...................................................................	149
3.3. Решение задачи на собственные значения
	методом Данилевского...........................................................................	157
3.4.	Модифицированный метод Данилевского.............................................	168
3.5.	Метод Крылова.......................................................................................	174
3.6. Определение собственных векторов в общем случае............................		181
3.7.	Метод вращения.....................................................................................	183
Глава 4. Алгоритмы для работы с полиномами...............................................		198
4.1. Подсчет значения полинома и деление на множители..........................		198
4.2.	Локализация корней полинома...............................................................	201
4.3. Метод парабол для нахождения всех корней полинома........................		116
Задания для практикума....................................................................................		229
Список литературы.............................................................................................		231
Приложение. Некоторые сведения о математическом пакете Maxima..........		232

ВВЕДЕНИЕ

Методы решения задач линейной алгебры являются основополагающими в прикладной математике, поскольку большинство реальных вычислительных задач из других разделов математики, как правило, сводятся к аппроксимирующим их задачам линейной алгебры. Кроме того, результаты линейной алгебры непосредственно используются при вычислении конкретных прикладных величин.

Наиболее востребованными задачами линейной алгебры являются следующие.

1. Найти вектор x с координатами xi , i 1 n , являющейся решение системы линейных уравнений

Ax b ,

где A ( Aij , i, j 1 n ) – исходная матрица; b (bi , i 1 n ) – заданный вектор правых частей системы.

2.Для заданной матрицы A вычислить определитель det(A) .

3.Найти матрицу A 1 , обратную заданной A, для которой выполняется матричное равенство A 1 A E , где E – единичная мат-

рица ( Eij ij ).

4. Для заданной матрицы A определить собственные числа i и соответствующие им собственные векторы xi , которые удовлетво-

ряют следующему матричному уравнению Ax x . 5. Нахождение корней полинома:

n
Pn (x) ai xn i a0 xn a1xn 1 ... an 0	,
i 0

выделение из полинома линейных и квадратичных множителей.

ГЛАВА 1. НОРМЫ ВЕКТОРА И МАТРИЦ, МЕРА ОБУСЛОВЛЕННОСТИ МАТРИЦЫ

Введем понятия норм вектора и матрицы, которые используются при «интегральной» оценке результатов операций, выполняемых над этими распределенными объектами.

1.1. Норма вектора

Норма вектора x – положительная скалярная величина, вы-

числяемая через его компоненты xi , i 1 n и явно или косвенно

характеризующая его длину. Как и длина вектора, она должна удовлетворять следующим соотношениям:

x y

(1.1)

Приведем три способа определения нормы вектора. 1. Кубическая норма

куб

max

(1.2)

2. Октаэдрическая норма

окт

(1.3)

3. Сферическая норма

сф

x, x .

(1.4)

Концы множества векторов, нормы которых удовлетворяют ра-

венствам xкуб 1, xокт 1 и xсф 1 , нарисуют в n-мерном пространстве поверхности, соответственно, n-мерного куба, n-мерного октаэдра и n-мерной сферы. Это обстоятельство и объясняет их название.

Легко проверить, что все указанные нормы удовлетворяют трем соотношения (1.1).

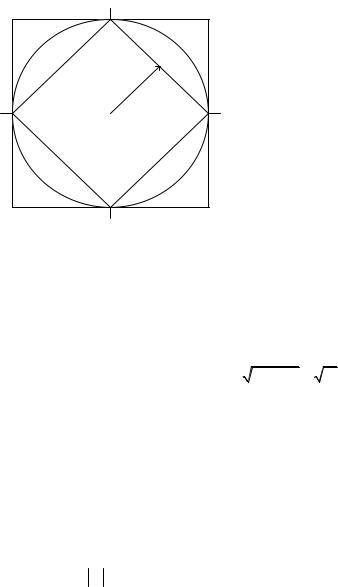
Рис. 1.1. Куб, октаэдр и сфера

Из рис. 1.1 (на котором для двумерного случая построены куб, октаэдр и сфера, соответствующие уравнениям: xкуб 1, xокт 1

и xсф 1 ) видно, что для любого вектора x между этими нормами выполняются следующие соотношения: xокт xсф xкуб .

Справедливость соотношения легко подтверждается на примере

конкретного

вектора x 1,2, 3 ,

для

которого соответствующие

нормы равны

куб 3 ,

окт 6 и

сф

1 4 9 14 3,74 .

Замечание. Из равенства норм двух векторов не следует равенство самих векторов, в товремя как равные вектора всегда имеют равные нормы.

Приведем алгоритмы вычисления двух норм xкуб и xокт (по-

скольку они одновременно демонстрируют, как можно найти максимальное значение и сумму любой последовательности чисел).

1.norm 0 for i 1, n

{

buf xi

if buf norm then norm buf

}

2.norm 0 for i 1, n

{

norm norm xi

}

1.2. Норма матрицы

Норма матрицы A – положительная скалярная величина, которая устанавливает соответствие между нормами исходного вектора x и вектора, являющегося результатом воздействия на ис-

ходный вектор матрицы Ax . При этом в зависимости от критерия, используемого для нахождения нормы матрицы:

sup

определяются два вида норм – согласованная и подчиненная (наименьшая из всех согласованных).

Выведем нормы матрицы подчиненные, соответственно, кубической, октаэдрической и сферической нормам вектора.

куб max

Aij xj

max

Aij

max

Aij

куб

max

Aij

Отсюда

куб max

Aij

(1.5)

окт

Aij xj

Aij

max

Aij

окт max

Aij

Отсюда

max

окт

Aij

(1.6)

сф2 (Ax, Ax) (x, AT Ax) …

Матрица AT A – симметричная и положительно определенная

(так как (AT A)T AT (AT )T AT A и (AT Ax, x) (Ax, Ax) 0 ). По-

этому она имеет полную линейно независимую систему собственных векторов xi , i 1 n , а ее собственные числа – действительные и положительные: 1 2 ... n 0 . Представим произвольный

вектор x в виде разложения по этим векторам x ci xi

и подста-

вим его в верхнее скалярное произведение

ci xi , ci AT Axi

ci xi , ci i xi

ci xi ,

ci xi

...

1(x, x) 1 x2сф .

Отсюда

A	сф 1 .	(1.7)

Замечание. Поскольку для симметричной матрицы AT A A2 , то 1 12 и

Aсф 1 .

В качестве примера нормы матрицы, согласованной со сферической нормой вектора, приведем евклидову норму

евк

Aij2 .

Она

связана

со сферической

нормой

следующим образом:

сф

евк .

Это соотношение подтверждается примерами, пред-

ставленными на рис. 1.2 и 1.3.

Замечание. Приведенные ниже неравенства

max

nmax

куб

max

nmax

окт

n2 max A2

nmax

евк

1 i ( AT A)ii

Aki Aki n2 (max

Aij

)2 ,

устанавливают нижнюю и верхнюю границы для всех указанных норм

n max

Aij

i, j

где 1 – максимальное по модулю собственное число матрицы. Учтено, что сумма

собственных значений матрицы равна ее следу.

На практике выход значения нормы матрицы за пределы этого интервала указывает на то, что норма матрицы определена неверно. Кроме того, эти границы позволяют грубо оценить само значение нормы матрицы.

В заключение приведем алгоритмы вычисления кубической нормы матрицы (для октаэдрической нормы в этом алгоритме необходимо поменять местами индексы в операторах цикла) и

компоненты матрицы B AT A , которая используется при определении сферической нормы матрицы.

куб

max

Aij

norm 0 for i 1, n

{

sum 0 for j 1, n

{

sum sum Aij

}

if sum norm then norm sum

}

2. Bij AikT Akj Aki Akj ; i 1,n; j 1,n :

for i 1, n

{

for j 1, n

{

Bij 0

for k 1.n

{

Bij Bij Aki Akj

}

На рис. 1.2 показан скриншот программы, позволяющей вычислять четыри введенные выше нормы матрицы. Для расчета сферической нормы необходимо предварительно умножить матрицу на транспонированную, а затем методом вращения найти все собственные числа полученной симметричной положительно определенной матрицы. Собственные числа этой матрицы формируются на месте ее диагональных компонент (см. рис. 1.2). Метод вращения описывается в разд. 3.7.

Дополнительно приведем листинг (см. рис. 1.3) функций и подпрограмм для математического пакета Maxima, которые дублируют вычисления, отображенные на рис. 1.2. Результаты их исполнения представлены на рис. 1.4 и 1.5.

1 / 261 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке Литература