
МОСКОВСКИЙ ИНСТИТУТ ЭЛЕКТРОННОЙ ТЕХНИКИ
Институт системной и программной инженерии и информационных технологий (Институт СПИНТех)
Лабораторная работа № 1 по курсу «Интеллектуальные системы – Статистическое обучение»
Линейная регрессия как задача контролируемого (индуктивного) обучения
Выполнил: Баранов В.С. гр.ПИН-11М
Проверил преподаватель: проф., д.ф.-м. н. Рычагов М.Н.
Москва, МИЭТ, 2025 г.
Цель работы
Изучить и реализовать на практике алгоритмы линейной регрессии для задач с одной и несколькими переменными. Освоить метод градиентного спуска для минимизации функции стоимости, а также изучить альтернативный метод нормальных уравнений. Разработать интерактивное веб-приложение для визуализации и анализа данных с помощью реализованных алгоритмов.
Краткие теоретические сведения
Линейная регрессия — это метод моделирования зависимости между зависимой переменной y и одной или несколькими независимыми переменными X путем построения линейной модели.
Гипотеза (Hypothesis): h_θ(x) = θ^T * X = θ x + θ x + ... + θ x (где x = 1)
Функция стоимости (Cost Function): Для оценки точности модели используется функция стоимости J(θ), обычно — метод наименьших квадратов: J(θ) = (1 / 2m) * Σ(h_θ(x^(i)) - y^(i))² Градиентный спуск (Gradient Descent): Итеративный алгоритм для поиска минимума функции стоимости. Параметры θ обновляются на каждом шаге: θ_j := θ_j - α * (1 / m) * Σ(h_θ(x^(i)) - y^(i)) * x_j^(i)где α — скорость обучения
(learning rate).Нормальные уравнения (Normal Equations):Аналитический метод нахождения θ без итераций: θ = (X^T * X)^(-1) * X^T * y
Ход работы
Врамках лабораторной работы было создано интерактивное веб-приложение
сиспользованием библиотеки Streamlit, которое реализует и визуализирует все ключевые этапы, описанные в методических указаниях.
Реализованные функции Код ключевых функций, согласно заданию: codePython
# Функция вычисления стоимости def computeCost(X, y, theta):
m = len(y)
predictions = X.dot(theta)
sqrErrors = (predictions - y) ** 2
J = (1 / (2 * m)) * np.sum(sqrErrors) return J
# Функция градиентного спуска
def gradientDescent(X, y, theta, alpha, num_iters): m = len(y)
J_history = np.zeros(num_iters) for i in range(num_iters):
predictions = X.dot(theta) errors = predictions - y
delta = (1 / m) * (X.T.dot(errors)) theta = theta - (alpha * delta) J_history[i] = computeCost(X, y, theta)
return theta, J_history
#Функция нормализации признаков def featureNormalize(X):
X = X.astype(float)
mu = np.mean(X, axis=0) sigma = np.std(X, axis=0)
sigma[sigma == 0] = 1 # Предотвращение деления на ноль
X_norm = (X - mu) / sigma return X_norm, mu, sigma
#Функция нормальных уравнений
def normalEqn(X, y):
theta = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y) return theta
Часть 1: Простая линейная регрессия
Задача: Прогнозирование прибыли сервисного центра в зависимости от населения города. Данные: service_center.csv
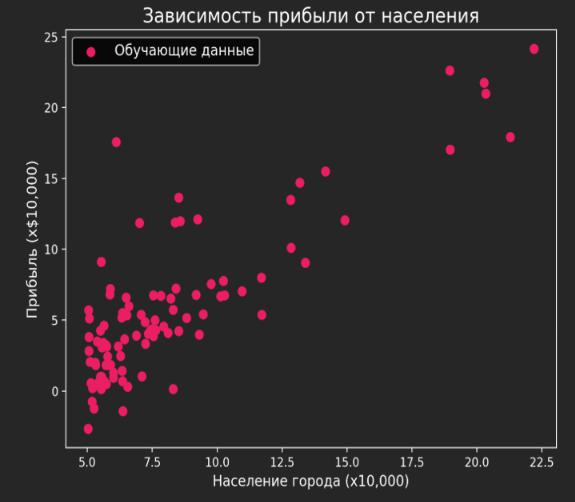
1.1. Визуализация исходных данных
На первом этапе данные были загружены и отображены в виде точечной диаграммы для наглядного представления зависимости.
1.2. Результаты градиентного спуска
Был применен метод градиентного спуска для нахождения оптимальных параметров θ. В результате были получены следующие графики:
Линейный тренд: показывает, как построенная модель соответствует исходным данным.
Сходимость функции стоимости: показывает, как ошибка модели уменьшалась с каждой итерацией, что свидетельствует о корректной работе алгоритма.
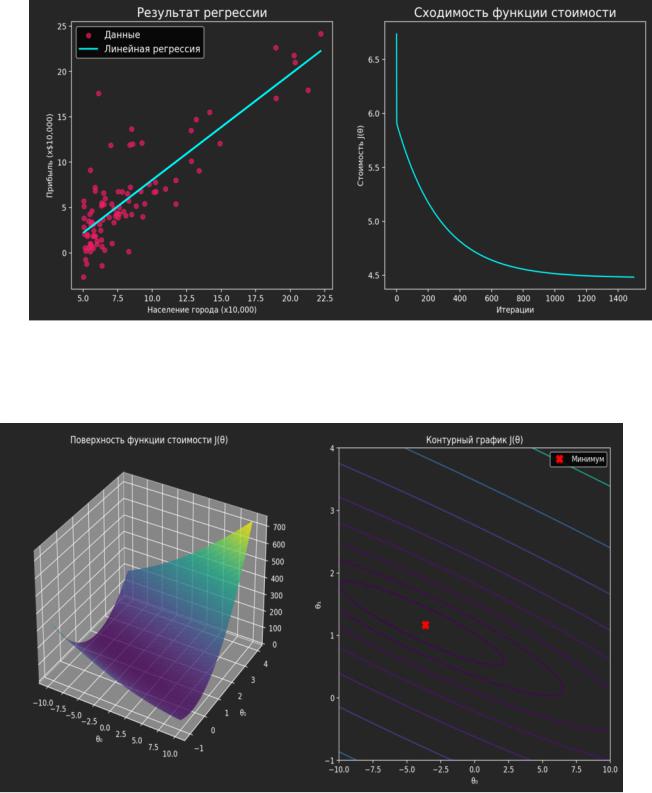
1.3. Визуализация функции стоимости J(θ)
Для глубокого понимания процесса оптимизации была визуализирована сама функция стоимости в 3D и в виде контурного графика. Красный маркер указывает на найденный минимум, что соответствует оптимальным параметрам θ и θ .
