МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

Кафедра «Теория вероятности и прикладная математика»

Дисциплина «Теория вероятностей и математическая статистика»

Отчёт по лабораторной работе №1

на тему

Описательная статистика

Вариант 19

Выборка: {2.22, 1.32, 1.48, 0.68, 2.3, 1.37, 1.51, 1.43, 1.82, 2.62, 1.75, 1.54, 2.25, 1.07, 1.44, 1.4, 1.31, 1.12, 1.16, 0.88, 1.07, 1.24, 1.49, 2.03, 1.84, 1.22, 1.72, 1.75, 1.46, 1.6}

Задание 1

С помощью критериев согласия Пирсона и Колмогорова проверить гипотезу о том, что выборка из задания 2 лабораторной работы 1 имеет нормальное распределение.

Задание 2

Для выборки из задания 2 лабораторной работы 1 найти интервальные оценки параметров нормального распределения.

Выполнение Задания 1

xi	[0,52;0,84)	0,84;1,16)	[1,16;1,48)	[1,48;1,8)	1,8;2,12)	[2,12;2,62]
ni	1	4	10	8	3	4
pi	0.03	0.13	0.33	0.27	0.10	0.13
hi	0.09375	0.40625	1.03125	0.84375	0.3125	0.40625
ti	0.68	1	1.32	1.64	1.96	2.37

Объединю крайние интервалы с соседними, чтобы получить n_i > 5

xi	[0,52;1,16)	[1,16;1,48)	[1,48;1,8)	1,8; 2,62)
ni	5	10	8	7
pi	0.16	0.33	0.27	0.23
hi	0.5	1.03125	0.84375	0,71875
ti	0.84	1.32	1.64	2.21

Выборочное среднее:

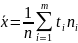
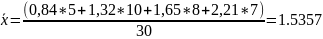
Выборочная смещённая дисперсия:

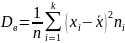
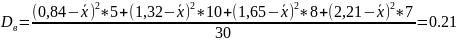
Выборочное стандартное отклонение:

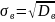
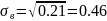
Вероятность попадания в интервал:

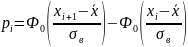
p₁ =

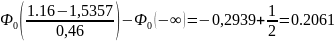
p₂ =

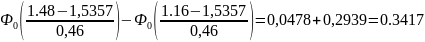
p₃ =

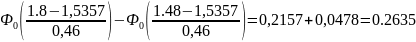
p₄ =

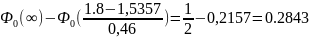
xi	[0,52;1,16)	[1,16;1,48)	[1,48;1,8)	1,8; 2,62)
ni	5	10	8	7
ni′=npi	6.183	10.251	7.905	8.529

Критерий Пирсона:

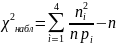
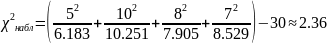
Количество степеней свободы: k = m – r – 1 = 1

α = 0,01

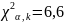
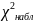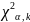< , гипотезу принимаем

Критерий согласия Колмогорова:

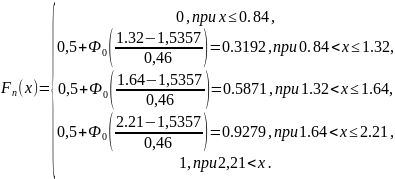
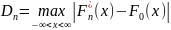
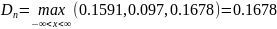
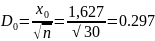
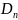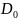< , гипотезу принимаем

Выполнение Задания 2

;

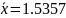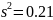
α = 1 – γ = 0,01; γ = 0,99

Доверительный интервал математического ожидания:

Для γ = 0,99 и 29 (n – 1) степеней свободы по таблицам распределения Стьюдента находим t_{α, n – 1} = 2,756

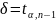
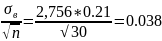
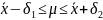
1.497 < 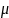< 1.574

Доверительный интервал математического дисперсии:

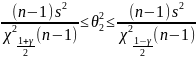
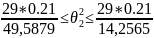
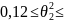0,43