
Лаб16
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра «Теории электрических цепей»
Дисциплина «Электротехника»
Отчёт по лабораторной работе №16
на тему
«Исследование резонансных явлений в пассивном и активном последовательном колебательном контуре»
Выполнил:
Проверил:
Цель работы
С помощью программы Micro-Cap исследовать характеристики одиночного последовательного пассивного и активного колебательного контура при различных добротностях.
Предварительный расчет
Исходные данные:
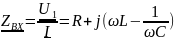 – комплексное входное сопротивление
контура;
– комплексное входное сопротивление
контура;
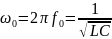 – резонансная частота контура;
– резонансная частота контура;
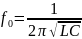 – частота;
– частота;
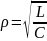 –
характеристическое
сопротивление;
–
характеристическое
сопротивление;
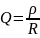 – добротность;
– добротность;
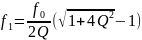 – нижняя
граничная частота;
– нижняя
граничная частота;
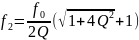 – верхняя
граничная частота;
– верхняя
граничная частота;
П = f2 – f1 – абсолютная полоса пропускания;
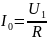 – модуль
входного тока при резонансе;
– модуль
входного тока при резонансе;
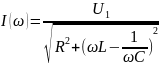 – резонансная
кривая тока при условии, что меняется
только частота источника напряжения.
– резонансная
кривая тока при условии, что меняется
только частота источника напряжения.
По предварительному расчету U1 = 1 B, f0 = 4,8 кГц, С = 10 нФ, L = 0,11 Гн |
Получено экспериментально |
|||||||||||||
R, Ом |
|
Q |
f1, кГц |
f2, кГц |
П, кГц |
I0, А |
f0, кГц |
f0, кГц |
I0, А |
f1, кГц |
f2, кГц |
П, кГц |
Q |
|
160 |
3316,6248 |
20,73 |
4,684 |
4,916 |
0,232 |
0,006 |
4,8 |
4,8 |
0,006 |
4,684 |
4,916 |
0,232 |
20,73 |
|
640 |
3316,6248 |
5,18 |
4,358 |
5,285 |
0,927 |
0,0015 |
4,8 |
4,8 |
0,0015 |
4,358 |
5,285 |
0,927 |
5,18 |
|
Гиратор |
||||||||||||||
По предварительному расчету U1 = 1 B, f0 = 5 кГц, С2 = 1 мкФ, G = 0,1 См |
Получено экспериментально |
|||||||||||||
R, Ом |
С1, мкФ |
f0, кГц |
||||||||||||
0,1 |
10,14 |
5 |
||||||||||||
Таблица 1 – результаты эксперимента
Расчет для пассивного последовательного колебательного контура

Рис. 1.1 Расчет величины индуктивности

Рис. 2.1 Расчет величин при R = 160 Ом

Рис. 3.2 Расчет величин при R = 640 Ом
Расчет для гиратора

Рис. 2 Расчет для гиратора
Построение графика зависимости входного сопротивления от частоты

Рис. 3.1 Написание кода для графика
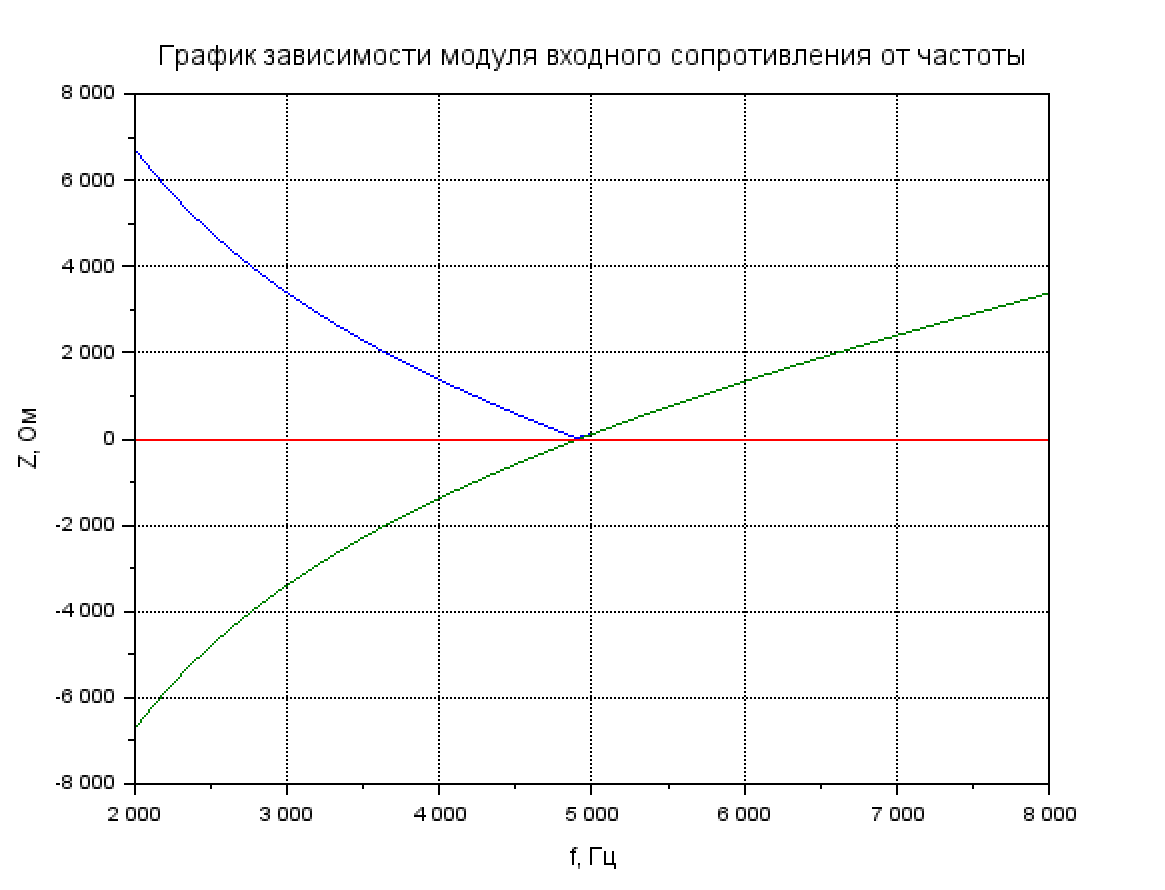
Рис. 3.2 График зависимости входного сопротивления от частоты при R = 160 Ом
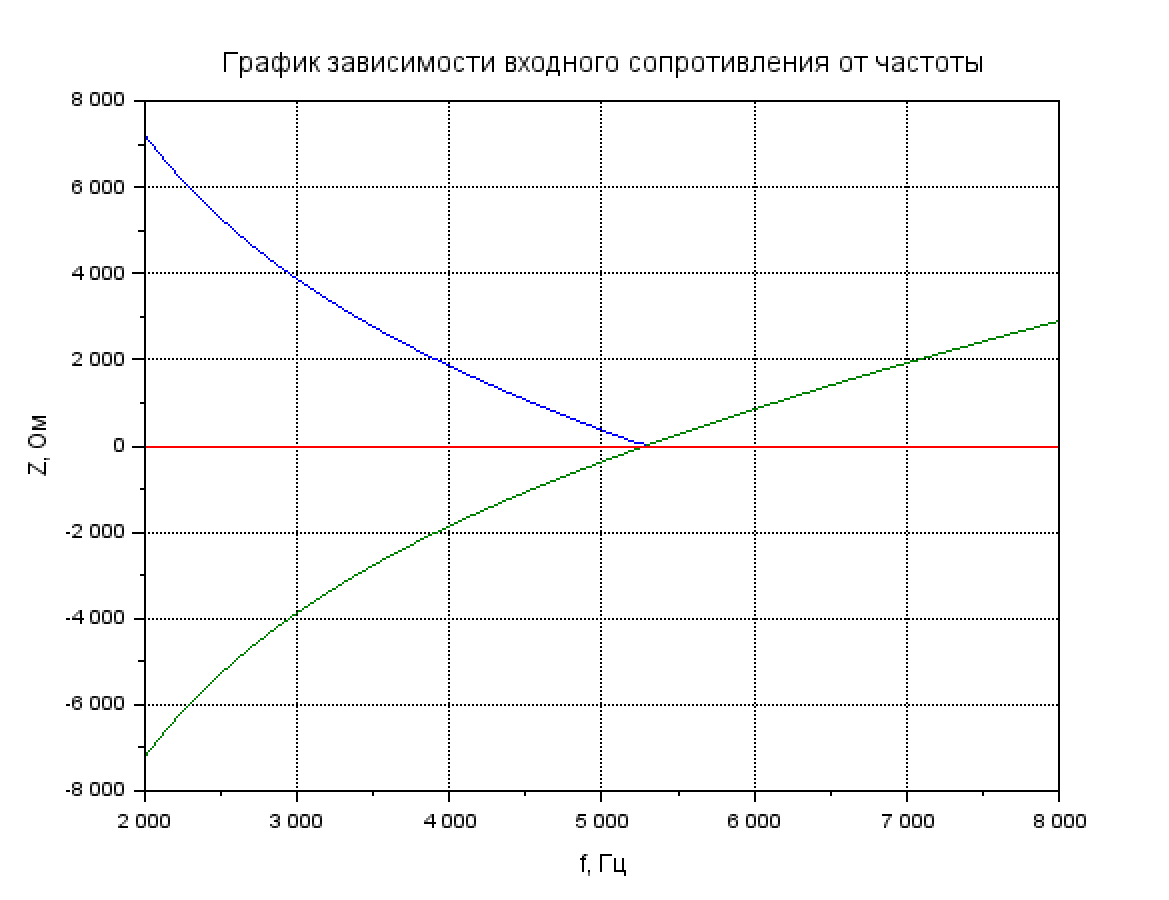
Рис. 3.3 График зависимости входного сопротивления от частоты при R = 640 Ом
Построение графика зависимости фазы входного сопротивления от частоты

Рис. 4.1 Написание кода для графика
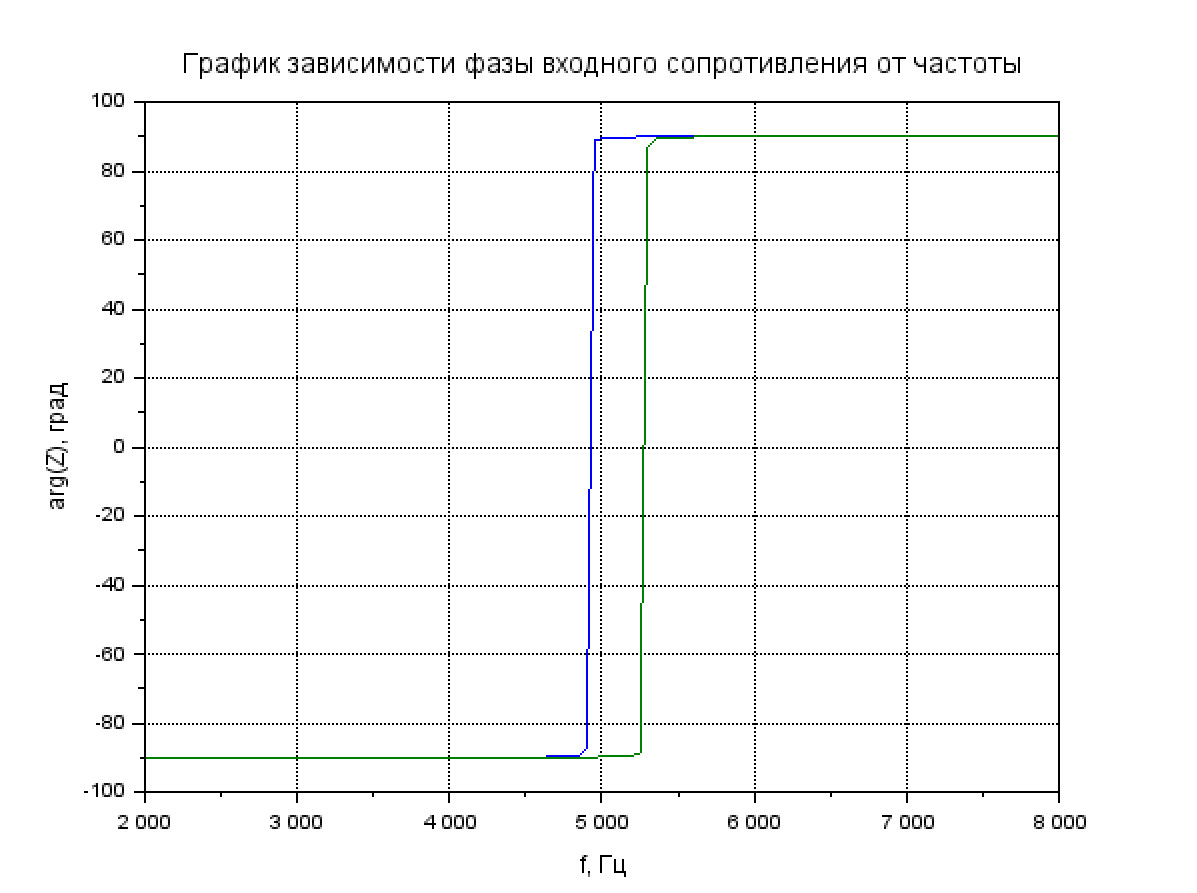
Рис. 4.2 График зависимости фазы входного сопротивления от частоты
Построение графика зависимости входного тока от частоты

Рис. 4.1 Написание кода для графика
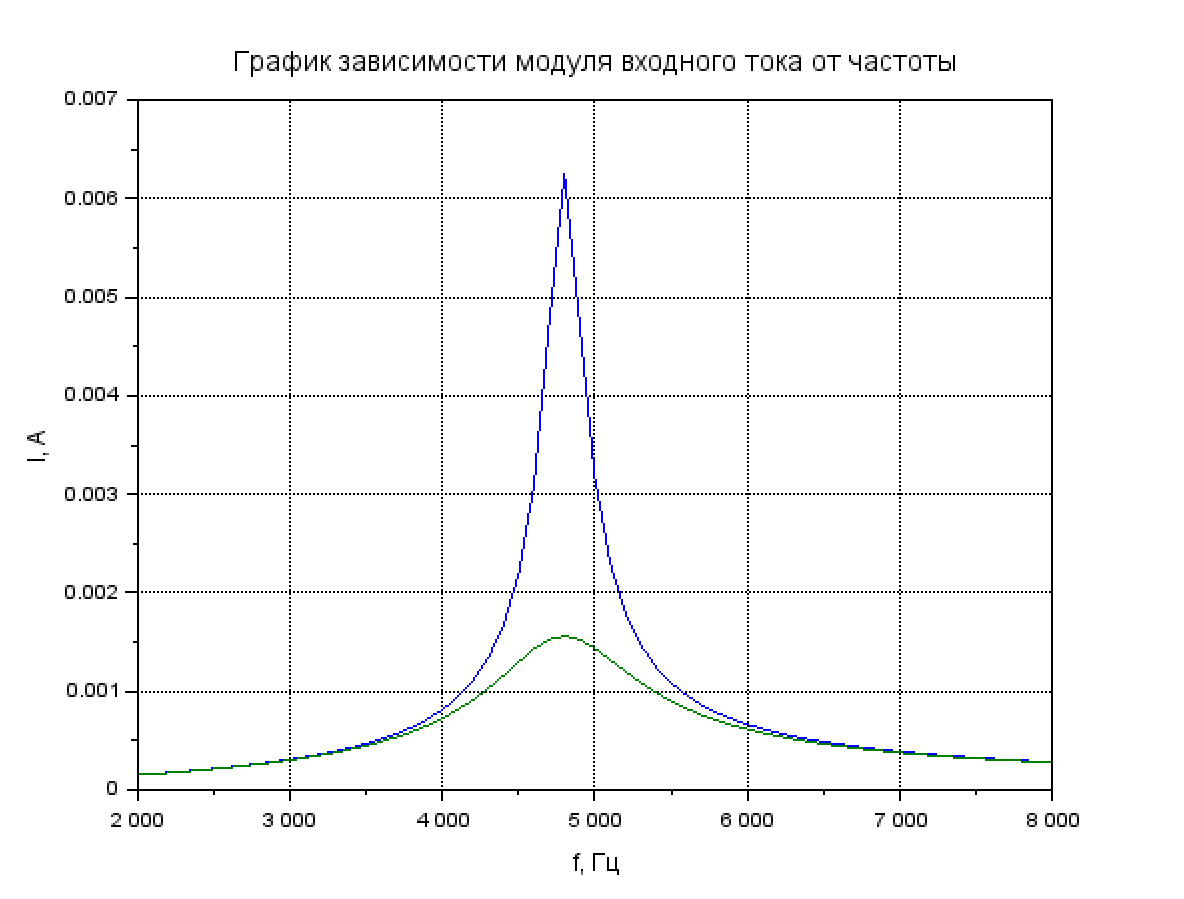
Рис. 4.2 График зависимости входного тока от частоты
Экспериментальный расчет
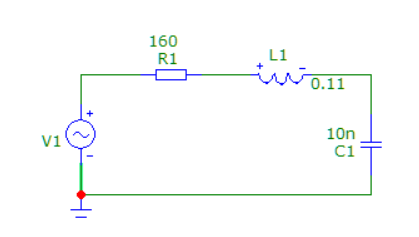
Рис. 5 Схема пассивного колебательного контура
Зависимость модуля входного сопротивления от частоты
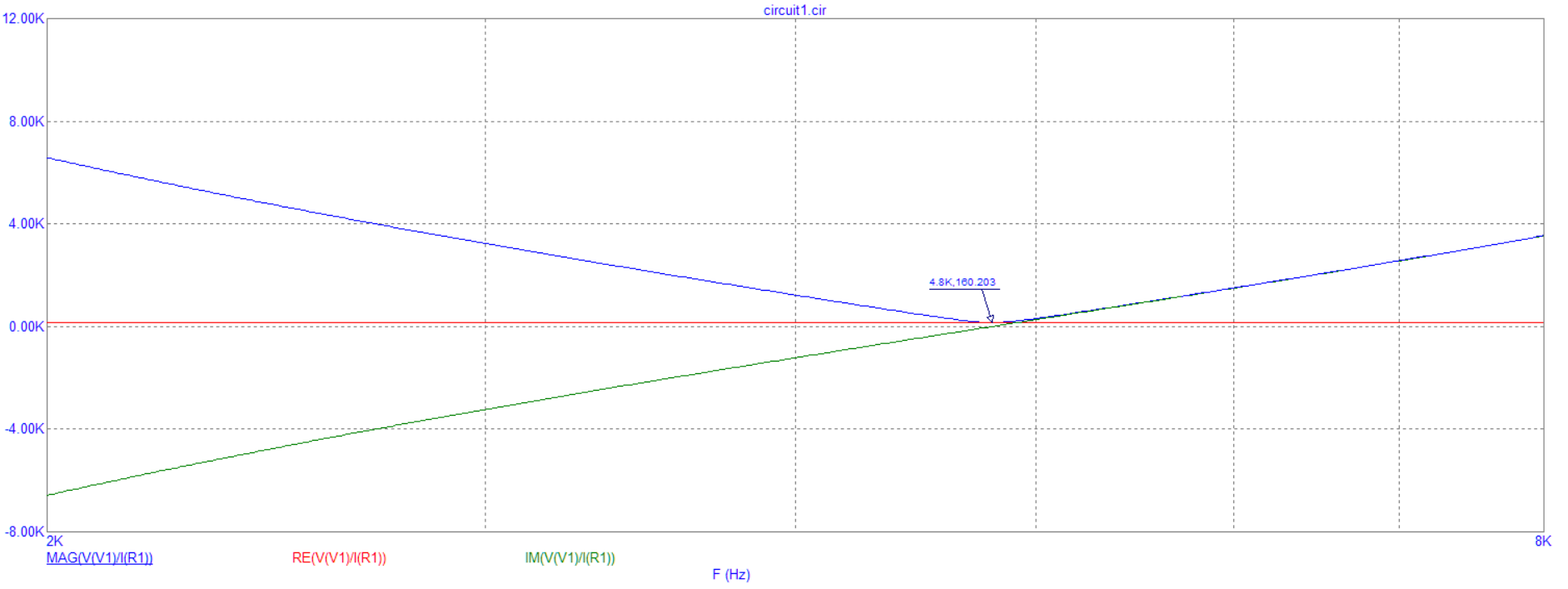
Рис. 6.1 График зависимости модуля входного сопротивления от частоты при R = 160 Ом
Вывод: при увеличении частоты до резонансной, входное сопротивление уменьшается, затем повышается.
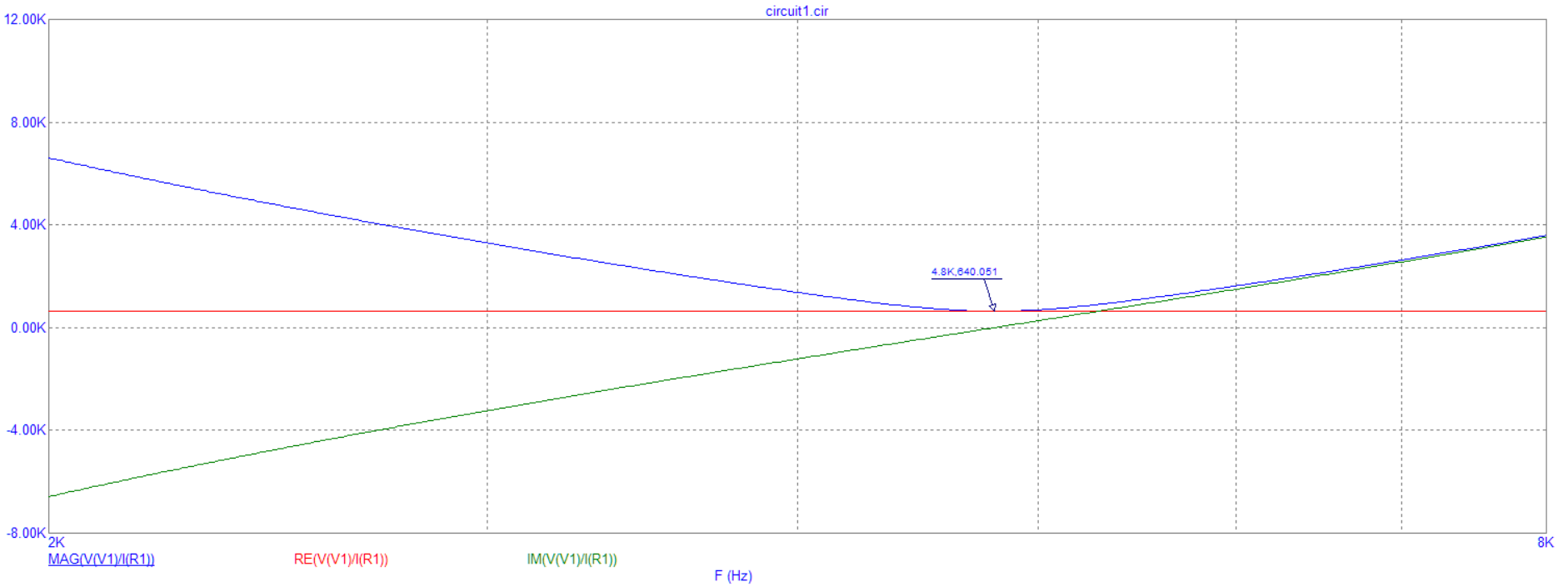
Рис. 6.2 График зависимости модуля входного сопротивления от частоты при R = 640 Ом
Вывод: при увеличении частоты до резонансной, входное сопротивление уменьшается, затем повышается.
Зависимость фазы входного сопротивления от частоты
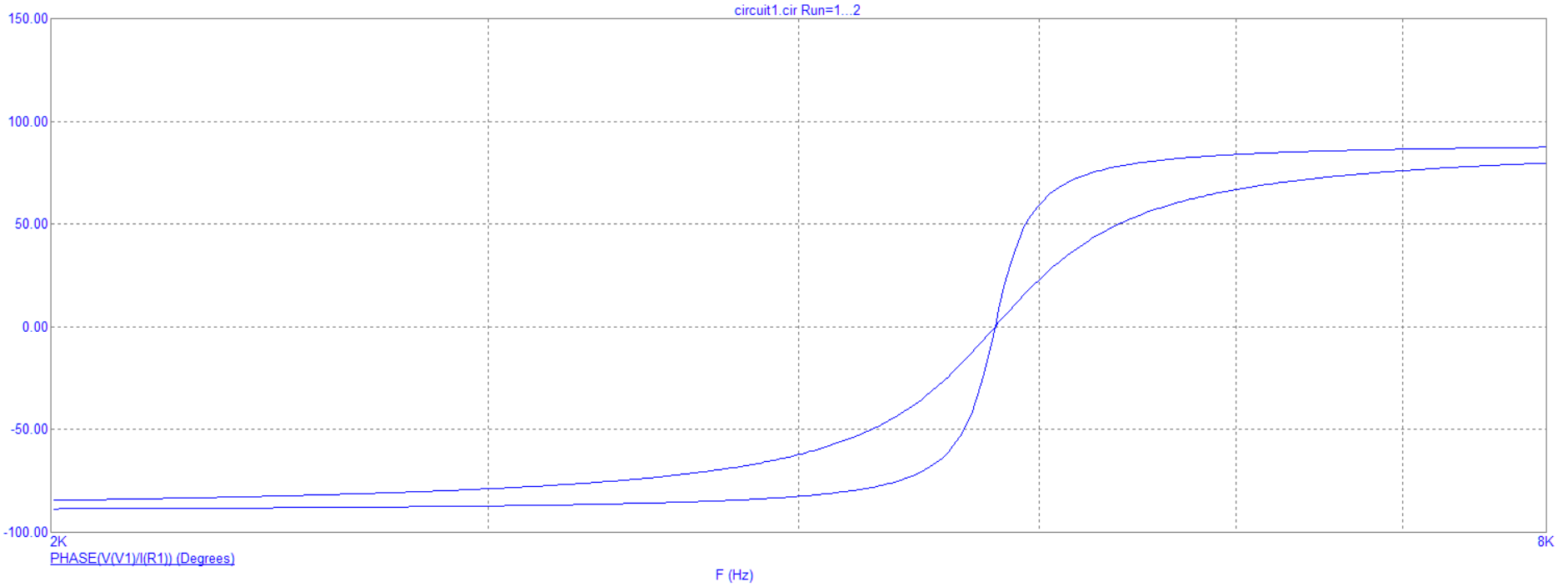
Рис. 7 График зависимости фазы входного сопротивления от частоты
Вывод: при увеличении частоты до резонансной, фаза входного сопротивления растет, затем уменьшается.
Зависимость модуля входного тока от частоты
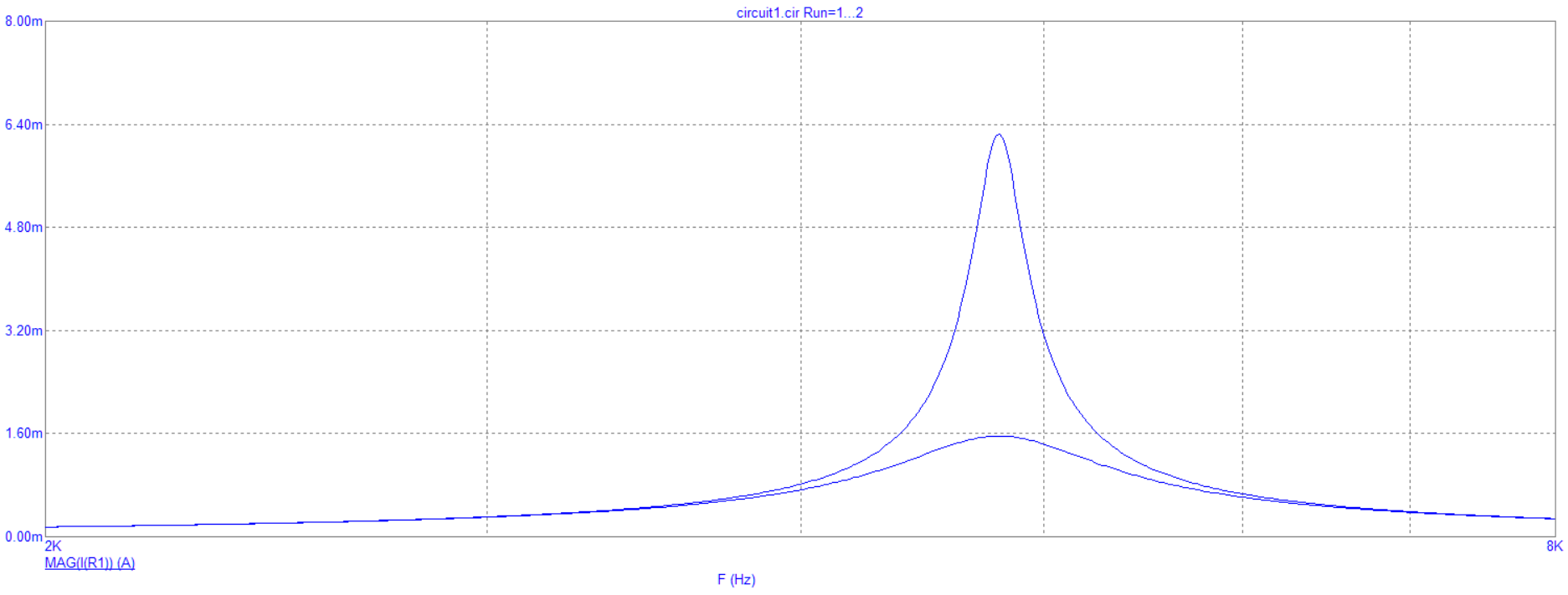
Рис. 8.1 График зависимости модуля входного тока от частоты
Вывод: при увеличении частоты модуль входного тока образует резонансную кривую с различной амплитудой в зависимости от резистора.
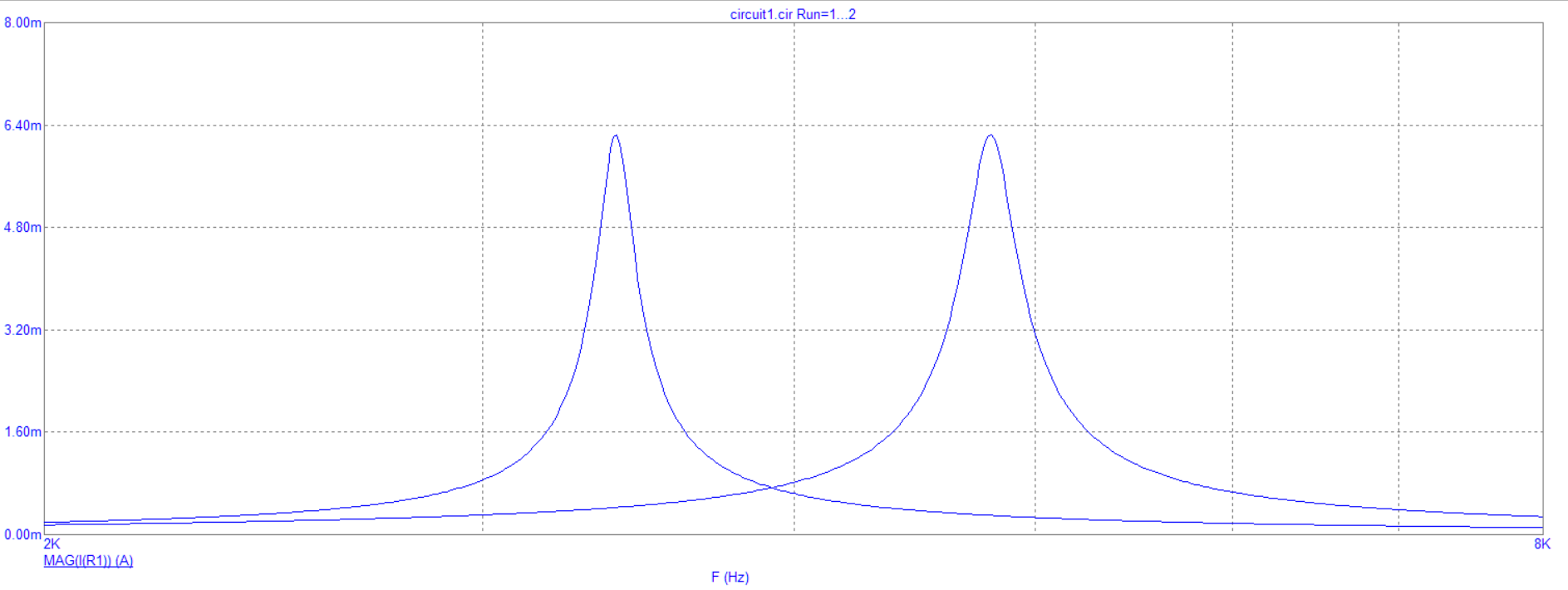
Рис. 8.2 График зависимости модуля входного тока от частоты при изменении параметров индуктивности
Вывод: при увеличении частоты модуль входного тока образует резонансные кривые с различной амплитудой в зависимости от индуктивности.
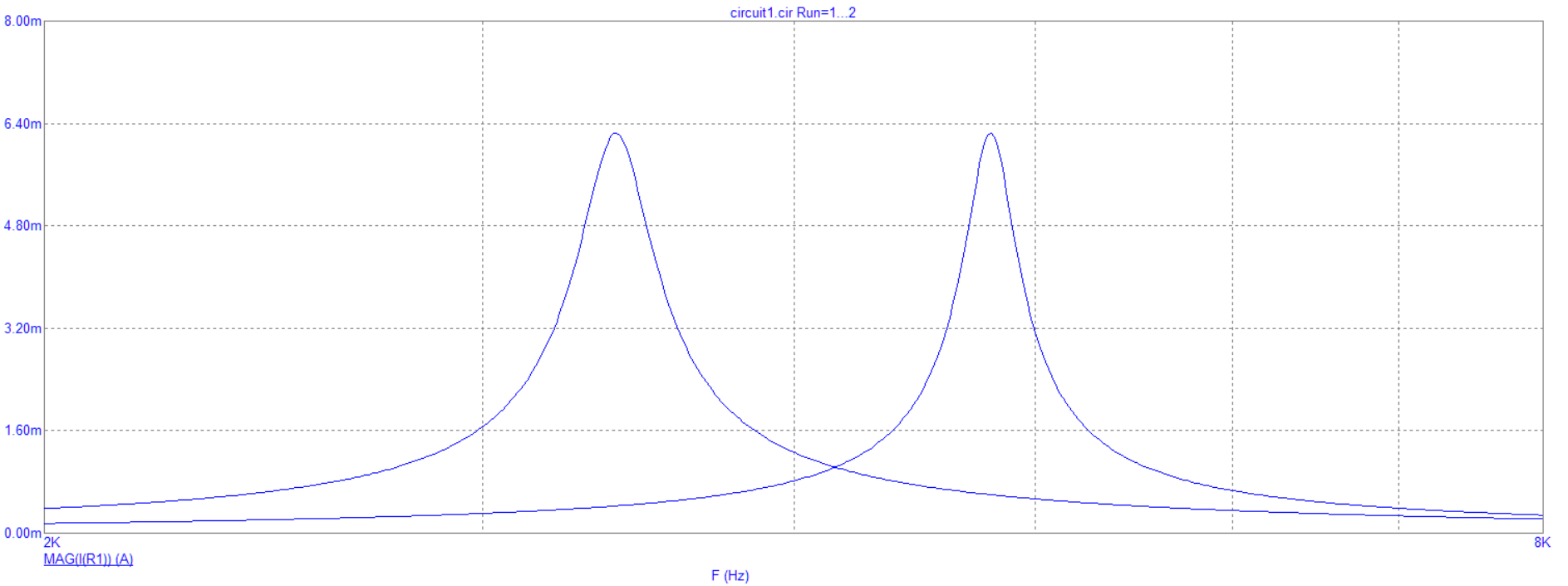
Рис. 8.3 График зависимости модуля входного тока от частоты при изменении параметров емкости
Вывод: Вывод: при увеличении частоты модуль входного тока образует резонансные кривые с различной амплитудой в зависимости от емкости.
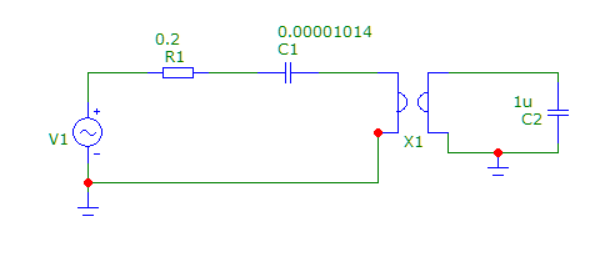
Рис. 9 Схема с гиратором
Зависимость модуля тока от частоты в схеме с гиратором
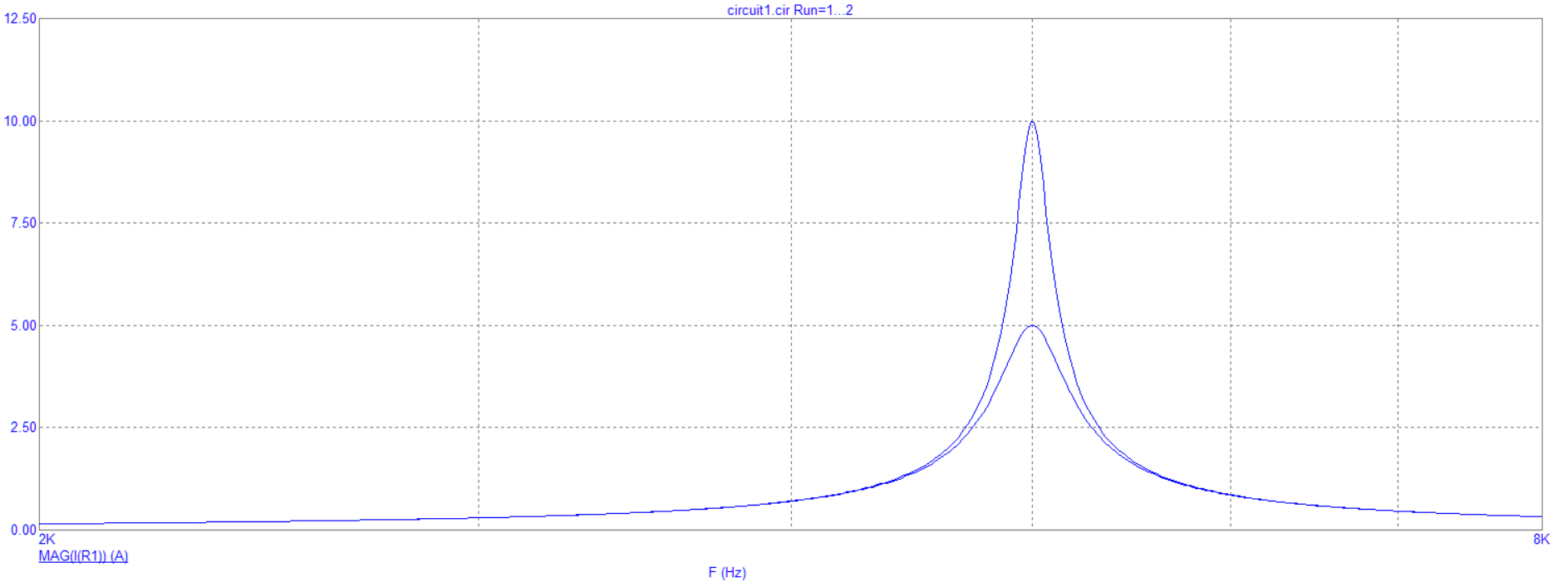
Рис. 10 График зависимости модуля входного тока от частоты в схеме с гиратором
Вывод: при увеличении частоты модуль входного тока образует резонансную кривую с различной амплитудой в зависимости от резистора.
Вывод
Данные и графики, полученные в результате машинного эксперимента в программе Micro-Cap, полностью совпадают с данными и графиками, полученными в результате предварительного расчёта.
Вопросы для самопроверки
Что такое входная функция и что такое передаточная функция цепи? Какова их физическая сущность?
Дайте определение входной АЧХ, входной ФЧХ. передаточной АЧХ, передаточной ФЧХ цепи?
Как, зная значение параметров элементов, рассчитать граничную частоту для неразветленной RL, RC цепей.
На примерах схем RL, RC цепи, покажите, что в неразветленной цепи первого порядка модуль входного комплексного сопротивления на граничной частоте равен R
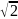 ,
а модуль аргумента входного комплексного
сопротивления и модуль аргумента
комплексного коэффициента передачи
равно по 45 градусов каждый
,
а модуль аргумента входного комплексного
сопротивления и модуль аргумента
комплексного коэффициента передачи
равно по 45 градусов каждыйКак по графику входной АЧХ неразветлённой цепи первого порядка определить граничную частоту?
Как по графику входной ФЧХ неразветленной цепи первого порядка определить граничную частоту?
Как по графику передаточной ФЧХ неразветленной цепи первого порядка определить граничную частоту?
Входная комплексная функция цепи – это или зависимость комплексного сопротивления от частоты:
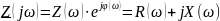 ,
,
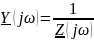
относительно двух заданных входных зажимов.
Входная АЧХ – зависимость модуля входного комплексного сопротивления от частоты.
Входная ФЧХ – зависимость аргумента входного комплексного сопротивления от частоты.
Передаточная АЧХ – зависимость модуля входного комплексного коэффициента передачи от частоты.
Передаточная ФЧХ – зависимость аргумента комплексного коэффициента передачи от частоты.
Для RL цепи: XL=R, ωгрL=R, следовательно, ωгр =
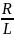 ,
или fгр=
,
или fгр=
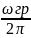 =
=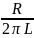 ;
;
Для
RС
цепи: XC=R,
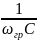 =R,
следовательно, ωгр
=
=R,
следовательно, ωгр
=
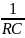 ,
или fгр=
=
,
или fгр=
=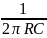 ;
;
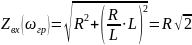 ;
;
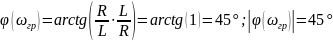 ;
;
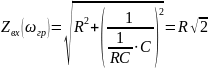 ;
;
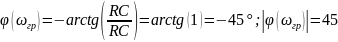
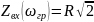 .
.Определить граничную частоту (
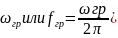 можно по соответствующему значению
модуля аргумента входного сопротивления
можно по соответствующему значению
модуля аргумента входного сопротивления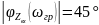 .
.Определить граничную частоту ( можно по соответствующему значению модуля аргумента комплексного коэффициента передачи
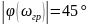 .
.

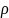 ,
Ом
,
Ом