
Физика тесты
.pdf
1)Сумма двух случайных событий (А+B) — это такое событие, при котором происходит СОБЫТИЕ А ИЛИ СОБЫТИЕ B
2)Интервальная оценка параметров генеральной совокупности характеризуется ДВУМЯ числами и используется, если выборка
МАЛОГО объема
3)Заряд случайных величин 20 22 24 26 28 30 32 медиана этого ряда равна 26 (Медиану смотрим по среднему числу в ряде)
4)При использовании параметрических критериев в случае, когда наблюдаемое значение критерия меньше его критического значения
СЧИТАЮТ ВЕРНОЙ НУЛЕВУЮ ГИПОТЕЗУ
5)В ящике 50 шаров: 10 красных, 15 синих, 25 белых. Вероятность того, что вынутый наугад шар будет синий РАВНЯЕТСЯ 0,3 (белый цвет не считаем за цветной шарик, поэтому 15 делим на 50)
6)Слово «МЕДИЦИНА». Наугад выбирается одна буква. Вероятность того, что эта буква будет «Ч» РАВНА 0 (буквы ч нет в слове медицина)
7)P (A/B)- это вероятность события A при условии, что событие B
произошло
8)Закон сложения вероятностей для двух несовместных событий:
P (A ИЛИ B) =P(A)+P(B)
9)Вероятность того, что исследуемая величина выйдет за назначенный ей интервал, называется УРОВНЕМ ЗНАЧИМОСТИ
10)Обозначение случайных событий- A, B, C, D….
11)Вероятность того, что пациент A в течение часа потребует внимания медсестры равна 0,7. Пациент B потребует внимания с вероятностью 0.9, а пациент C потребует внимания медсестры с вероятностью 0.5. Найдите вероятность того, что хотя бы один из пациентов не потребует внимания медсестры в течение часа.
РЕШЕНИЕ: P= P(A) * P(B) * P(C) = 0,7 * 0,5 * 0,9 = 0,315 P= 1-0,315= 0,685
12)В ящике 10 шаров: 5 белых и 5 синих. Вынимание наугад одного синего шара и одного белого шара — это события НЕСОВМЕСТНЫЕ
13)Для проверки гипотез о равенстве средних из параметрических критериев используют критерий СТЬЮДЕНТА
14)Выборка, элементы которой отобраны из генеральной совокупности случайным образом, называется РАНДОМИЗИРОВАННОЙ
15)При бросании игрального кубика возможно шесть исходов: выпадение 1, 2, 3, 4, 5, 6 очков. Вероятность появления четного или кратного трём числа равна 2/3
РЕШЕНИЕ: = (четные: 2, 4, 6 и кратные: 3 и 6)
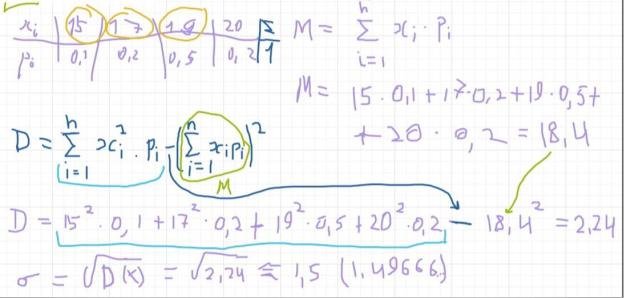
16) Невозможное событие никогда не происходит
17) Непрерывная случайная величина: АРТЕРИАЛЬНОЕ ДАВЛЕНИЕ
ПАЦИЕНТА В ТЕЧЕНИЕ СУТОК
18) Произведение двух случайных событий (A*B) — это такое событие, при котором происходит СОБЫТИЕ A И СОБЫТИЕ B
19) Доверительная вероятность может принимать значение 0,95
20) Дискретная случайная величина задана законом распределения
Xi 15 17 19 20 Pi 0,1 0,2 0,5 0,2
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ= 18,4 ДИСПЕРСИЯ= 2,24 СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ= 1,5
Прикладываю свои каракули-решения (ВСЕ ЗАДАНИЯ ПОХОЖИ)
Другой вариант (не ебу какой).
1)Правило, позволяющие основываясь на выборочных данных принять или отвергнуть альтернативную гипотезу, называется СТАТИСТИЧЕСКИЙ
КРИТЕРИЙ
2)Параметрический статистический критерий определяется
ПАРАМЕТРАМИ ДАННОЙ СОВОКУПНОСТИ
3)Критическое значение критерия зависит от ЧИСЛА СТЕПЕНЕЙ
СВОБОДЫ И УРОВНЯ ЗНАЧИМОСТИ
4)При проверке гипотезы о соответствии закона распределения НЗР, наблюдаемое значение критерия меньше критического, можно сделать вывод:
ДАННЫЕ ЗАПИСЫВАЮТСЯ НОРМАЛЬНЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ

5)Интегральная функция распределения вероятностей F(X) существует для
ЛЮБЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
6)Применение параметрических критериев для проверки статистических гипотез возможно, если экспериментальные данные имеют НОРМАЛЬНЫЙ
ЗАКОН РАСПРЕДЕЛЕНИЯ
7)Гипотеза, заключающаяся в том, что сравниваемые генеральные параметры различаются значимо ОБОЗНАЧАЕТСЯ H1 И НАЗЫВАЕТСЯ
АЛЬТЕРНАТИВНОЙ
8)В математической статистике альтернативную гипотезу обозначают: H1
9)Из следующих оценок параметров генеральной совокупности несмещенной является ВЫБОРОЧНАЯ СРЕДНЯЯ
10)Гипотеза H1, противоречащая H0 и заключающиеся в том, что сравниваемые генеральные параметры различаются, называется
АЛЬТЕРНАТИВНАЯ
11)Справедливость нулевой гипотезы проверяется СРАВНЕНИЕМ
НАБЛЮДАЕМОГО ЗНАЧЕНИЯ КРИТЕРИЯ И КРИТИЧЕСКОГО
12)Экспериментальное значение критерия определяется следующим образом:
По соответствующей формуле
13)Вероятность случайного события: < < (Почему не меньше и равно?)
14)Слово «МЕДИЦИНА» наугад выбирается одна буква. Вероятность того, что эта буква «И» равна 0,25 (всего букв-8, но буква «и» повторяется 2 раза,
поэтому = = ,
15)Дискретной случайной величиной НЕ является АРТЕРИАЛЬНОЕ ДАВЛЕНИЕ ПАЦИЕНТА (лол, что? Оно меняется непрерывно, т.е. это функция с множеством значений, а вот рост студента не дискретная)
16)Обозначение случайных величин: X, Y, Z.
17)В коробке 30 таблеток: 10 красных, 5 желтых, 15 белых. Вероятность
вынуть цветную таблетку равна (по аналогии с шариками, белый цвет
не считаем)
18)Закон умножения вероятностей для двух зависимых событий:
P (A И B) = P (A)* P(B/A)
19)В случае, если при проверке гипотезы о равенстве средних выяснилось, что наблюдаемое значение критерия ниже критического, можно сделать вывод: РАЗЛИЧИЕ ГЕНЕРАЛЬНЫХ СРЕДНИХ НЕЗНАЧИМО

20)В ящике 10 шаров: 5 белых и 5 синих. Вынимание наугад одного белого шара и вынимание наугад одного синего шара — это события
НЕСОВМЕСТНЫЕ
21)Сумма произведений случайных величин на вероятность их появления называется МАТЕМАТИЧЕСКИМ ОЖИДАНИЕМ
22)80 пробирок находится в ящике. Из них 4 имеют трещины. Определите вероятность того, что вынутые одна за другой две пробирки окажутся с трещинами. Ответ округлите до тысячных. ОТВЕТ: 0,002
23)Теория вероятностей изучает СЛУЧАЙНЫЕ СОБЫТИЯ
24)Величина, определяемая как квадратный корень из выборочной дисперсии,
называется СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ
25)Xi-варианта, ni- частота встречаемости
xi 50 55 60 65 ni 5 27 17 6
Мода этого распределения равна 55 (потому что это число встречается больше всего раз27)
26) Наблюдаемое значение критерия Фишера равно ОТНОШЕНИЮ
ОБЩЕЙ ДИСПЕРСИИ К МЕНЬШЕЙ
Очередной варик:
1)К параметрическим критериям проверки статистических гипотез не относится КРИТЕРИЙ ЗНАКОВ
2)Предположение о равенстве генеральных средних двух генеральных совокупностей, проверяемое по выборкам, называется
(ГИПОТЕТИЧЕСКИМ АНАЛИЗОМ???)
3)Вероятность события «ВСТРЕТИТЬ ДИНОЗАВРА НА УЛИЦЕ» РАВНА
P=0
4)Совокупность случайно отобранных наблюдений (объектов) для
непосредственного изучения называется… (ТОЧНО НЕ ГИСТОГРАММА, НЕ
ГЕН. СОВОКУПНОСТЬ (ВОЗМОЖНО, ВЫБОРКА))

5)Интервал, в котором с той или иной заранее заданной вероятностью находится неизвестный параметр генеральной совокупности, называется
ДОВЕРИТЕЛЬНЫМ ИНТЕРВАЛОМ
6)Выборка — это часть ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
7)При бросании игрального кубика возможно шесть исходов: выпадение 1, 2, 3, 4, 5, 6. Определите вероятность выпадения нечетного числа очков.
Ответ: 0,5
Решение: нечетные числа: 1, 3, 5. Всего-6. 3/6=0,5
8)При подбрасывании кубика выпадет число меньше 7 — это событие
ДОСТОВЕРНОЕ
9)Число степеней свободы для определения критического значения критерия Стьюдента… (не видно на фотке было) = + −
10)Оценка параметра генеральной совокупности, которая определяется одним числом, называется ТОЧЕЧНОЙ
11)При стрельбе по мишени частота попаданий составила 0,7, количество попаданий при… выстрелах равно
ОТВЕТ: 14
12)Разность между наибольшим и наименьшим значениями признака,
называется ВАРИАЦИОННЫЙ РАЗМАХ
13)Вероятность ошибки отвергнуть нулевую гипотезу, если в действительности она… называется УРОВЕНЬ ЗНАЧИМОСТИ
14)Один из критериев, при помощи которого сравнивают генеральные дисперсии: ФИШЕРА
15)Дискретные случайные величины ПРИНИМАЮТ СЧЕТНОЕ ЧИСЛО
ЗНАЧЕНИЙ
Опять другой вариант:
1)Бросают 2 игральных кубика. Какова вероятность того, что на первом кубике выпадет четное число очков, а на второмчисло, меньше 6? Решение: = ,
2)Найти выборочное среднее и выборочную дисперсию по данному распределению:
xi 3 4 5 ni 2 1 3
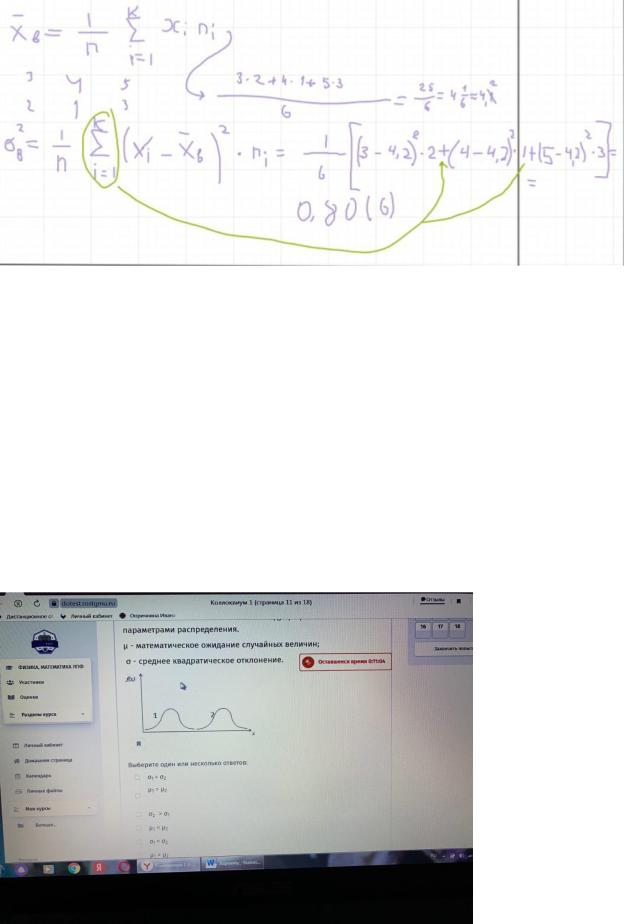
Ответ округлить до десятых.
ОТВЕТ: 4.2 И 0.8
3)Случайная величина измеряется в кг. Математическое ожидание имеет единицы измерения: КГ
4)Математическое ожидание случайной величины характеризует
СРЕДНЕЕ ЗНАЧЕНИЕ
5)Равновозможные события ИМЕЮТ ОДИНАКОВУЮ ВЕРОЯТНОСТЬ (даунская формулировка, не уверен в правильности ответа)
6)Статистическое событие — это совокупность ВАРИАНТ И
СООТВЕСТВУЮЩИХ ИМ ЧАСТОТ
7)Число степеней свободы при определении доверительного интервала для математического ожидания генеральной совокупности: = −
8)Из следующих оценок параметров генеральной совокупности несмещенной является: ВЫБОРОЧНАЯ СРЕДНЯЯ
9)
Ответ: 1 и 4
