Физика тесты

• Для проверки гипотез о равенстве средних из параметрических критериев используют критерий

Стьюдента

• На рисунке приведены две корреляционные зависимости переменной и Х:

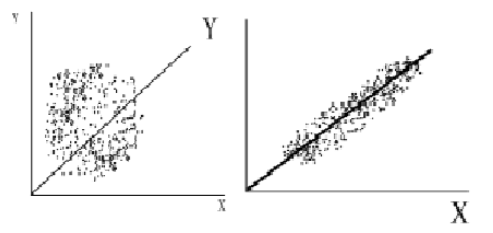
Очевидно, что в случае а:

Коэффициент корреляции должен быть меньше, чем случае б

• Если наблюдаемое значение Т-критерия Стьюдента Тнабл=4,2 , а критическая Ткр =2.3 при 0.05, то можно сделать вывод , что линейная связь между признаками X и Y:

Имеется

• При проверке значимости выборочного коэффициента линейной корреляции выдвигается нулевая гипотеза

r_ген>0

• Если наблюдаемое значение t-критерия Стьюдента t_набл =4,5, а критическое t_кр =2,3 при a ≤ 0,05, r=-0,95 - это означает, что линейная корреляционная связь между признаками:

очень сильная

заметная

• Дана двумерная выборка, коэффициент корреляции которой равен r=-0.85

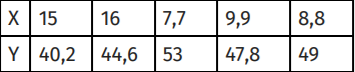
Если все значения переменных Х и Y увеличить на 0.1, то коэффициент корреляции станет равен:

–0,85

• Причина, вызывающая изменения величины результативного признака

Контролируемые и неконтролируемые факторы

• Влияние фактора а на признак х достоверно, если

F_эксп > F_табл (a, f₁, f₂)

• На чем основан дисперсионный анализ.

На разложении общей дисперсии статистического комплекса на составляющие компоненты.

• Найти выборочное среднее и выборочную дисперсию по данному распределению

1.7 и 0.6

• Установите соответствие между названием статистического критерия и его использованием

Критерий Стьюдента: Сравнение выборочных средних

Критерий Пирсона: Сравнение выборочных данных

• Критическое значение критерия зависит от

числа степеней свободы и уровня значимости

• Наблюдаемое значение критерия Фишера всегда

больше либо равно единице

• К параметрическим критериям проверки статистических гипотез не относится

Критерий знаков

• Уровень значимости принимается равным

малому числу (0,001; 0,01, 0,05)

• Число степеней свободы для определения критического значения критерия Стьюдента в задаче проверки гипотезы о равенстве средних значений в выборках определяется по формуле

f=n1+n2-2

• Любое высказывание о генеральной совокупности, проверяемое по выборке, называется

статистическая гипотеза

• При использовании параметрических критериев в случае, когда Кнабл меньше Ккрит,

принимают нулевую гипотезу

• В математической статистике гипотезу обозначают

H

• Коэффициент корреляции r=0. Это говорит о том, что

Линейная корреляционная зависимость отсутствует

• Теснота (сила) линейной корреляционной связи определяется

Величиной коэффициента корреляции

• Если наблюдаемое значение t-критерия Стьюдента t_набл=4,2, а критическая точка критерия t_кр=2,3 при … r=0,65 – это означает, что линейная корреляционная связь между признаками

Значимая

• Факторы в дисперсионном анализе обозначаются

A, B, C …

• Что называется дисперсионным анализом

статистический метод, позволяющий оценить влияние одного или нескольких факторов на результативный…

• Найти выборочное среднее и выборочную дисперсию по данному распределению

4,2 и 0,8

• Установите соответствие между названием статистического критерия и его типом

Критерий знаков: непараметрический

Критерий Фишера: параметрический

• В случае, если при проверке гипотезы о равенстве дисперсий выяснилось, что наблюдаемое значение критерий выше критического, можно сделать вывод

различие генеральных дисперсий значимо

• К параметрическим критериям проверки статистических гипотез относится

Критерий Стьюдента

• Наблюдаемое значение критерия Фишера равно

отношению большей дисперсии к меньшей

• Требование, которое не предъявляется к выборке для применения параметрических критериев статистических гипотез

экспоненциальный закон распределения

• Наблюдаемое значение критерия определяется следующим образом

по формуле

• Критерий, с помощью которого не исследуют соответствие закона распределения выборочных данных некоторому известному закону распределения

Стьюдента

• Дана двумерная выборка, коэффициент которой равен r=0.75

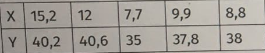
Если все значения переменных X и Y увеличить в 2 раза, то коэффициент корреляции станет равен

0,75

• Достоинства регрессионного анализа

устанавливает форму связи между признаками

позволяет предсказать значение у, если х изменится хотя бы на 1

• Гипотеза Н₀ для проверки значимости выборочного коэффициента линейной корреляции

r_ген = 0

• На рисунке приведено корреляционное поле точек, чему примерно равен коэффициент корреляции r

0

• Дана двумерная выборка, коэффициент корреляции которой равен r=-0.85

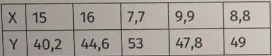
-0.85

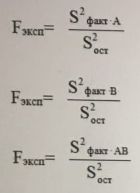
• Укажите формулы расчета экспериментального значения F-критериев при анализе двухфакторных комплексов

-

• Для оценки достоверности действия фактора на результативный признак применяется критерий

Фишера

• На чем основан дисперсионный анализ

на разложении общей дисперсии статистического комплекса на составляющие компоненты

• Найти выборочное среднее и выборочную дисперсию по данному распределению

3.3 и 2.2

• Установите соответствие между названием статистического критерия и его типом

Критерий Пирсона: согласия

Критерий Стьюдента: параметрический

• Справедливость нулевой гипотезы проверяется

сравнением наблюдаемого значений критерия и критического

• Критическое значения критерия определяется следующим образом

по таблице

• Требование, которое не предъявляется к выборке для применения параметрических критериев проверки статистических гипотез

экспоненциальный закон распределения

• К параметрическим критериям проверки статистических гипотез не относится

Критерий знаков

• К параметрическим критериям проверки статистических гипотез относится

Критерий Стьюдента

• Наблюдаемое значение критерия Фишера равно

отношению большей дисперсии к меньшей

• Критическое значения критерия зависит от

числа степеней свободы и уровня значимости

• Параметрический статистический критерий – это функция, зависящая от

параметров данной совокупности

• В случае, если при проверке гипотезы о равенстве дисперсий выяснилось, что наблюдаемое значение критерия выше критического, можно сделать вывод

различие генеральных дисперсий значимо

• Число степеней свободы для определения критического значения критерия Стьюдента в задаче проверки гипотезы о равенстве средних значений в выборках определяется по формуле Выберите один ответ

f=n1+n2-2

• На рисунке приведены две корреляционные зависимости от х. Очевидно, что в случае А

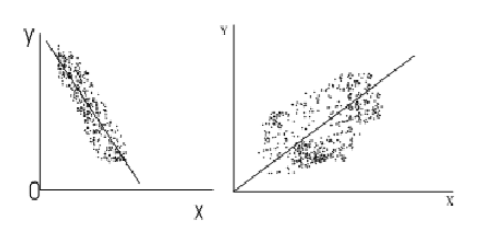
Связь обратная, а в случае Б связь прямая

• Коэффициент корреляции r=0. Это говорит о том, что

Линейная корреляционная зависимость отсутствует

• Имеется двумерная выборка объема 9 . Коэффициент корреляции между признаками Х и Y равен r=0,7; наблюдаемое значение T-критерия Стьюдента Тнабл=2,0, а критическая точка Tкр=2,36 . Это означает, что линейная связь между признаками Х и Y:

Отсутствует

• Если наблюдаемое значение t-критерия Стьюдента t_набл =4,5, а критическое t_кр =2,3 при α ≤ 0, 05, r=-0,95 - это означает , что линейная корреляционная связь между признаками:

Очень сильная

Заметная

• Дисперсионный анализ применяют

При изучении влияния факторов на результативный признак

• Виды дисперсионного анализа различают по количеству

Изучаемых факторов

• Найти выборочное среднее и выборочную дисперсию по данному распределению:

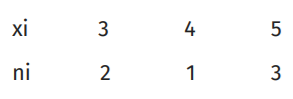
4.2 и 0.8

• Установите соответствие между названием статистического критерия и его типом

Критерий Пирсона: согласия

Критерий Стьюдента: параметрический

• К параметрическим критериям проверки статистических гипотез относится

Критерий Стьюдента

• Гипотеза H0, заключающаяся в том, что сравниваемые генеральные параметры равны и различия, наблюдаемые между выборками случайны, называется

Основная

• Гипотеза H1, противоречащая H0 и заключающаяся в том, что сравниваемые генеральные параметры различаются, называется

Альтернативная

• Критическое значение критерия зависит от

Числа степеней свободы и уровня значимости

• Число, которое может стать уровнем значимости

0,01

• Число, которое не может стать уровнем значимости

0,5

• К параметрическим критериям проверки статистических гипотез не относится

Критерий знаков

• Параметрический статистический критерий - это функция, зависящая от

Параметров данной совокупности

• Уровень значимости принимается равным

Малому числу (0,001; 0,01, 0,05)

• Гипотеза для проверки значимости выборочного коэффициента линейной корреляции:

r_ген ≠ 0

• Если наблюдаемое значение Т-критерия Стьюдента Тнабл=4,2 (a,f), а критическая Ткр =2.3 при a≤0.05, то можно сделать вывод , что линейная связь между признаками X и Y:

Имеется

• Если наблюдаемое значение t-критерия Стьюдента t_набл =4,2, а критическая точка критерия t _кр=2,3 при α ≤ 0, 05, r=0,65 - это означает , что линейная корреляционная связь между признаками:

Значимая

• Если наблюдаемое значение t-критерия Стьюдента t_набл=4,5, а критическое t_кр =2,3 при α ≤ 0, 05, r=-0,95 - это означает , что линейная корреляционная связь между признаками:

Обратная

• Дисперсионный анализ применяют:

При изучении влияния факторов на результативный признак

• Найти выборочное среднее и выборочную дисперсию по данному распределению:

3,3 и 2,2

• Установите соответствие между названием статистического критерия и его типом. Критерий Фишера параметрический

Критерий знаков непараметрический

• Наблюдаемое значение критерия Фишера всегда

Больше либо равно единице

• Правило, позволяющее основываясь только на выборке принять или отвергнуть нулевую гипотезу, называется

Статистический критерий

• Наблюдаемое значение критерия определяется следующим образом

По формуле

• Уровень значимости выбирается следующим образом

Задается исследователем

• В случае, если при проверке гипотезы о равенстве средних выяснилось, что наблюдаемое значение критерия ниже критического, можно сделать вывод

Различие генеральных средних незначимо

• Справедливость нулевой гипотезы проверяется

Сравнением наблюдаемого значения критерия и критического

• Вероятность ошибки отвергнуть нулевую гипотезу, если в действительности она верна, называется

уровень значимости

• Для проверки гипотез о равенстве дисперсий из параметрических критериев используют критерий

Фишера

• При использовании параметрических критериев нулевая гипотеза принимается при

Кнабл меньше Ккрит

• Коэффициент корреляции r=0. Это говорит о том, что

Линейная корреляционная зависимость отсутствует

• Если все значения переменной в двумерной выборке увеличится в 2 раза, то коэффициент корреляции:

Не изменится

• Причина, вызывающая изменения величины результативного признака.

Контролируемые и неконтролируемые факторы

• Дисперсионный анализ применяют:

При изучении влияния факторов на результативный признак.

• Найти выборочное среднее и выборочную дисперсию по данному распределению:

4.3 и 3.4

• Гипотеза H0, заключающаяся в том, что сравниваемые генеральные параметры равны и различия, наблюдаемые между выборками случайны, называется

Основная

• Уровень значимости выбирается следующим образом:

Задается исследователем

• Для проверки гипотез о равенстве средних из параметрических критериев используют критерий

Стьюдента

• Один из критериев, при помощи которого проверяют соответствие закона распределения выборочных данных некоторому известному закону распределения

Пирсона

• Критическое значение критерия зависит от

числа степеней свободы и уровня значимости

• Любое высказывание о генеральной совокупности, проверяемое по выборке, называется

статистическая гипотеза

• К параметрическим критериям проверки статистических гипотез относится

Критерий Стьюдента

• Число степеней свободы для определения критического значения критерия Стьюдента в задаче проверки гипотезы о равенстве средних значений в выборках определяется по формуле

f=n1+n2-2

• Гипотеза Н₀ для проверки значимости выборочного коэффициента линейной корреляции:

R_ген = 0

• Достоинства регрессионного анализа:

Устанавливает форму связи между признаками

Позволяет предсказать значение y, если х изменится хотя бы на 1 d.

Выражает корреляционную зависимость в виде функционального соотношения

• Найти выборочное среднее и выборочную дисперсию по данному распределению:

1.7 и 0.6

• Число степеней свободы для определения критического значения критерия Пирсона в задаче проверки гипотезы о соответствии распределения заданному закону

f=k-3

• Критическое значение критерия определяется следующим образом

По таблице

• Если объем двумерной выборки меньше 100, то формула ошибки m коэффициента корреляции имеет вид

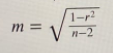
• Гипотеза H1, противоречащая H0 и заключающаяся в том, что сравниваемые генеральные параметры различаются, называется

Альтернативная

• На рисунке приведены два корреляционных поля точек. Очевидно, что в случае А

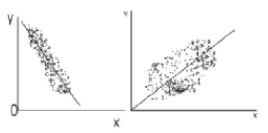
Коэффициент корреляции близок к -1, а в случае б стремится к 0

• Найти выборочное среднее и выборочную дисперсию по данному распределению

xi 3 5 2

ni 3 2 5

2.9 и 1.3

• Критическое значение критерия не зависит от

Математического ожидания

• Если коэффициент корреляции между признаками X и Y равен 0.5, то что можно сказать о коэффициенте корреляции, характеризующим связь между признаками Y и X?

Равен 0.5

• В случае, если при проверке гипотезы о соответствии закона распределения H3P, наблюдаемое значение критерия меньше критического, можно сделать вывод

Различие генеральных средних незначимо

• Найти выборочное среднее и выборочную дисперсию по данному распределению: xi 2 3 5 ni 5 3 2

2.9 и 1

• Выборочный коэффициент корреляции r_B является оценкой генерального коэффициента корреляции r_r, тем более точной, чем объем выборки

Больше

• О линейной регрессии говорят, если график регрессии изображается

Прямой линией

• Нулевую гипотезу н₀ считают согласующейся с результатами наблюдений, если

F_эксп < F_кр (4.5a, f₁, f₂ )