ЛР3

­­Министерство цифрового развития, связи и массовых коммуникаций РФ ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

«МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ»

Кафедра «Системное программирование»­­

Лабораторная работа №3

по дисциплине «Интеллектуальные системы»

Тема: «Изучение способов представления и исследования сетей Петри»

Вариант №16

Выполнил: студент группы

Проверил:

Кулагин В. П.

Москва, 2025 г.

Оглавление

Введение 3

Поставленная задача 4

ХОД РАБОТЫ 6

Введение

Данная работа представляет собой возможность изучить работу с сетями Петри. При выполнении данной работы будут приобретены необходимые навыки для выполнения различных задач, в которых используются данные технологии.

Поставленная задача

Цель работы:

Изучение методов синтеза параллельных многопроцессорных вычислительных структур с использованием аппарата сетей Петри и тензорной методологии.

Пусть имеется некоторая исходная СП-модель, выполняющая функции исследуемого объекта. Кроме данной СП-модели, очевидно, существуют и другие модели, выполняющие аналогичные функции, но отличающиеся от исходной характеристиками.

Задача состоит в том, чтобы найти эти модели, а также рассмотреть методы, позволяющие их синтезировать.

Постановка задачи:

1. Получить вариант задания у преподавателя на построение СП-модели N.

2. Построить структурную схему многопроцессорной системы для заданного варианта. Определиться с потоком входных (матрицы А и В) и генерируемых данных (матрица С).

3. Построить структуру процессорного элемента.

4. Построить таблицу, демонстрирующую потактовую работу построенной многопроцессорной структуры.

5. Построить СП-модель, описывающую работу построенной многопроцессорной системы.

6. Убедиться в корректности работы СП-модели путем сравнения с таблицей потактовой работы.

7. Выполнить цикл работ по анализу базовой СП-модели N1, включающих:

   1. Декомпозицию исходной структуры на линейные и линейно-циклические фрагменты;

   2. Построение примитивной системы;

   3. Построение тензора преобразования.

8. Выполнить операцию синтеза исходной СП-модели N1.

9. Построить программу синтеза заданной СП-модели (Nзд).

10. Построить матричное описание СП-модели по полученной программе синтеза в системе координат примитивной системы.

11. Выразить построенную СП-модель в исходной системе координат (с помощью тензора преобразования).

12. Удалить эквивалентные вершины и провести моделирование построенной СП-модели с помощью программного комплекса GPTN.

13. Определить числовые характеристики построенной СП-модели по параметрам, согласованным с преподавателем.

ХОД РАБОТЫ

1. Условие варианта задачи:

Проекция многопроцессорной структуры по оси X-Y 45 градусов.

2. Структурная схема многопроцессорной системы для заданного варианта (рис. 1):

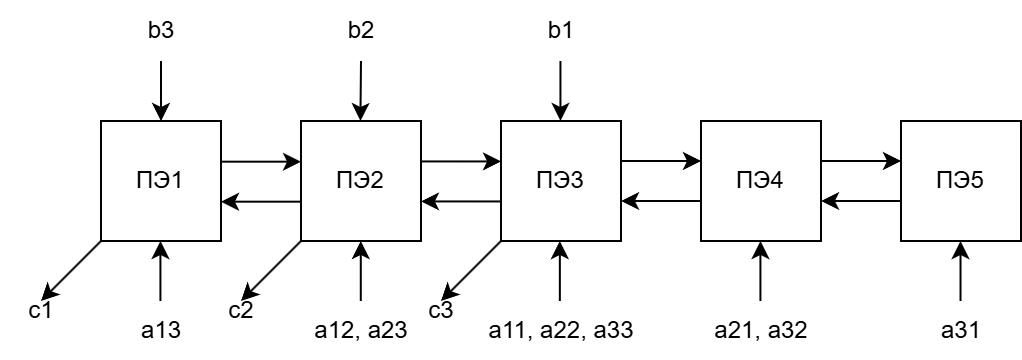
Рисунок 1 – Структурная схема многопроцессорной системы

3. Структура процессорных элементов (рис. 2-6)

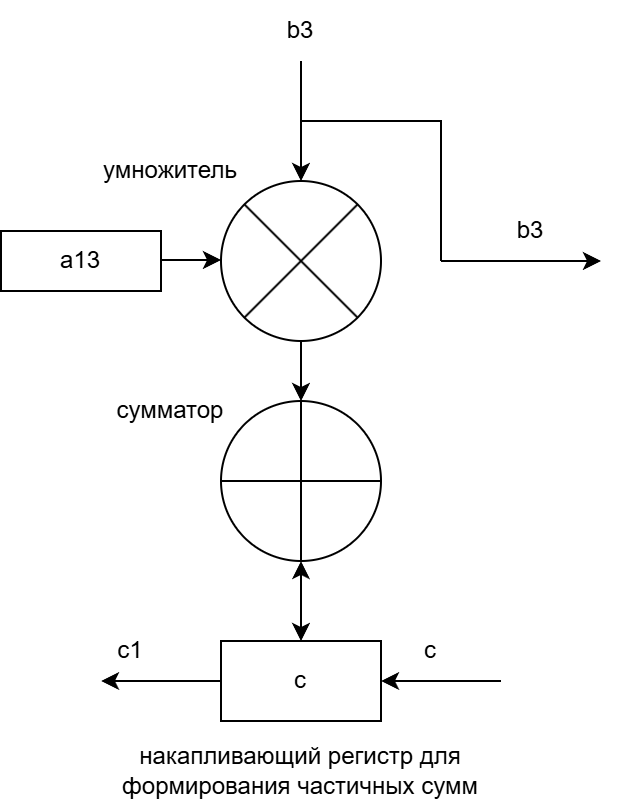
Рисунок 2 – Структура ПЭ1

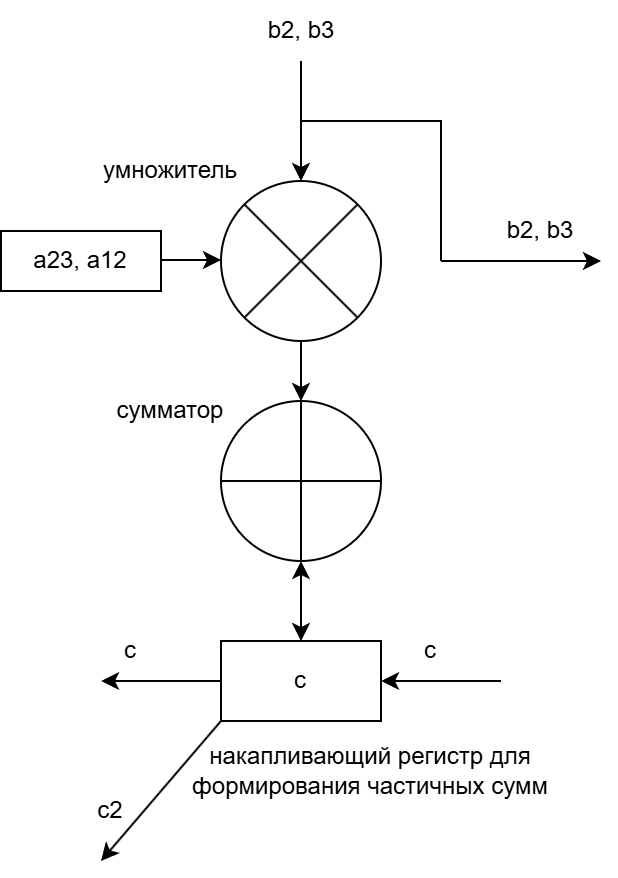
Рисунок 3 – Структура ПЭ2

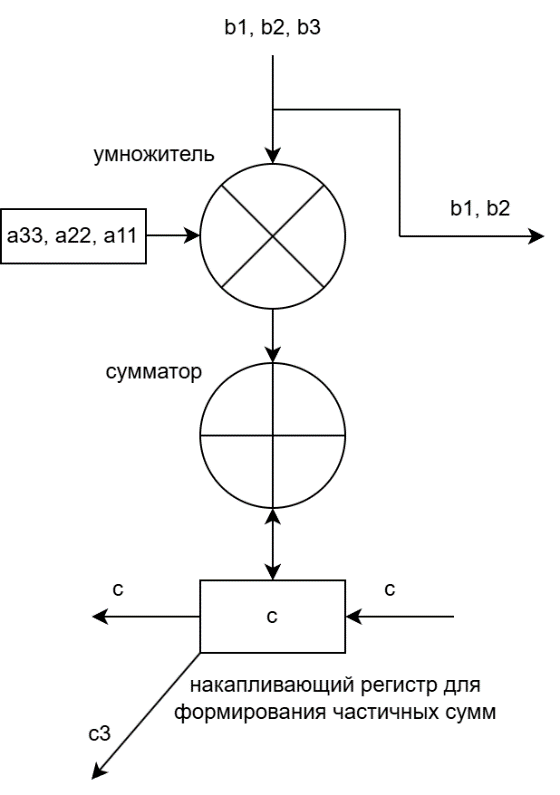
Рисунок 4 – Структура ПЭ3

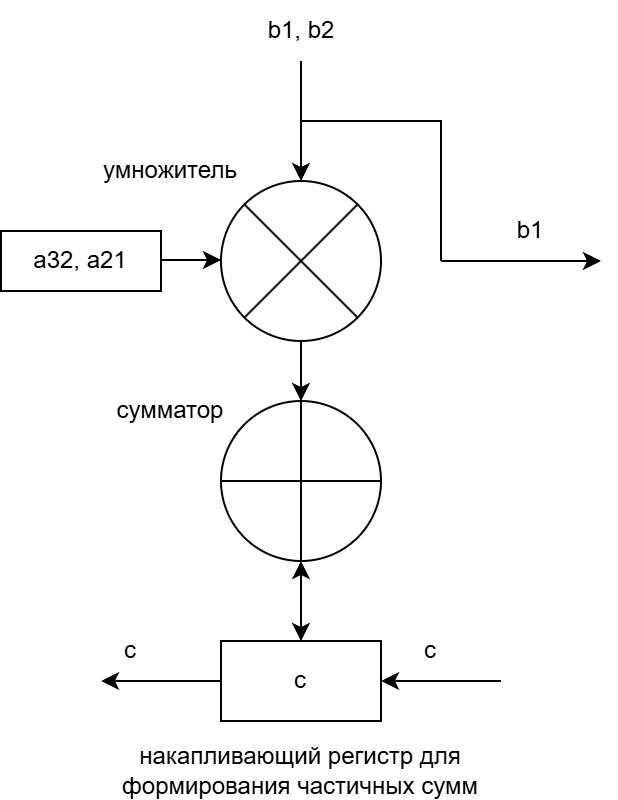
Рисунок 5 – Структура ПЭ4

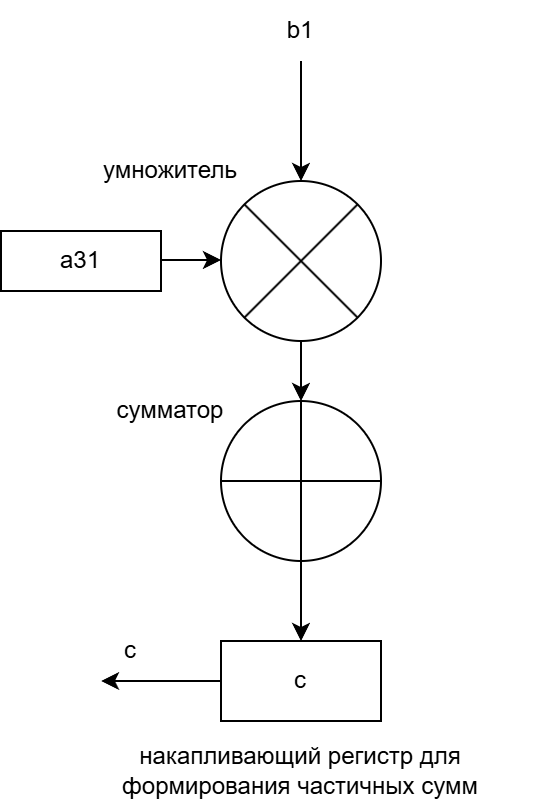
Рисунок 6 – Структура ПЭ5

4. Построим потактовую таблицу (табл. 1):

Таблица 1 – Потактовая таблица

	ПЭ1	ПЭ2	ПЭ3	ПЭ4	ПЭ5
1			b1a11
2		b1a11 + b2a12		b1a21
3	b1a11 + b2a12 + b3a13		b1a21 + b2a22		b1a31
4		b1a21 + b2a22 + b3a23		b1a31 + b2a32
5			b1a31 + b2a32 + b3a33

5. Построим СП-модель (рис. 7)

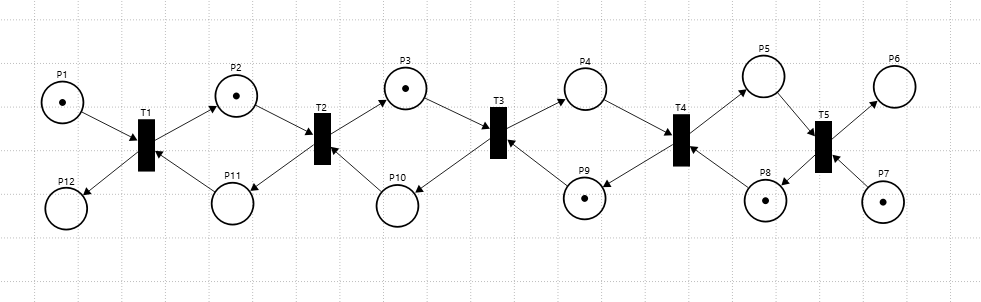
Рисунок 7 – СП модель

6. Убедимся в корректности работы СП-модели путем сравнения с таблицей потактовой работы (рис. 8).

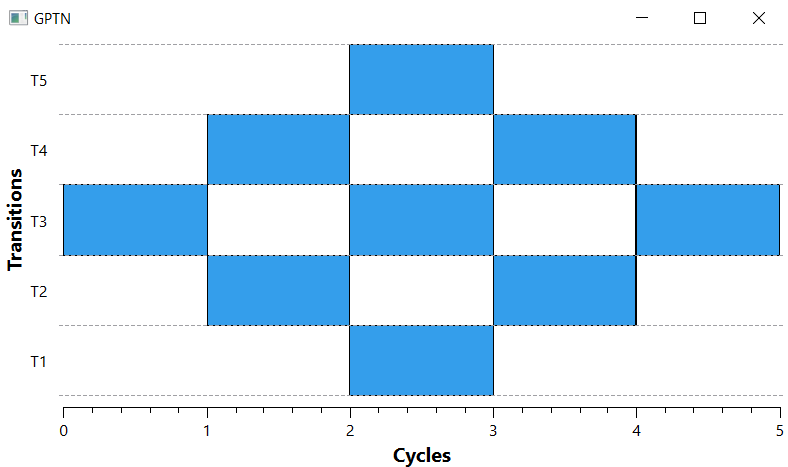
Рисунок 8 – Работа построенной СП-модели

Можем убедиться, что количество тактов соответствует построенной таблице

7. По структурной схеме построим соответствующей ей СП модель, рисунок 9

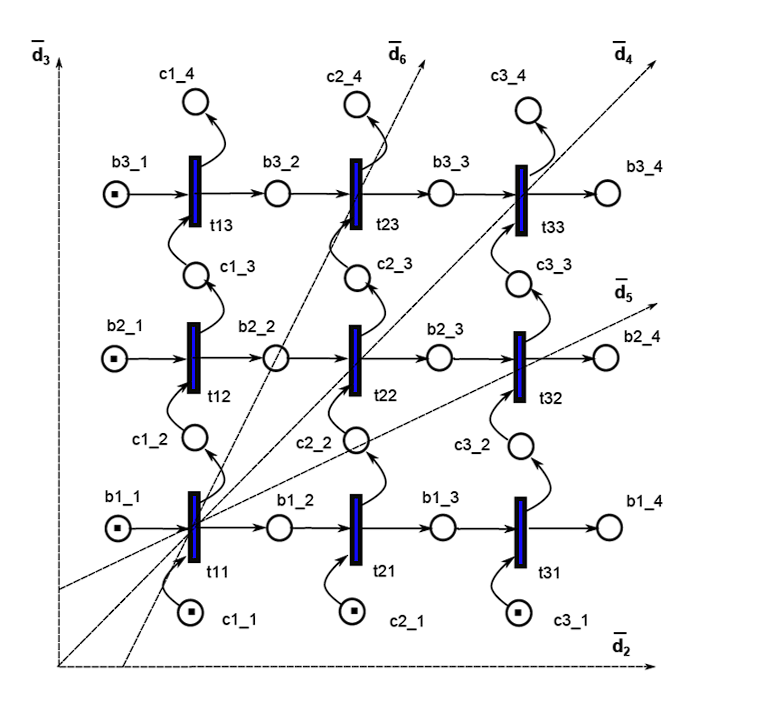
Рисунок 9 – Базовая СП модель

После выполним анализ базовой СП модели:

1. Произведем декомпозицию исходной структуры на линейные и линейно-циклические фрагменты, рисунок 10:

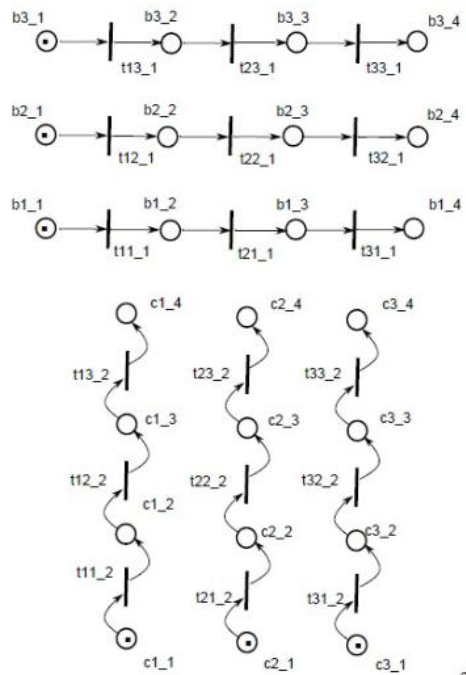
Рисунок 10 – Декомпозиция базовой СП модели

2. Для построения примитивной системы следует ввести эквивалентные позиции, чтобы размерности матриц, описывающие систему с ЛБФ и примитивную систему, совпадали, рисунок 11.

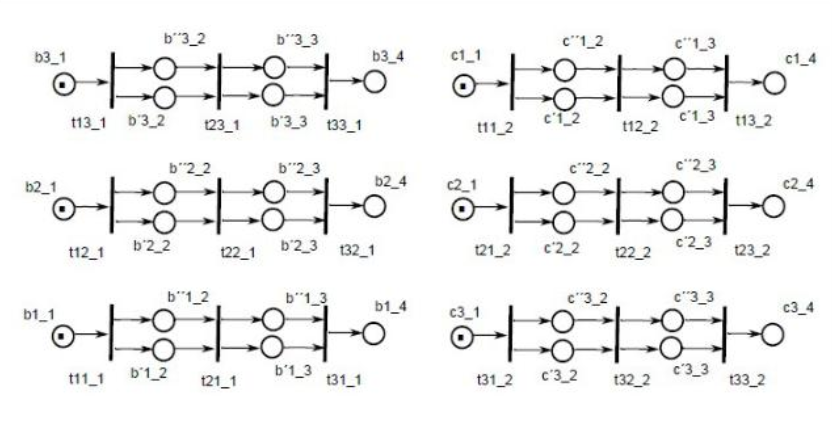
Рисунок 11 – Система ЛБФ с эквивалентными позициями

Следующим шагом является разделение переходов, деление головной и хвостовой позиций. Таким образом, получаем примитивную СП-модель, рисунок 12.

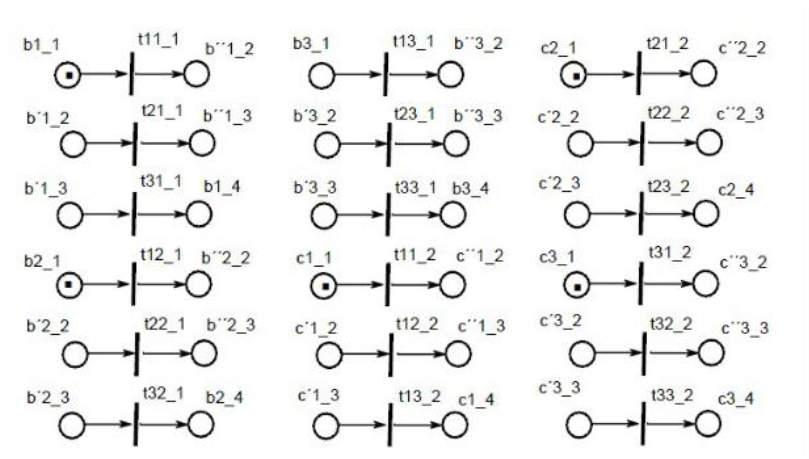
Рисунок 12 – Примитивная система

3. Тензор преобразования можно получить исходя из формулы, изображенная на рисунке 13.

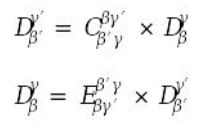
Рисунок 13 – Формула тензора преобразования

Где:

– это матрица инцидентности примитивной системы, рисунок 14;

– это матрица инцидентности системы ЛБФ, рисунок 15.

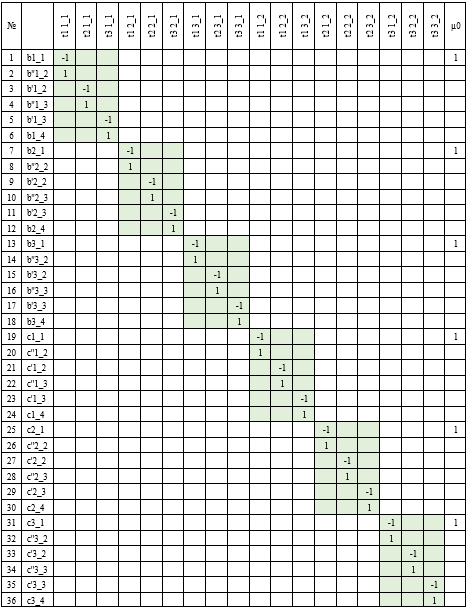
Рисунок 14 – Матрица инцидентности примитивной системы

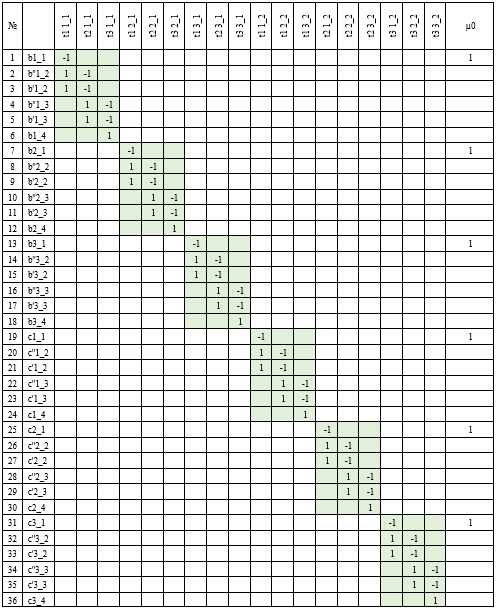
Рисунок 15 – Матрица инцидентности системы ЛБФ

На основании формулы находим тензор преобразования, рисунок 16.

­

Рисунок 16 – Тензор преобразования

8. Программа синтеза исходной СП-модели.

t11 = t11_1 + t11_2

t12 = t12_1 + t12_2

t13 = t13_1 + t13_2

t21 = t21_1 + t21_2

t22 = t22_1 + t22_2

t23 = t23_1 + t23_2

t31 = t31_1 + t31_2

t32 = t32_1 + t32_2

t33 = t33_1 + t33_2

Последовательность V, соответствующая данной программе, представлена на рисунке 17. Ввиду того что при синтезе СП-модели N1 объединения позиций не происходит (разряды части VP равны нулю), последовательность представлена только частью 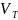. Рассмотрим процедуру синтеза данной СП-модели с использованием тензорного подхода.

Рисунок 17 – Программа синтеза исходной СП-модели N1 (часть )

На рисунке 18 представлена матрица инцидентности D1 исходной СП-модели N1 (с учетом исключения эквивалентных переходов), выраженная в системе координат примитивной системы. Можно убедиться, что полученная матрица инцидентности D1′ в точности описывает СП.

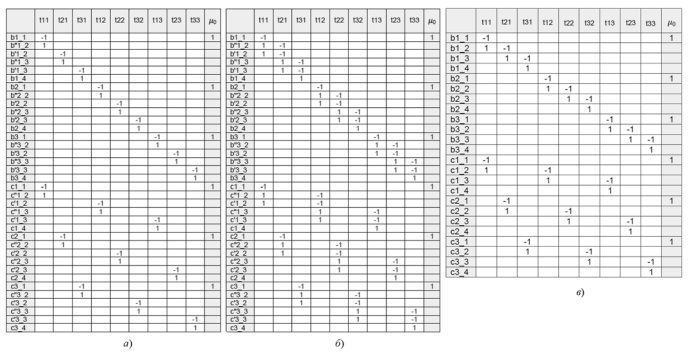
Рисунок 18 – Матрицы инцидентности исходной СП-модели N1:

а — матрица D1; б — матрица D1′; в — матрица D1′ после удаления эквивалентных вершин

9. На рисунке 19 показана СП-модель, которую необходимо синтезировать.

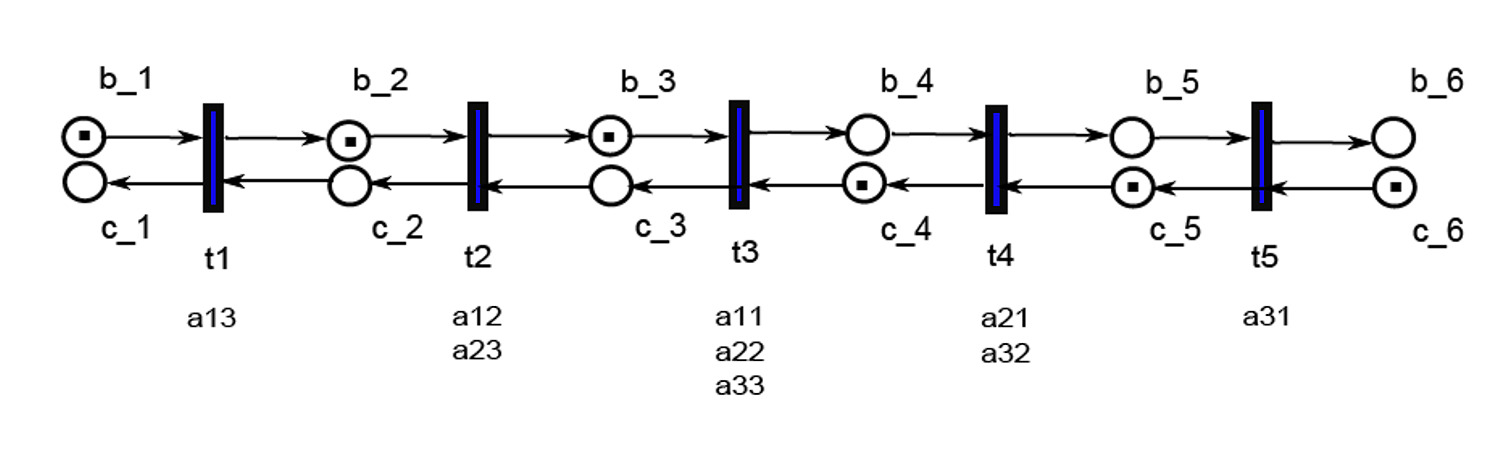
Рисунок 19 – СП, которую необходимо синтезировать

Далее построим программу синтеза для заданной по варианту СП-модели:

b_1 = b3_1

b_2 = b2_1+ b’3_2 + b”3_2

b_3 = b1_1 + b’2_2 + b’3_3 + b”2_2 + b”3_3

b_4 = b’1_2 + b’2_3 + b”1_2 + b”2_3 + b3_4

b_5 = b2_4 + b’1_3 + b”1_3

b_6 = b1_4

c_1 = c1_4

c_2 = c’1_3 + c”1_3 + c2_4

c_3 = с’1_2 + c”1_2 + c’2_3 + c”2_3 + c3_4

c_4 = c1_1 + c’2_2 + c”2_2 + c’3_3 + c”3_3

c_5 = c2_1 + c’3_2 + c”3_2

c_6 = c3_1

t1 = t13

t2 = t12 + t23

t3 = t11 + t22 + t33

t4 = t21 + t32

t5 = t31

На рисунке 20 представлена таблица объединения позиций согласно программе синтеза.

Рисунок 20 – Таблица объединения позиций и переходов согласно программе синтеза

10. На рисунке 21 представлена таблица с матрицей инцидентности примитивной системы N4 в координатах примитивной системы после программы синтеза.

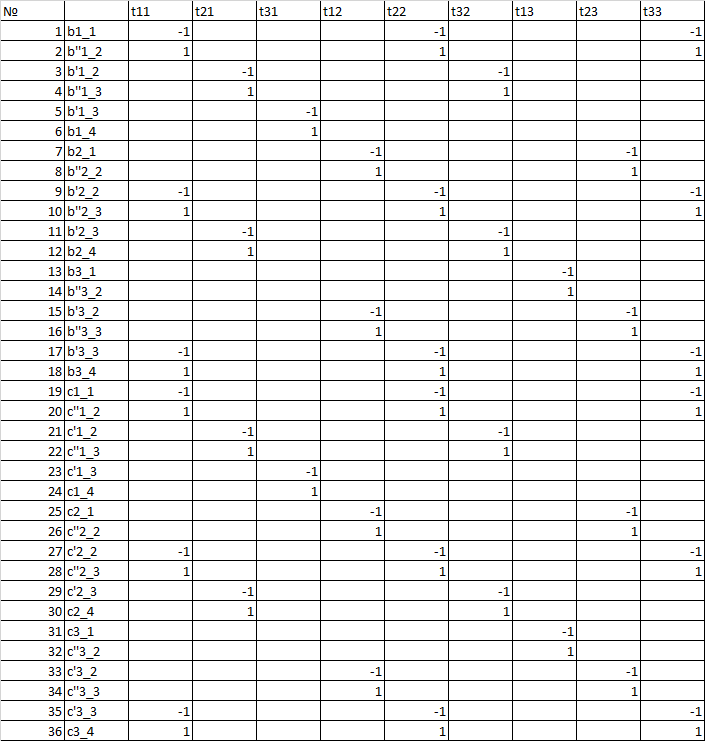
Рисунок 21 – Матрица инцидентности примитивной системы N4 в координатах примитивной системы после программы синтеза

11. На рисунке 22 представлена матрица N4 после умножения тензора преобразования на матрицу инццидентности примитивной системы на рисунке 16.

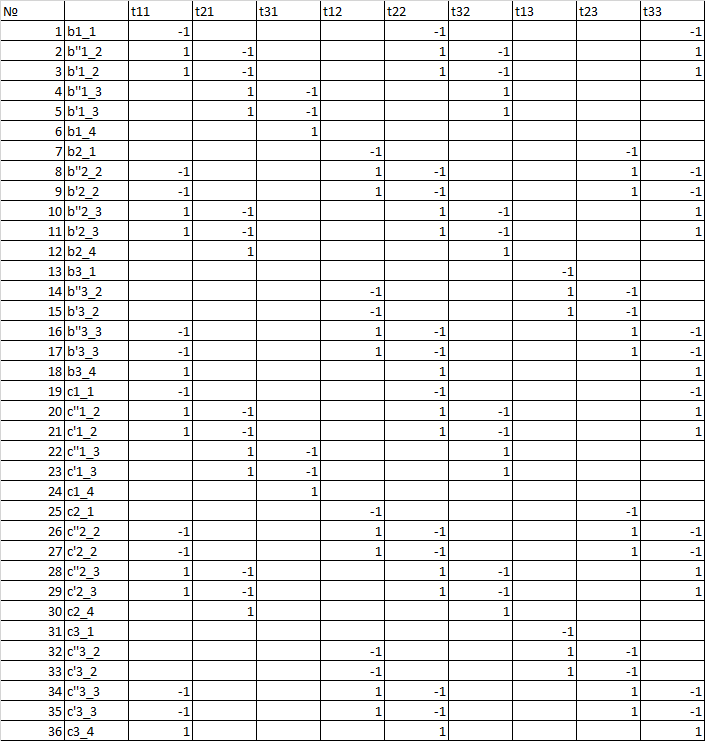
Рисунок 22 – Матрица N4 после умножения тензора преобразования на матрицу инццидентности примитивной системы

12. Удалим эквивалентные вершины и позиции, рисунок 23.

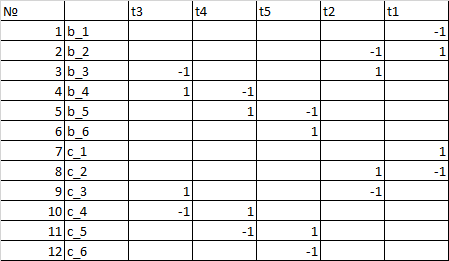
Рисунок 23 – Удаление эквивалентных вершин

Проведем моделирование модели на рисунке 24. ДДР изображено на рисунке 25.

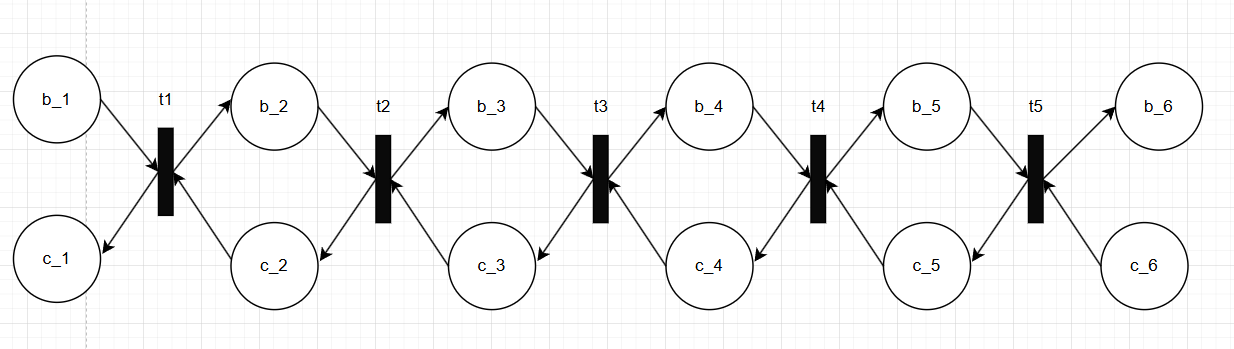
Рисунок 24 – Модель СП в на основе синтеза

Рисунок 25 – Дерево достижимых разметок

Такты данной СП изображены на рисунках 26-30.

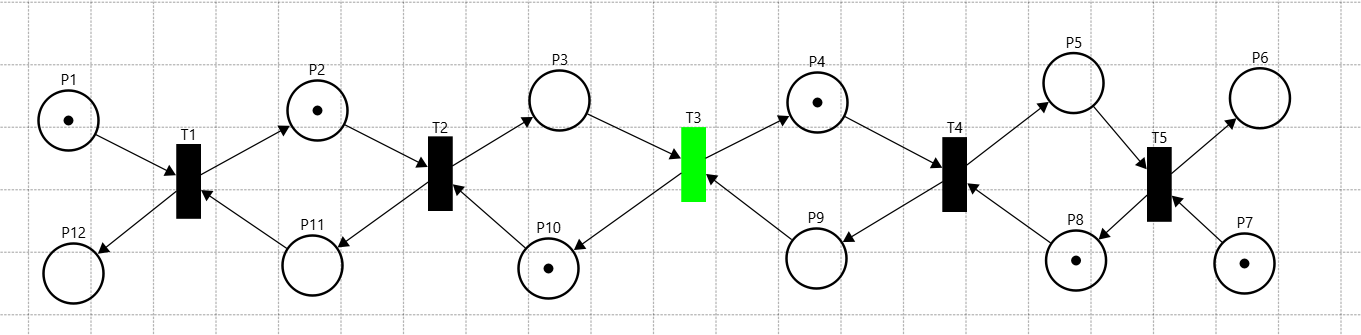
Рисунок 26 – 1-ый такт СП

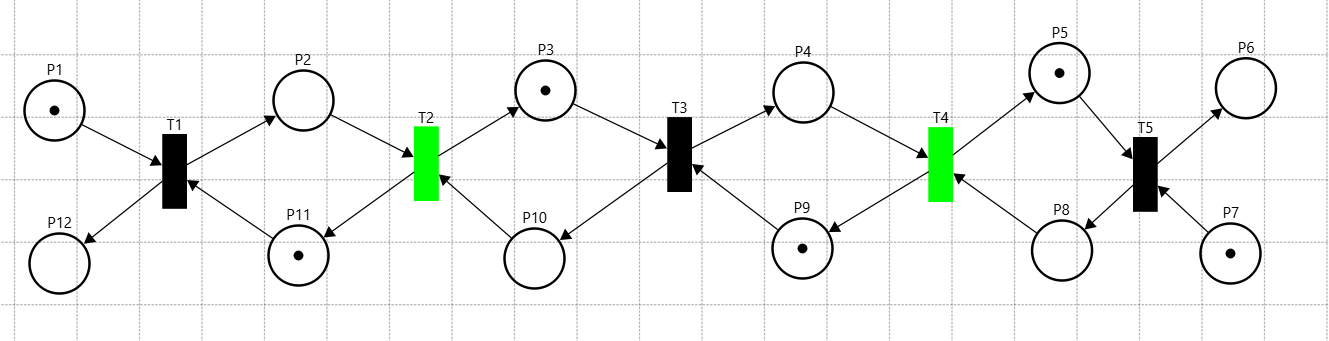
Рисунок 27 – 2-ой такт СП

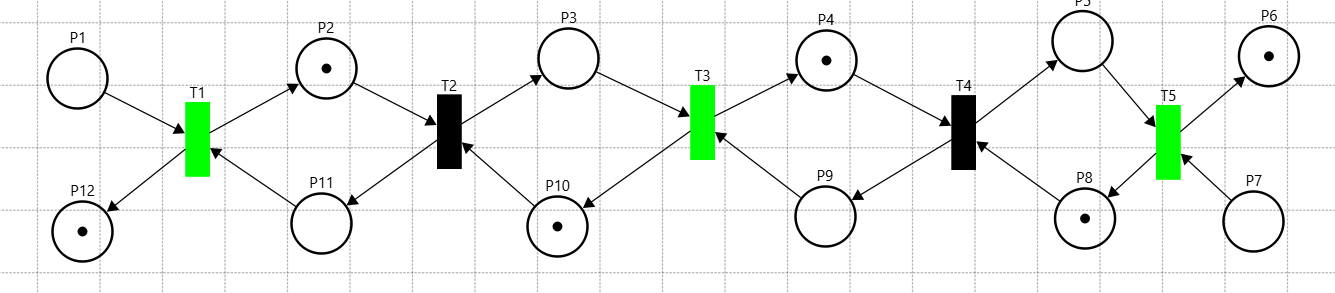
Рисунок 28 – 3-ий такт СП

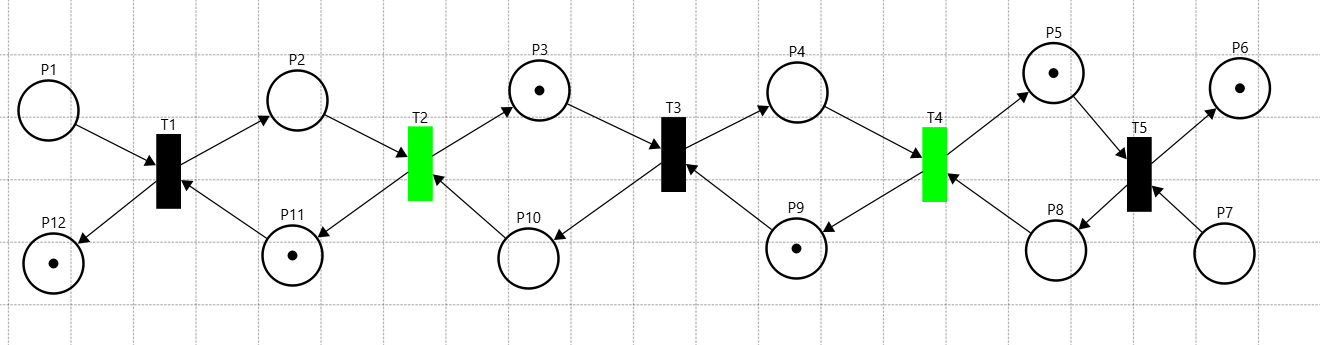
Рисунок 29 – 4-ый такт СП

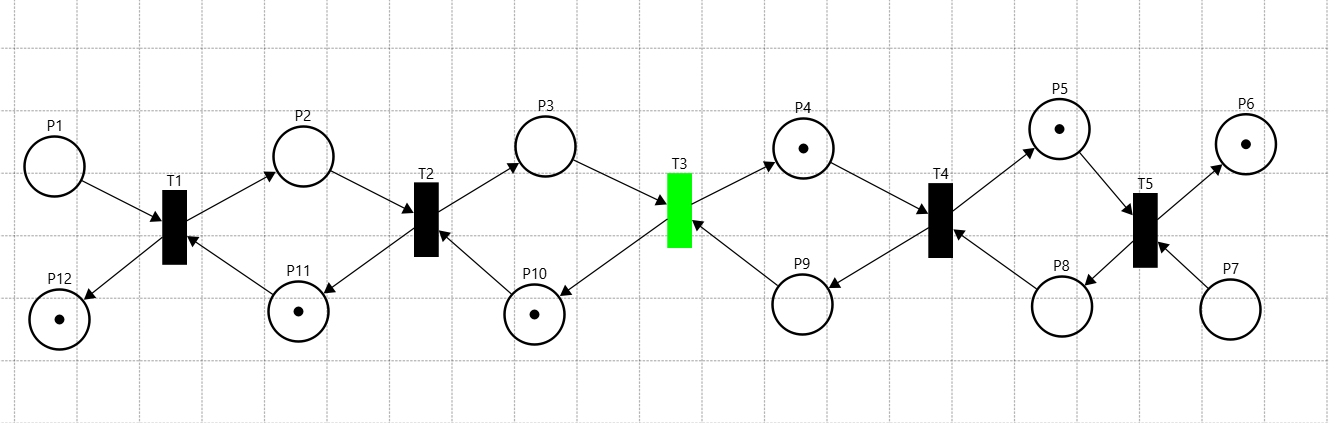
Рисунок 30 – 5-ый такт СП

На рисунке 31 изображена потактовая работа ПЭ, сделанная с помощью программного комплекса GPTN.

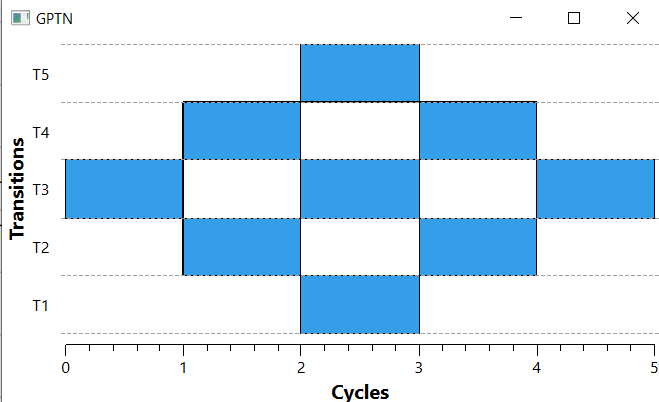
Рисунок 31 – Потактовая работа ПЭ

13. Определим числовые характеристики построенной СП модели:

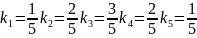
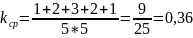
На таблице 2 показана сравнительная оценка синтезированных СП-моделей, где N₄ – разбираемая нами модель.

Таблица 2 – Сравнительная оценка синтезированных СП-моделей

№	Идентификатор СП модели	Число ПЭ	Число тактов	Коэффициент использования ПЭ (ki)	Средний коэффициент использования ПЭ (kср)
1	N1	9	5	1/5	0,2
2	N2	3	5	3/5	0,6
3	N3	3	5	3/5	0,6
5	N4	5	5	Величина переменная	0,36
6	N5	7	5	Величина переменная	0,26
7	N6	7	5	Величина переменная	0,26
8	N7	9	5	1/5	0,2
9	N0	1	9	1	1

На рисунке 32 показана зависимость среднего коэффициента использования ПЭ синтезированных структур от числа ПЭ.

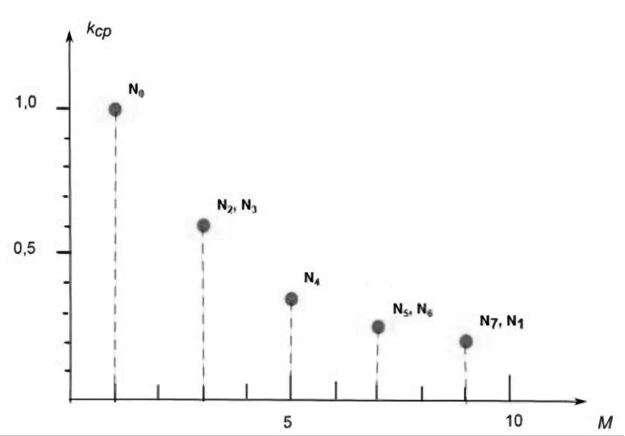
Рисунок 32 – Зависимость среднего коэффициента использования ПЭ синтезированных структур от числа ПЭ

ВЫВОД

По итогам работы была изучена работа синтеза параллельных многопроцессорных вычислительных структур. Были приобретены необходимые навыки для выполнения различных задач, в которых используются данные технологии.