Министерство цифрового развития, связи и массовых коммуникаций РФ ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

«МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ»

Кафедра «Системное программирование»

Лабораторная работа №2

по дисциплине «Интеллектуальные системы»

Тема: «Изучение способов представления и исследования сетей Петри»

Вариант №16

Выполнил: студент группы

Проверил:

Кулагин В. П.

Москва, 2025 г.

Оглавление

Введение 3

Поставленная задача 4

ХОД РАБОТЫ 6

Введение

Данная работа представляет собой возможность изучить работу с сетями Петри. При выполнении данной работы будут приобретены необходимые навыки для выполнения различных задач, в которых используются данные технологии.

Поставленная задача

Цель работы:

Изучение методов использования иерархических сетей Петри при анализе многоуровневых вычислительных структур с распределенными ресурсами.

Постановка задачи:

1. Построить структурную схему для заданного варианта ВС.

2. Построить модель ВС в терминах иерархической сети Петри (СП). Дать интерпретацию вершин СП-модели в терминах блоков и функций ВС.

3. Задать на первом этапе исследования СП-модели низкую интенсивность входных данных: новые данные для обработки вводятся только после вывода уже обработанных данных из системы.

4. Описать построенную модель с помощью матричных методов, а также с помощью алгебраических выражений. Использовать для уменьшения размерностей возможности иерархических СП. Провести анализ полученной СП-модели.

5. Провести анализ построенной СП-модели с использованием программного комплекса. Убедиться в корректном функционировании СП (отсутствие тупиковых ситуаций и бесконечно размеченных позиций).

6. Приступить ко второму этапу анализа СП-модели - задать интенсивный режим поступления входных данных. В этом случае ввод данных в систему разрешается после отправки предварительно введенных данных на обработку в процессорные элементы.

7. Провести анализ модифицированной СП-модели с использованием программного комплекса. На основе исследования сделать выводы о корректности модели, предложить варианты устранения недостатков в случае их обнаружения.

8. Убедиться в повышении производительности модифицированной системы.

Ход работы

Условие варианта задачи:

Даны вычислительные структуры BC1 и ВС2, которые имеют соответственно параллельный (ПЭ1||ПЭ2) и последовательный (ПЭ1−ПЭ2) процессоры. Обработка данных в процессорах BC1 и ВС2 начинается одновременно. Канал ввода-вывода имеет один подканал и выполняет ввод и вывод данных в каждой вычислительной структуре.

1. Построить структурную схему для заданного варианта вс.

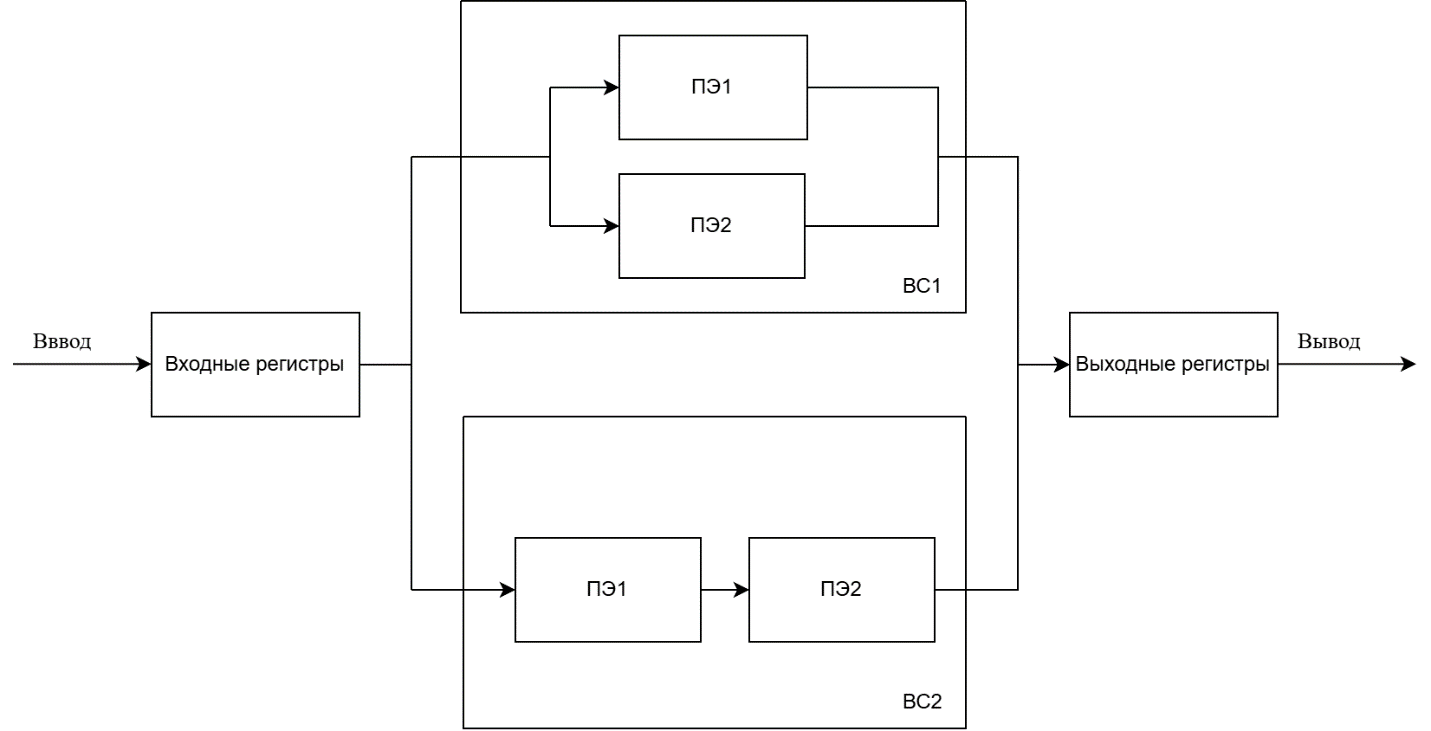
Рисунок 1 – Структурная схема для заданного варианта ВС

2. Построить модель вс в терминах иерархической сети Петри (сп). Дать интерпретацию вершин сп-модели в терминах блоков и функций вс.

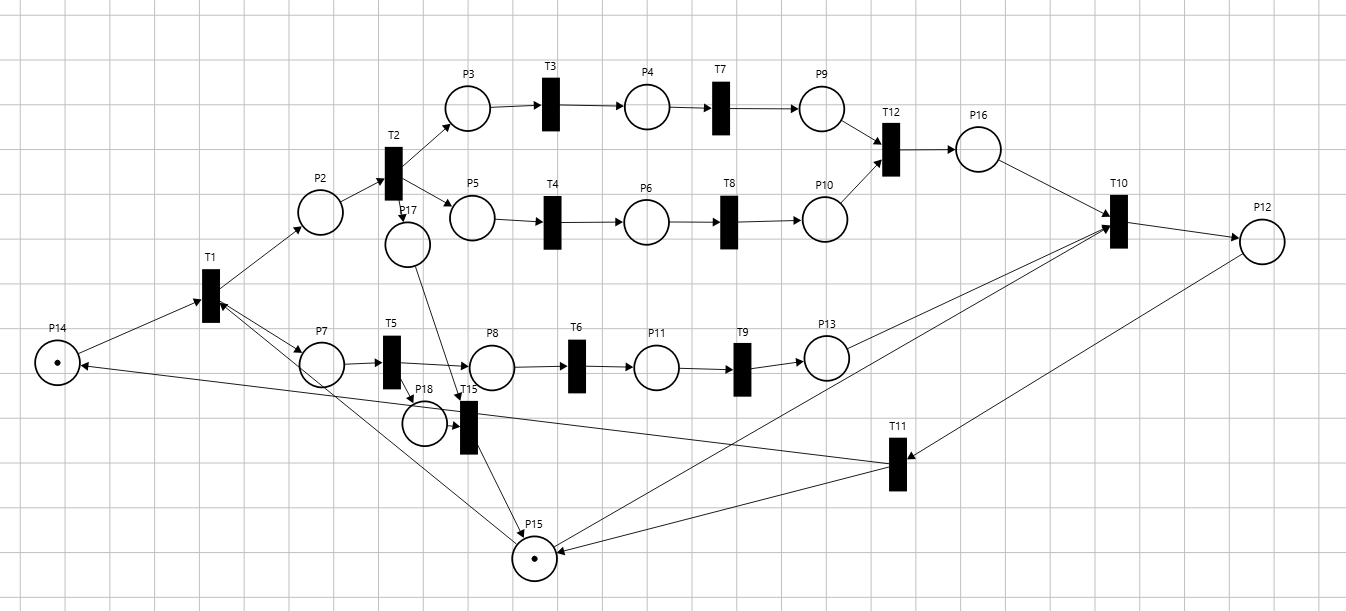
Рисунок 2 – модель ВС в терминах ИСП

Интерпретация данной сети:

T1 – начало ввода данных в ВС1 и ВС2

Для ВС1:

T2 – начало ввода данных в ПЭ1 и ПЭ2

T3 – обработка данных в ПЭ1

T7 – вывод обработанных данных из ПЭ1

P2 – данные введены и готовы для обработки в ВС1

P3 – данные введены и готовы для обработки в ПЭ1

P4 – идет обработка данных в ПЭ1

Аналогично для ПЭ2 (T4, T8, P5-P8)

Для ВС2:

T5 – Ввод данных в ПЭ1

T6 – Обработка данных в ПЭ1

Т9 – Обработка данных в ПЭ2

P7 – данные введены и готовы для обработки в ВС2

P8 – Данные введены для обработки в ПЭ1 и ПЭ2

P9 – Данные готовы к выводу

Подканал:

T1 – Данные вводятся в систему

P17 – Данные введены в ВС1

P18 – Данные введены в ВС2

Т15 – Освобождение подканала

T10 – Данные выводятся

P12 – Данные выведены

T11 – Освобождение подканала и ввод новых данных

Упростим сеть Петри, рисунок 3.

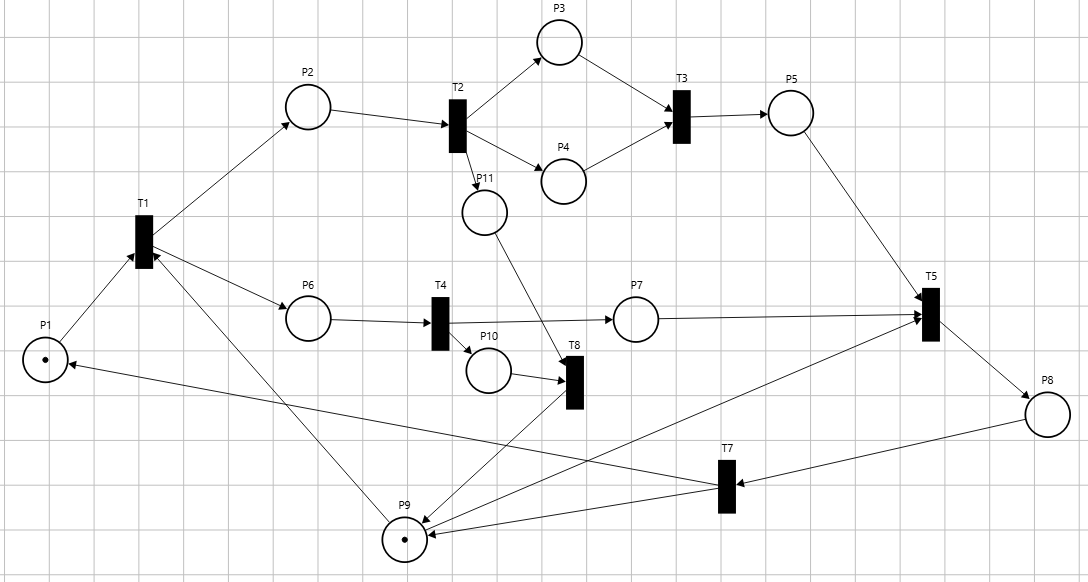
Рисунок 3 – Сокращённая сеть Петри

3. Найти матрицу инцидентности F, H^T, на основе которых вычислить матрицу C.

Найдем функцию инцидентности с помощью формулы F: PxT. В итоге получится матрица, изображенная в виде таблице на таблице 1.

Таблица 1 – Функция инцидентности F

F	T1	T8	T3	T5	T7	T2	T4
P1	1	0	0	0	0	0	0
P5	0	0	0	1	0	0	0
P8	0	0	0	0	1	0	0
P10	0	1	0	0	0	0	0
P4	0	0	1	0	0	0	0
P7	0	0	0	1	0	0	0
P11	0	1	0	0	0	0	0
P6	0	0	0	0	0	0	1
P3	0	0	1	0	0	0	0
P1	0	0	0	0	0	1	0
P10	1	0	0	1	0	0	0

Найдем функцию инцидентности с помощью формулы H: TxP. В итоге получится матрица, изображенная в виде таблице на таблице 2.

Таблица 2 – Функция инцидентности H^T

HT	T1	T8	T3	T5	T7	T2	T4
P1	0	0	0	0	1	0	0
P5	0	0	1	0	0	0	0
P8	0	0	0	1	0	0	0
P10	0	0	0	0	0	0	1
P4	0	0	0	0	0	1	0
P7	0	0	0	0	0	0	1
P11	0	0	0	0	0	1	0
P6	1	0	0	0	0	0	0
P3	0	0	0	0	0	1	0
P1	1	0	0	0	0	0	0
P10	0	1	0	0	1	0	0

На основе данных матриц вычислим матрицу C:

Таблица 3 – Матрица C

C	T1	T8	T3	T5	T7	T2	T4
P1	-1	0	0	0	1	0	0
P5	0	0	1	-1	0	0	0
P8	0	0	0	1	-1	0	0
P10	0	-1	0	0	0	0	1
P4	0	0	-1	0	0	1	0
P7	0	0	0	-1	0	0	1
P11	0	-1	0	0	0	1	0
P6	1	0	0	0	0	0	-1
P3	0	0	-1	0	0	1	0
P1	1	0	0	0	0	-1	0
P10	-1	1	0	-1	1	0	0

4. С помощью матричных методов можно показать, что если СП живая и ограниченная, то она должна быть последовательной и инвариантной. Данные свойства недостаточны для утверждения живости и ограниченности СП. Однако их полезно проверить исходя из матриц инцидентности, так как если одно из этих свойств не подтверждается, то можно заключить, что описываемая система содержит некоторые недоработки.

Рассмотрим матричные уравнения:

y*C=0, (1)

C*x=0, (2)

где у и x - векторы, размерность которых равна n и m соответственно.

Сначала рассмотрим уравнение (1), согласно которому получаем:

Рисунок 4 – Решение системы y*C методом Гаусса

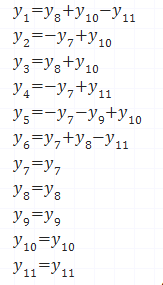
Рисунок 5 – Результат решения y*C методом Гаусса

Получив решение данной системы, проверим её живость и ограниченность с помощью таблицы:

Таблица 4 – Таблица значений y

Y1	Y2	Y3	Y4	Y5	Y6	Y7	Y8	Y9	Y10	Y11
1	0	2	0	-1	1	1	1	1	1	1
1	1	2	1	1	0	0	1	0	1	1

Если сложить 1 строку с двумя вторыми, то мы получим следующее значение:

Таблица 5 – Решение y*C

Y1	Y2	Y3	Y4	Y5	Y6	Y7	Y8	Y9	Y10	Y11
3	2	6	2	1	1	1	3	1	3	3

Таким образом у нас имеется полная P-цепь

Далее рассмотрим уравнение (2), согласно которому получаем:

Рисунок 6 – Система уравнений C*x

Рисунок 7 – Решение системы уравнений C*x (1)

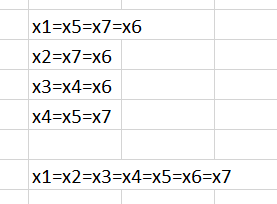
Рисунок 8 – Решение системы уравнений C*x (2)

Исходя из полученного выходит, что X = {1; 1; 1; 1; 1; 1; 1}

Значит мы имеет дело с полной T-цепью.

Так как мы имеем полную P-цепь и полную T-цепь, значит наша сеть Петри является живой и ограниченной.