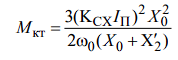Арефьев а.В.

1. Естественные электромеханическая и механическая характеристики располагаются в 1 квадранте, отличаются переменной жесткостью и имеют две зоны: практически линейная рабочая зона от точки ХХ до критического момента и пусковая нелинейная от точки со скольжением 1 до критического момента.

Для построения электромеханической характеристики АД проанализируем характерные точки этой зависимости и ее асимптоты, придавая скольжению s и скорости ω различные значения в пределах ±∞:

1. S=0, ω=ω₀, I₂`=0,I₁=I₀ – точка идеального холостого хода.

2. S=1, ω=0, I₁=I_кз`=Iп - точка короткого замыкания, пуска.

3. S=-R₂`/R<sub>1</sub>, ω=ω<sub>0</sub>(1-S<sub>1</sub>), I`₂=Imax=Uф/X_k – значения максимального значения тока ротора, лежащая в области отрицательных скольжений.

4. S→±∞, ω→∞, I₂`→I_∞=Uф/√(R1² +X²_k) – асимптотическое значение тока ротора при бесконечно большом увеличении скольжения и скорости.

Характерные точки механической характеристики:

1. S=0, ω=ω₀, M=0 – параметры идеального холостого хода.

2. S=1, ω=0, M=M_кз=М_п – значения короткого замыкания.

3. S=S_кл, M=M_кд, S=-S_k2, M=-M_k2 – точки экстремума.

4. S→±∞, ω→∞, M→0 – асимптота механической характеристики, которой является ось скорости.

Формулы для электромеханической и механической характеристик:

;

.

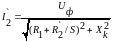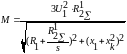2. Регулирование сопротивления ротора

Зависимость располагается в первом квадранте и имеет нелинейный вид. Скорость ХХ и критический момент остаются неизменными, критическое скольжение увеличивается.

Уравнения для определения скорости холостого хода, критического момента и критического скольжения:

;

;

.

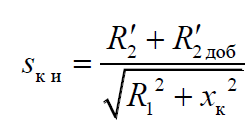При этом методе жесткость характеристики уменьшается.

Плавность и диапазон регулирования маленькие.

3. Торможение противовключением.

График для данного режима работы находится в IV квадранте и характеризуется скольжением, большим либо равным 1, имеет нелинейный вид. Суть метода заключается в изменении порядка подключения фаз АД. Поле статора начинает вращаться в противоположную сторону относительно вращения ротора.

Сергеев а.С.

1. Естественные характеристики.

Зависимости ω=f(M) и ω=f(I) были получены при номинальных параметрах электрической машины. Графики имеют вид кривых, располагаются в первом квадранте.

Особенные точки зависимости ω=f(I):

1. S=0 при скорости ω₀ ток ротора I₂`=0, I₁=I₀ – идеальный холостой ход.

2. S=1 при клине вала ω=0, I₁=I_кз`=Iп – короткое замыкание.

3. S=-R₂`/R<sub>1</sub>, ω=ω<sub>0</sub>(1-S<sub>1</sub>), I`₂=Imax=Uф/X_K – максимальный ток ротора.

4. S→±∞, ω→∞, 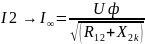– асимптотическое значение тока ротора при бесконечно большом увеличении скольжения и скорости.

Характерные точки зависимости s=f(М):

1. S=0 при скорости ω₀, M=0 – идеальный холостой ход.

2. S=1, ω=0, M=M_кз=М_п – короткое замыкание.

3. S=S_кл, M=M_кд, S=-S_K2, M=-M_k2 – точки экстремума.

4. S→±∞, ω→∞, M→0 – асимптота механической характеристики, которой является ось скорости.

Механическую характеристику можно разделить на 2 участка

1-й участок – прямая зависимость от ω₀ до ω при М_K.

2-й участок – криволинейный от ω при М_K до приближения скорости к бесконечности.

Уравнения электромеханической и механической характеристики имеют вид:

;

.

2. Введение доп. сопротивлений в цепь статора.

Зависимость имеет криволинейный вид, располагается в первом квадранте. Скорость холостого хода не изменяется относительно естественной характеристики, уменьшается критический момент и критическое скольжение, а также модуль жесткости механической характеристики и стабильности угловой частоты вращения.

Формулы для скорости холостого хода, критического момента и критического скольжения:

;

.

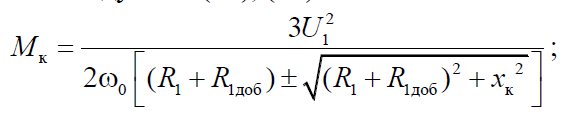
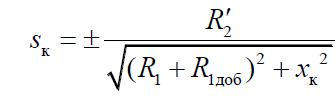Плавность и диапазон регулирования небольшие.

3. Динамическое торможение.

Характеристики имеют криволинейный вид, расположены во втором квадранте.

Динамическое торможение происходит следующим образом: обмотку статора отключают от сети переменного тока и подключают к источнику постоянного тока. Обмотка ротора при этом может быть замкнута накоротко или в её цепь включается добавочный резистор. Взаимодействие тока ротора с результирующим магнитным полем (поток в обмотке статора и ротора) двигателя создаёт тормозной момент, за счёт чего достигается эффект торможения. Двигатель работает в режиме динамического торможения независимо от сети, преобразовывая механическую энергию движущихся частей в электрическую, которая рассеивается в виде тепла в цепи ротора.

Механическую характеристику АД при динамическом торможении можно определить по формуле:

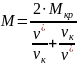
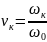– относительная критическая скорость;

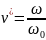– относительная скорость при торможении;

Максимальный критический момент при динамическом торможении: