
Lb1
.docxМинистерство науки и высшего образования Российской Федерации
Федеральное государственное автономное образовательное учреждение высшего образования
«Национальный исследовательский Томский политехнический Университет»

Инженерная школа энергетики
Отделение электроэнергетики и электротехники
Направление: 13.03.02 Электроэнергетика и электротехника
Знакомство с пакетом MATLAB и его приложением SIMULINK
Лабораторная работа №1
Вариант – 8
по дисциплине:
Математическое моделирование в электротехнике
Выполнил: :
|
|
||||
студент гр. 5А96 |
|
|
Сергеев А.С. |
|
01.02.2024 |
|
|
|
|
|
|
Проверил:
|
|
||||
доцент ОЭЭ ИШЭ |
|
|
Воронина Н.А. |
|
|
|
|
|
|
|
|
Томск – 2024
Цель работы: изучить возможности пакета Matlab и его приложения Simulink.
Программа работы
Ознакомиться с пакетом Matlab по его описанию в литературе.
Ознакомиться с приложением Simulink по его описанию в литературе.
Ознакомиться с языком Matlab.
Опробовать режимы работы: диалоговый (режим калькулятора), программирования (написание программ в виде m-файлов), визуального моделирования.
Построить имитационную модель системы «источник постоянного напряжения – электрическая R-L цепь».
Оформить отчет, отражающий результаты по каждому пункту работы.
Необходимо ознакомиться с возможностями Matlab. Для этого создаем m-файл, и производим простейшие вычисления. Примеры вычислений приведены на рисунках 1-

Рис. 1 Вычисления в m-файле

Рис. 2 Вычисления в m-файле

Рис. 3 Вычисления в m-файле
Далее ознакомимся с возможностью построения графиков в командной строке и в m-файле. По результатам построения видно, что оба графика совпадают.
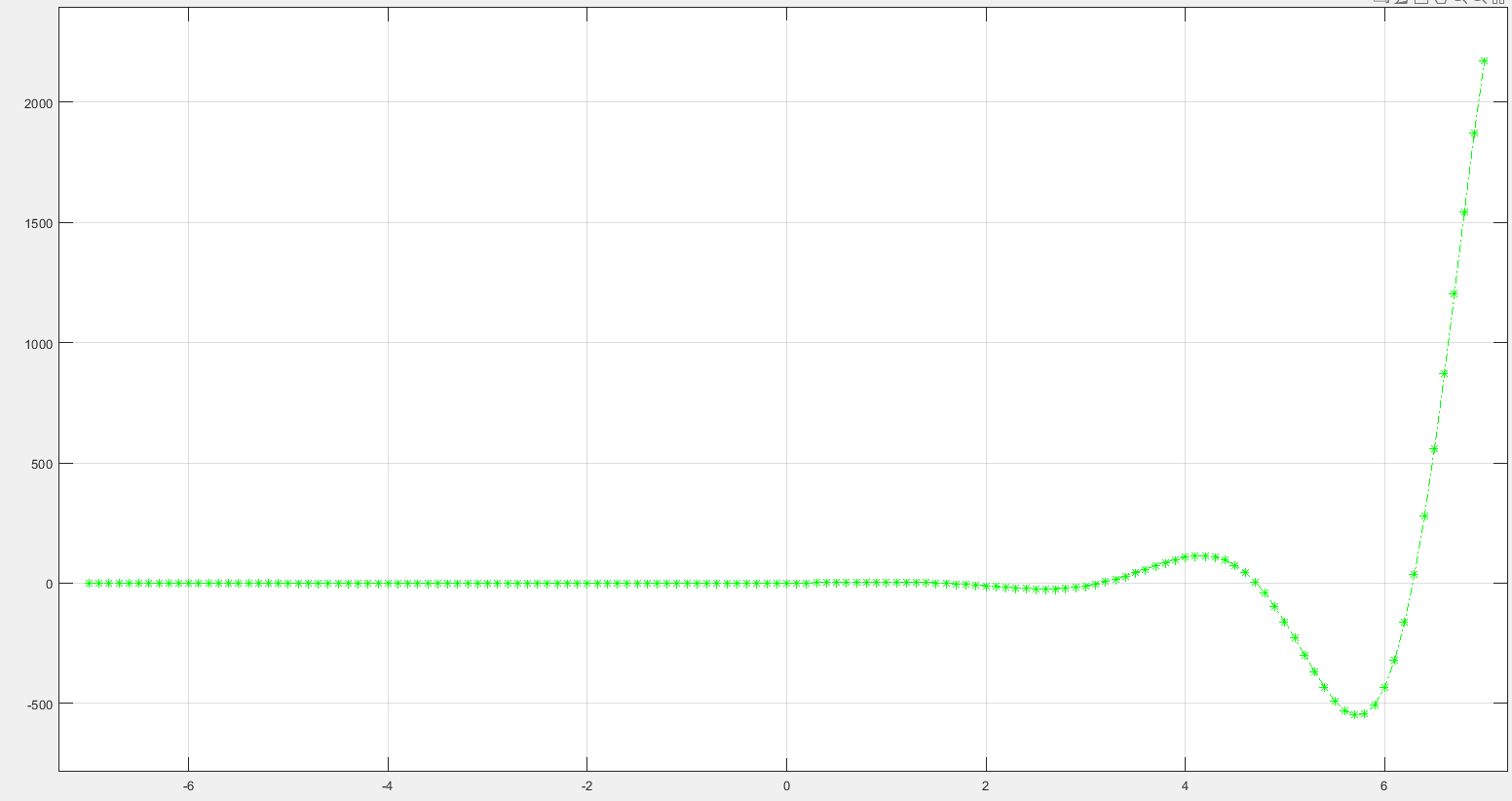
Рис. 4 График, построенный с помощью командной строки
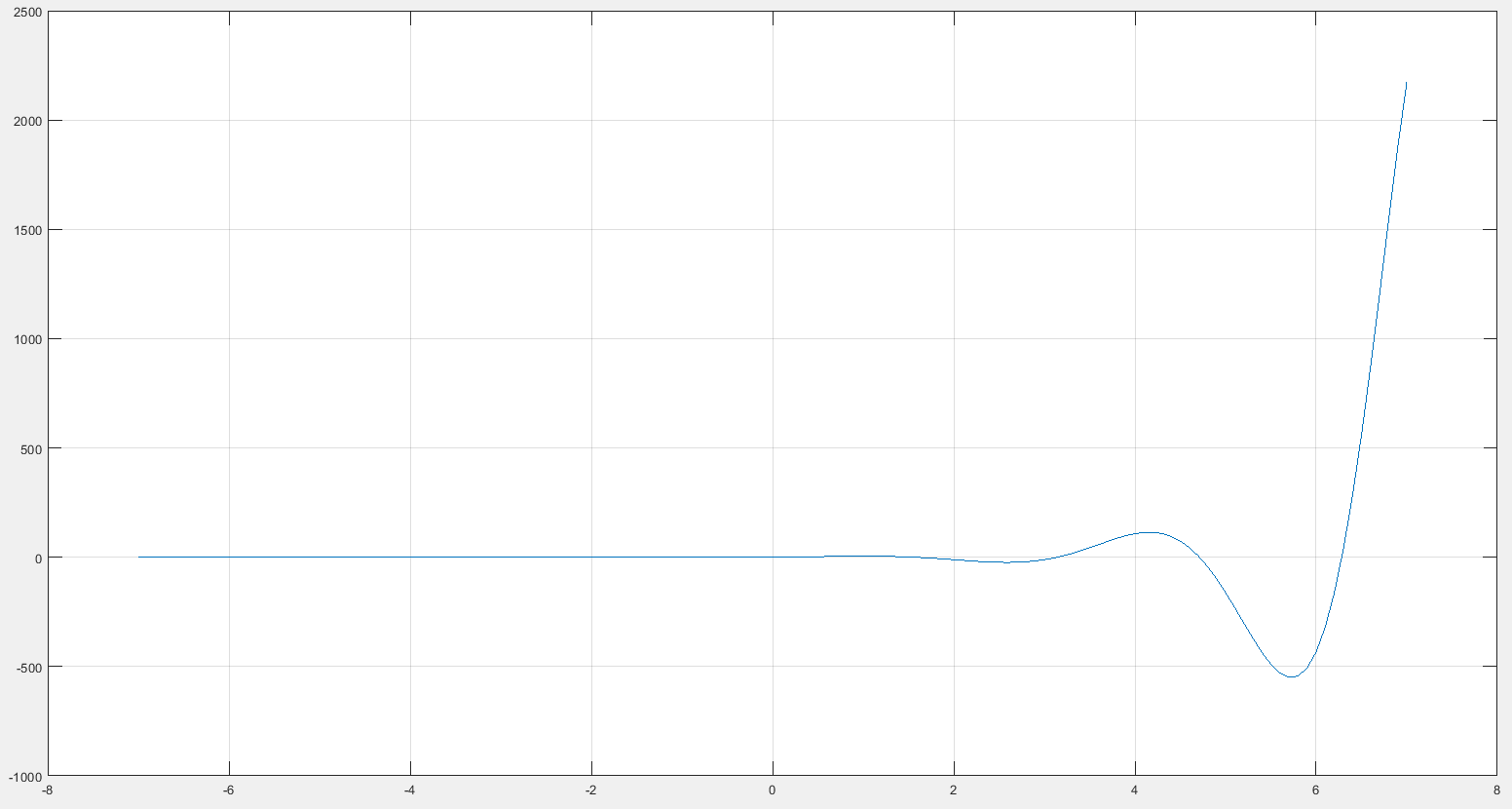
Рис. 5 График, построенный в m-файле
Для построения синусоиды воспользуемся m-файлом. Запись функции и порядок оформления графика представлен на рисунке 6.

Рис. 6 Запись функции в m-файле
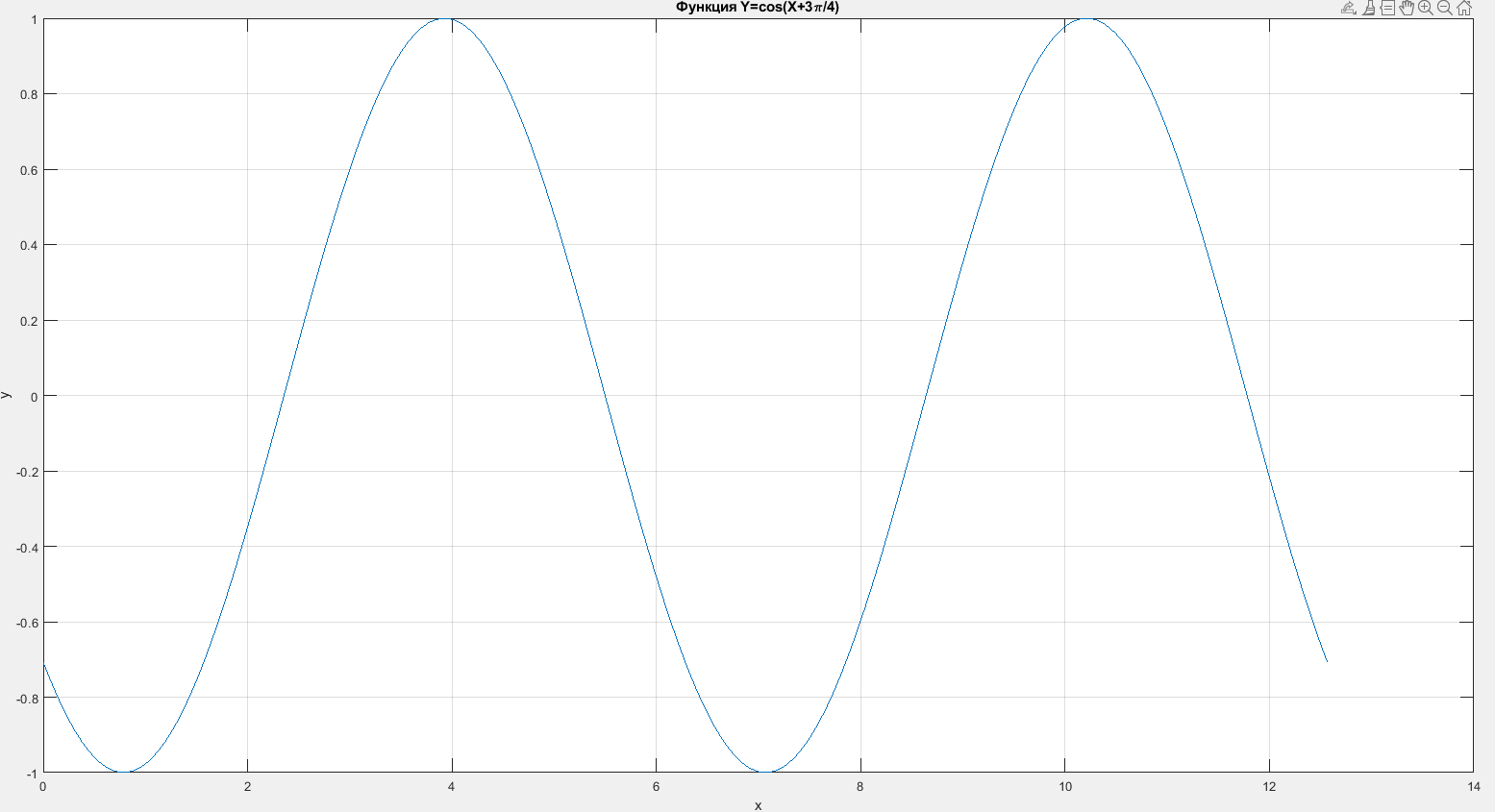
Рис. 7 График синусоиды
Исходные данные для выполнения работы представлены в таблице 1.
Таблица 1. Исходные данные
Вариант |
U, В |
R, Ом |
L, Гн |
8 |
115 |
45 |
1,5 |
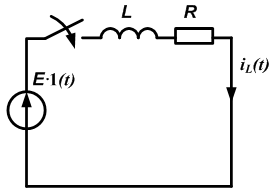
Рис. 1 – Схема RL-цепи
Численный метод Эйлера
Численные методы позволяют найти частное решение как обыкновенных дифференциальных уравнений, так и уравнений в частных производных. Метод Эйлера – алгоритм вычисления приближенного значения неизвестной функции на некоторой выбранной сетке аргументов.
На рисунке 4 предоставлена программа, написанная в Mathcad для решения уравнений методом Эйлера.
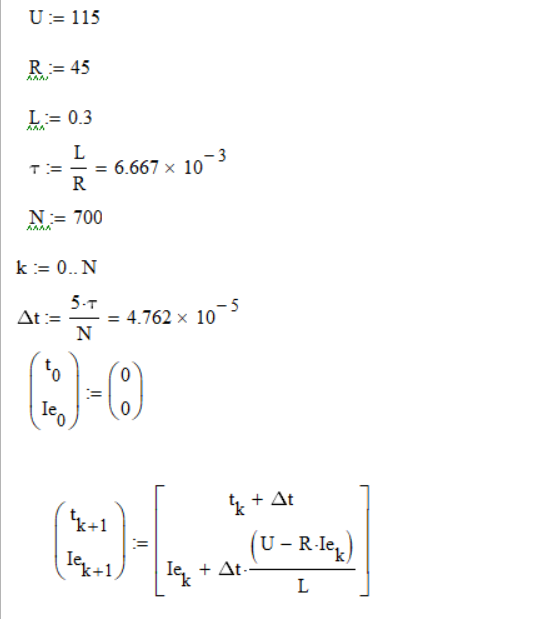
Рис. 4 – Листинг программы в Mathcad
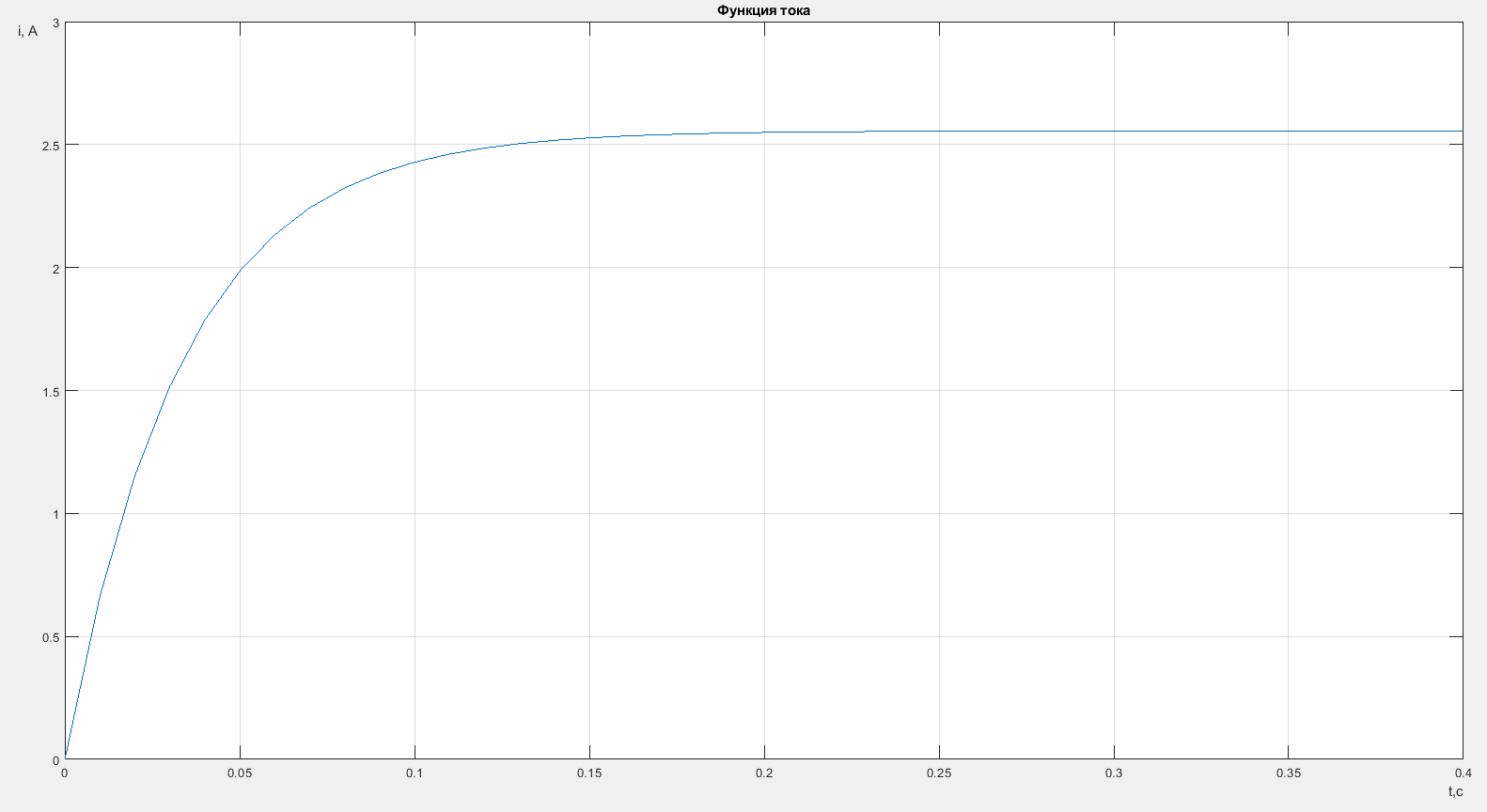
График переходного процесса в результате моделирования предоставлен на рисунке 5.
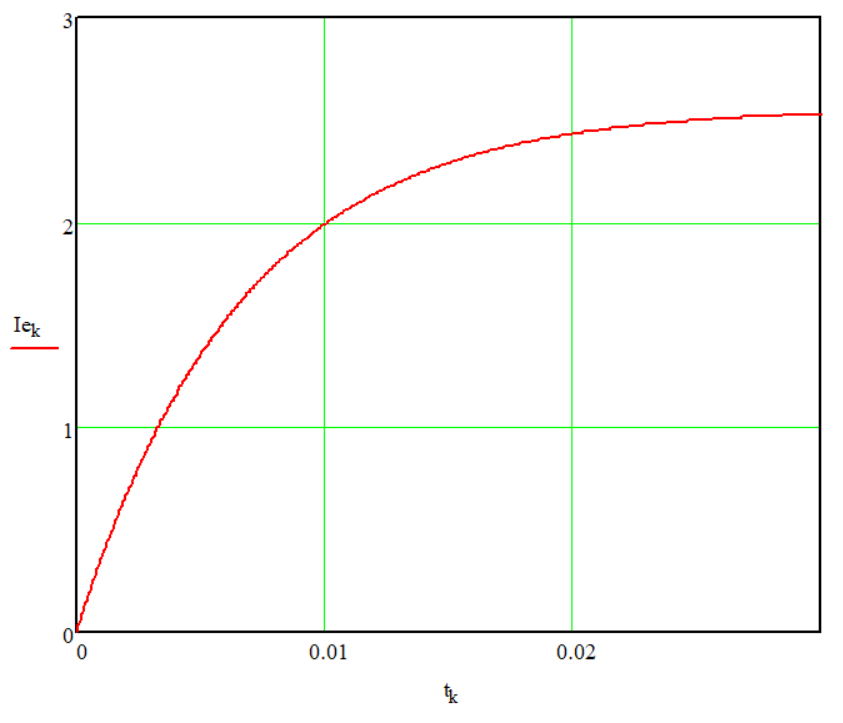
Рис.5 – График переходного процесса RL-цепи
Операторный метод.
При помощи преобразований Лапласа для уравнений, составленных с использованием законов Кирхгофа, решим систему уравнений операторным методом в программном продукте Mathcad.
Листинг программы представлен на рисунке 6.
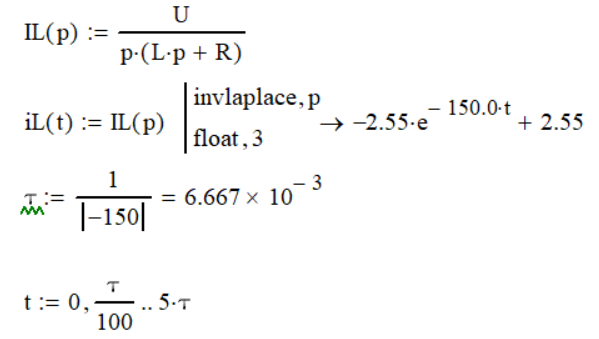
Рис. 6 – Текст программы в программе Mathcad
Результаты выполнения программы представлены на рисунке 7.
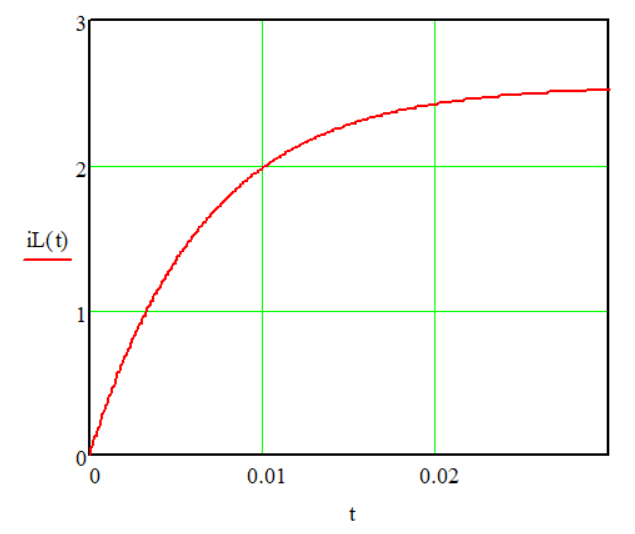
Рис.7 – Переходный процесс в RL-цепи
Моделирование RL-цепи в программном продукте Matlab Simulink.
На рисунке 8 представлена имитационная модель RL-цепи.
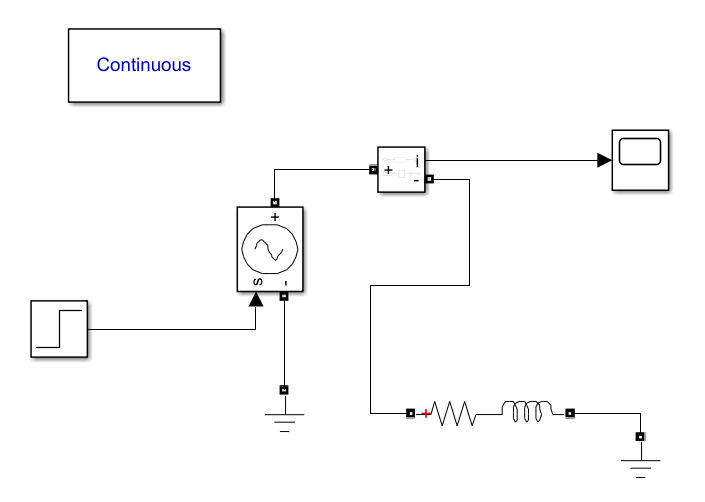
Рис. 8 – Имитационная модель RL-цепи
Результаты моделирования представлены на рисунке 9.
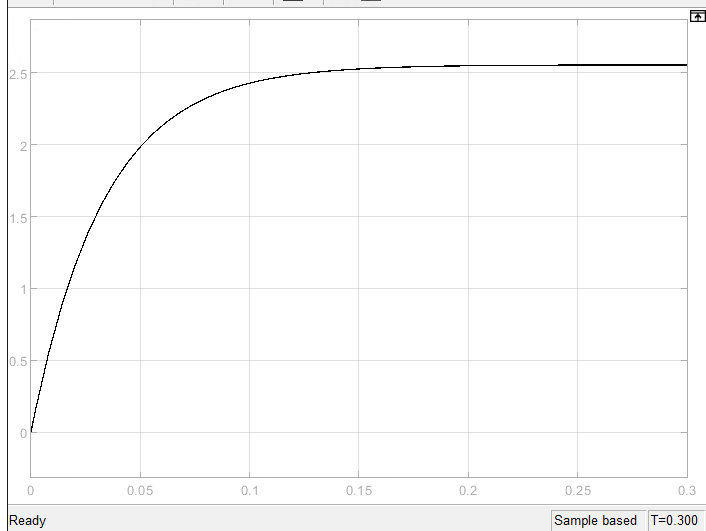
Рис.9 – График переходного процесса RL-цепи
Метод Рунге-Кутта.
Решим дифференциальное уравнение переходного процесса Рунге-Кутта методом, строим кривую переходного процесса. С помощью программы, записанной как файл-сценарий и файл-функция.
На рисунке 12 представлен программа, записанная как файл-сценарий.
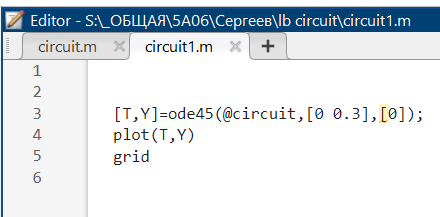
Рис. 12 – Файл-сценарий
На рисунке 13 представлен программа, записанная как файл-функция.
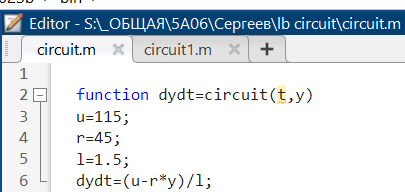
Рис.13 – Файл-функция
На рисунке 12, 13 были представлены решения дифференциального уравнения методом Ронге-Кутта.
Кривая переходного процесса представлена на рисунке 14.
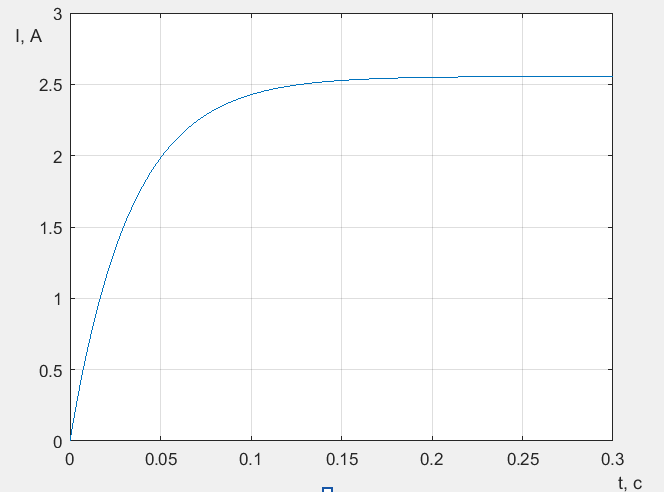
Рис.14 – Кривая переходного процесса
Метод Эйлера.
Напишем программу решения дифференциального уравнения методом Эйлера используйте оператор цикла.
На рисунке 15 представлен программа решения.
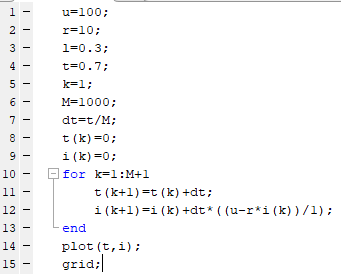
Рис.15 – Программа решения
Строим кривую переходного процесса представленный на рисунке 16.
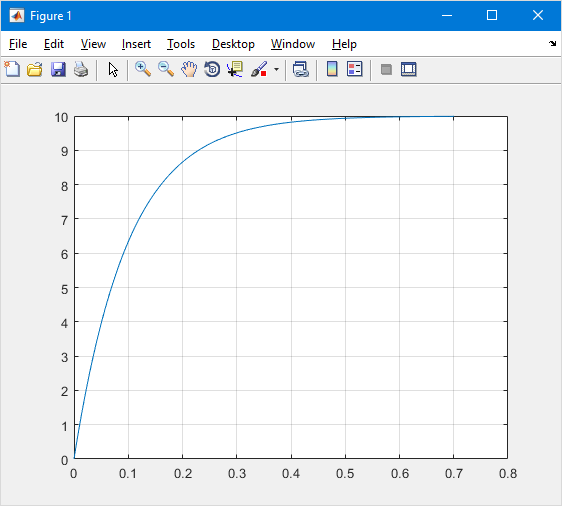
Рис.16 – Кривая переходного процесса
Вывод: Исходя из результатов моделирования делаем вывод, что структурные схемы составлены верно, т.к. графики переходных процессов и значения токов аналогичны друг другу. Использование того или иного метода обусловлено лишь областью его применения, а также плюсами и минусами. Однозначно выбрать «самый удобный» или «самый неудобный» метод нельзя.
