1.Основные теоретические модели процесса массоотдачи (пленочная, проникновения, диффузионного пограничного слоя).

Пленочная модель:

C₀ – концен.целевого компонента; Cгр* - концен.коипонента на границе раздела фаз. Основные допущения:1.Процесс стационарный; 2.Задача одномерная; 3.Движения в пленке нет(либо не движется, либо ламинарно);4.На границе существует пограничный диффузионный слой.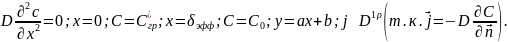 2.Диффузионно-пленочная модель. В этой модели сравниваются уравнение Новье-Стокса и второй закон Фика, с математической точки зрения они ничем не отличаются С упрощением эти уравнения были решены и были получены профили скорости и концентрации поперечной области(область расположенная вдали от поперечной координаты) – мера отношений импульса к переносу массы. – отношение пограничного диффузионного слоя к толщине пограничного слоя при гидродинамике равно . Pr по теплообмену и Pr диффузионный для газов близки к 1, таким образом . Для жидкости Pr близок к 100 (диффузионный)=> . 3.Модель Хигби(Теория обновления поверхности). По этой теории идут постоянные пульсации, они пробивают границы раздела фаз и приносят некоторый объем вещества и распластываются в виде лепешки на стенке, далее идет диффузия. Между пульсациями идет диффузия с новыми принесенными веществами(поток уменьшается). Локальная неизвестная- это изменение концентрации во времени. Диффузия идет через границу, темп постепенно уменьшается. 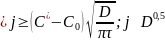Меняется только коэффициент , а суть остается прежней. Экспериментальные данные по массообмену показывают, что поток будет близок к (правда несколько выше) пр:песок и сковорода.

2.Дифференциальное уравнение ковнективно-диффузионного переноса массы.

Выделим из исследуемой среды элементарный объем. Поток входит в этот объем следовательно меняется концентрация.Поток входит не по касательной, элементарный объем должен быть менше, чем исследуемое пространство, больше чем молекулы, чтобы сохранить сплошность и непрерывность, источника внутри нет, физико-химические свойства.. Поток состоит из двух составляющих конвективной и диффузионной.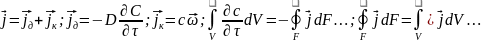 Подставим в уравнение (2) уравнение (3) и перенесем всё в левую часть:

Уравнение неразрывности потока связано с ρ и с изменением потока.

Были попытки усовершенствовать эту модель: 1) изменить коэффициент диффузии; 2) хотели ввести турбулентный коэффициент диффузии.

3.Движущая сила и направление масообменного процесса.

Массообменный процесс – это процесс при котором происходит переход компонента из одной фазы в другую.=>диффузионный пронос: распространение компонента из-за диффузии. Основные процессы: абсорбция, десорбция, ректификация, сушка, адсорбция, экстракция, кристаллизация, ионный обмен. Все массообменные процессы делят на 2 группы: 1.Массобменные процессы , где имеется подвижная граница раздела фаз (абсорбция, ректификация, экстракция). 2.Граница определена (сушка, ионный обмен). Так же массообмен можно разделить и по другому фактору: 1.Массообменный процесс, где один компонент А переходит из одной фазы в другую –фазы инертны.2.Переходы одной фазы в другую.( фазы не инертны – ректификация.) Движущая сила процесса – разность действительной (истинной , рабочей У) и равновесной У* концентраций целевого компонента. Чем значительнее действительная концентрация отличается от концентрации равновесной, тем больше скорость массопередачи, т.е. скорость стремления системы к состоянию равновесия. Движущая сила – мера отклонения процесса от состояния равновесия. Этот процесс идет самопроизвольно, мы можем его усилить или замедлить.Движущая сила процесса – это разность между текущей и равновесной. Для у_н нужно знать х_к и подставить его в 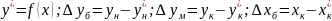Если численные значения действительных концентраций целевого компонента в двух контактирующих фазах соответствуют равновесному соотношению для рассматриваемой системы, то такая система находится в равновесном состоянии и направленного перехода компонента из одной фазы в другую не будет. Если же значения действительных концентраций в контактирующих фазах отличаются от значений, предписанных равновесным соотношением, то возникает направленный поток целевого компонента, стремящийся изменить действительные концентрации компонента в сторону приближения их к равновесному соотношению.