
- •1. Идеальные и неидеальные растворы. Закон Рауля.
- •2.Парциальные мольные величины, методы их определения. Уравнения Гиббса-Дюгема.
- •5 Вычисление активностей растворителя и растворенного вещества по давлению пара, понижению температуры замерзания, повышению температуры кипения и из-за осмотического давления.
- •7 )Растворимость газов в жидкостях. Закон Генри. Влияние давления и температуры на растворимость газов в жидкостях.
- •8.Неограниченно растворимые друг в друге жидкости. Вычисление давления и состава пара над идеальными растворами. Первый закон Гиббса-Коновалова.
- •10 Диаграммы общее давление – состав, температура кипения – состав, состав раствора – состав пара для неидеальных растворов. Азеотропные растворы. Второй закон Гиббса – Коновалова.
- •11. Перегонка (ректификация) растворов.
- •12. Ограниченная взаимная растворимость жидкостей. Влияние температуры на растворимость.
- •14. Давление и состав пара над смесью взаимно нерастворимых жидкостей. Перегонка с водяным паром.
- •15.Идеальная растворимость твердых веществ в жидкости (уравнение Шредера). Термический анализ кривые охлаждения.
- •1. Скорость реакции. Кинетическое уравнение. Константа скорости реакции, молекулярность и порядок реакции.
- •3,Способы определения порядка реакции
- •4.Сложные реакции: двухсторонние (обратимые), сопряженные.
- •5, Сложные реакции: параллельные, последовательные.
- •6. Стадийное протекание реакций. Метод квазистационарных концентраций. Механизм мономолекулярных реакций, протекание их по 1-му и 2-му порядкам.
- •7. Зависимость скорости реакции от температуры, уравнение Аррениуса. Энергия активации.
- •8,Теория активных соударений. Выражение для константы скорости по теории активных соударений. Стерический фактор.
- •10 Сопоставление уравнений теории активных соударений и теории переходного состояния.
- •11. Влияние растворителя на скорость реакций в растворах. Роль сольватации. Гомо- и гетеролитические реакции.
- •12. Влияние ионной силы раствора на скорость реакций в растворах, солевой эффект. Уравнение Бренстеда.
- •13,Цепные реакции.(цп) Особенности цепных реакций. Возникновение, развитие и обрыв цепей.
- •15 Фотохимические реакции. Закон фотохимической эквивалентности а.Эйнштейна. Квантовый выход кинетика фотохимических реакций.
- •16. Стадии гетерогенного процесса. Диффузия в газах, жидкостях и твердых телах. Законы Фика.
- •17. Соотношение диффузионных и кинетических факторов в гетерогенной кинетике. Влияние температуры и перемешивания на режим гетерогенного процесса.
- •18,Гомогенный катализ, механизм. Кислотно-основной, ферментативный катализ.
- •20 Стадии и теории гетерогенного катализа.
- •1. Коллигативные свойства растворов электролитов. Изотонический и осмотический коэффициенты. Влияние растворителей на диссоциацию.
- •2. Основы электростатической теории сильных электролитов Дебая и Хюккеля. Вычисление коэффициентов активности. Ионные и средние ионные коэффициенты активности.
- •3.Равновесия в растворах электролитов. Термодинамические и практические константы равновесия, влияние ионной силы.
- •4.Электрическая проводимость растворов. Удельная, молярная проводимость. Связь электрической проводимости с подвижностями ионов.
- •5 Зависимость электрической проводимости от концентрации; предельная молярная проводимость.
- •6. Зависимость электрической проводимости от температуры, природы электролита и растворителя.
- •7.Числа переноса, их использование для определения электрической проводимости ионов.
- •8,Основные положения теории электрической проводимости сильных электролитов Дебая-Хюккеля-Онзагера.
- •10 Механизмы возникновения скачка потенциала и двойного электрического слоя на границе раздела металл – раствор электролита.
- •11. Электрохимический потенциал. Выражение для равновесного скачка потенциала на границе металл – раствор электролита.
- •12. Гальванические элементы. Электродвижущие силы электрохимических систем. Водородная шкала электродных потенциалов.
- •13,Выражение равновесного потенциала для электродов различных типов (электроды первого и второго рода, окислительно-восстановительные).
- •15 Использование стандартных потенциалов для определения направления химических и электрохимических реакций.
- •16. Определение δg, δs, δh и константы равновесия реакции, протекающей в гальваническом элементе. Термодинамический расчет эдс.
- •17. Практическое использование потенциометрических измерений.
- •18,Электролиз. Катодные и анодные процессы. Характеристика скорости электрохимических процессов с помощью поляризационных кривых.
- •[Править]Растворы
Термодинамика.
1. Идеальные и неидеальные растворы. Закон Рауля.
Раствор – гомогенная (однофазная) смесь 2-х и более в-в.
Р-ры м. б. образованы следующим образом: г-г, ж-ж, т-т, г-ж, г-т, ж-т. Р-ры отличаются от гетерогенной смеси размерами частиц: r(гомогенного р-ра) < 1 нм, r(гетерогенной смеси) > 10 нм, 1 нм < r(коллоидной частицы) < 10нм.
Р-р отличается от хим. соединения: - переменностью состава; - характером взаимодействия.
Существует 2 теории р-ров: Менделеева (хим. взамодействия) и Алексеева (В-д-В силы).
Идеальные р-ры – те, у кот. отсутствуют взаимодействия (этим и отличаются от реальных)
Пусть есть однокомпонентная система: 1 (растворитель). Существует равновесие: ж(1)↔п(1). Мольная доля Х1 = 1, давление чистого растворителя над чистым раст-лем: Р0,1
Добавим
второй компонент 2.
Равновесие: ж(1,2)↔п(1).
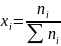 .
Давление чистого р-ля над р-ром при этом
P1<
Р0,1, Х1
< 1,
.
Давление чистого р-ля над р-ром при этом
P1<
Р0,1, Х1
< 1, 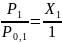 , → Для
ид.р-ра: P1=Р0,1∙
Х1 →
, → Для
ид.р-ра: P1=Р0,1∙
Х1 → 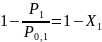 ,
при
чем
,
при
чем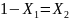 → Закон
Рауля
для ид. р-ров:
→ Закон
Рауля
для ид. р-ров:
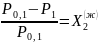 ,
где (ж) – «относится к жидкой фазе».
,
где (ж) – «относится к жидкой фазе».
Относительное понижение давл. пара растворителя над р-ром прямо пропорционально концентрации раств-го в-ва. Закон Рауля справедлив и для р-ля и для раств-го в-ва.
Близки по св-вам к ид. р-рам предельно разбавленные реальные р-ры:
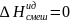 , изменение
объема (смешение):
, изменение
объема (смешение):
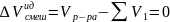 (образование
ид. р-ра не сопровождается тепловым
эффектом и изменением объема)
(образование
ид. р-ра не сопровождается тепловым
эффектом и изменением объема)
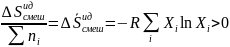 ,
где
,
где
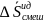 –
парциальная
мольная величина смешения.
–
парциальная
мольная величина смешения.
→ 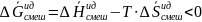 ,
что характерно для произвольного
процесса.
,
что характерно для произвольного
процесса.
Для предельно разб-х р-ров: P1=Р0,1∙ Х1 – для растворителя, P2~Х2, Р0,2≠K
Закон Генри: P2 = K∙Х2 (для растворенного в-ва в пред. разб. р-ре), где K – постоянная Генри.
Считаем, что E1-1≈ E2-2≈ E1-2, ΔVсмеш = 0, ΔНсмеш = 0
В
остальных сл. используется не закон
Рауля, а з-н
Маргулеса:
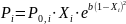
Среди
неидеальных выделяют: регулярные
и атермальные р-ры.
Образование регулярных
р-ров
происходит с тепловым эффектом и
изменением объема:
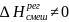 ,
, 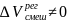 ,
, 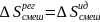
Образование
атермальных
р-ров
происходит без выделения тепла:
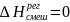 ,
,
,
,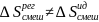 E1-1≠
E2-2
≠E1-2
E1-1≠
E2-2
≠E1-2
2.Парциальные мольные величины, методы их определения. Уравнения Гиббса-Дюгема.
M(экстенсивные свойства,т.е. зависящие от ко-ва в-ва):H,U,A,G,S,C,V.
M=f(P,T,n1,n2...ni)
P,T=const
dM=(M/n1)p,t,n2,n3...ni+(M/n2)p,t,n1,n3...ni+…+(M/ni)p,t,n1..ni-1
(M/ni)p,t,nji=M*i-парциальная мольная величина
dM=M*idni-первое уравнение Гиббса-Дюгема(изменение св-ва по со-ву)
Порциальная мольная величина-изменение экстенсивного св-ва при изменении ко-ва данного в-ва при условии постоянства давления,температуры и ко-ва всех основных компонентов. Например,возьмем: M=V dV=V*1dn1+V*2dn2 V=V*1n1+V*2n2 o/mdM=o/niM*idni M=M*ini
M/ni=M* и ni/ni=Xi M*=M*iXi
Продиф. Без ограничения: dM=M*idni+nidM*i
nidM*i=0 XidM*i=0 Св-ва парциальных мольных величин: 1)ПМВ явл-ся не св-ми,а отражают изменение св-в при изменении….сос-ва. 2)ПМВ относятся к конкретному составу. … 3)м/у ПМВ соблюдаются те же соотношения,что и м/у мольными…величинами. Способы...определения…ПМВ: 1)аналитически Например: M=a+bn2+cn2^2+dn2^3,где индекс 2-растворенное…в-во M=(M/n2)p,t=b+2cn2+3dn2^2 2)графический a)M*2=tg1=M/m20 M*2=tg20
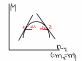
б)метод отрезков
ab`/ac`=bb`/cc`
X2/1=(M*-M*1)/(M*2-M*1)
M*=M*1x1+M*2x2
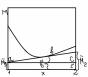
3.Химический потенциал компонента в идеальном и неидеальном растворах.
µi = (∂G / ∂ni) P ,T, nj ≠ i= G͞i -порциальная мольная энергия Гиббса µi = (∂H / ∂ni) P ,S, nj ≠ I = (∂A / ∂ni) V ,T, nj ≠ I =(∂u / ∂ni) V ,S, nj ≠ I= M͞–порциальная мольная величина (∂H / ∂ni) P ,T, nj ≠ I = H͞i Рассмотрим 3-е уравнение Гиббса-Дюгема
![]()
Для
2-х компанентных растворов
![]() Рассмотрим условия равновесия
Жидкость(1)nар(1)
(когда чистый растворитель)
µ
Рассмотрим условия равновесия
Жидкость(1)nар(1)
(когда чистый растворитель)
µ ж
0,1
=µп0,1=µ01+RT
ln
p0.1
; p0,1-
приведённое давление
Если
ж(1,2) п(1)
µж
1
=µп1=µ01+RT
ln
p1
Вычтем
1-ое из 2-го
µж1-µ0,1=RT
ln(
p1/p0.1)
Для
компанента ид. Раствора
µж
1
=µж0,1+RT
ln
x1
Для каждого компанента
ид.раствора
µжi
=µ0,i+RT
ln
xi
=µ0,I,m+RT
ln
mi=µ0,Ic+RT
ln
ci
m
i→µ0,
1 m
; c
i→µ0,
1 c
µ0
.im
≠
µ0,
I,
c
≠
µ0
, I
c
Для неидеал. Растворов
µi=µ0,
1+RT
ln (fi/f
0,
i)=
µ0
, i +RT
ln a i
ж
0,1
=µп0,1=µ01+RT
ln
p0.1
; p0,1-
приведённое давление
Если
ж(1,2) п(1)
µж
1
=µп1=µ01+RT
ln
p1
Вычтем
1-ое из 2-го
µж1-µ0,1=RT
ln(
p1/p0.1)
Для
компанента ид. Раствора
µж
1
=µж0,1+RT
ln
x1
Для каждого компанента
ид.раствора
µжi
=µ0,i+RT
ln
xi
=µ0,I,m+RT
ln
mi=µ0,Ic+RT
ln
ci
m
i→µ0,
1 m
; c
i→µ0,
1 c
µ0
.im
≠
µ0,
I,
c
≠
µ0
, I
c
Для неидеал. Растворов
µi=µ0,
1+RT
ln (fi/f
0,
i)=
µ0
, i +RT
ln a i
4. Активность и коэффициент активности. Выбор стандартного состояния для растворителя и растворенного вещества.
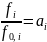 -
активность, где
-
активность, где
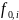 –
фугитивность(летучесть) чистого
растворителя
–
фугитивность(летучесть) чистого
растворителя
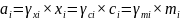 ,
где
,
где
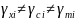 – коэффициенты
активности
– коэффициенты
активности
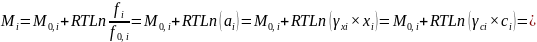
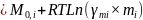
Стандартное
состояние для идеального раствора:
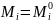 (Химический потенциал равен своему
стандартному значению), если :
(Химический потенциал равен своему
стандартному значению), если :
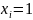 ,
то
,
то
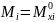
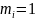 ,
то
,
то
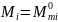
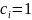 ,
то
,
то
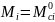
Не идеальный раствор:
Симметричное стандартное состояние (стандартное состояние выбирается одинаково и для растворителя и для растворенного вещества)
,
если
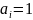 и
и
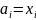 ,
,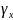 =1
=1
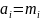 ,
,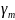 =1
=1
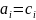 ,
,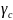 =1
=1
Несимметричное стандартное состояние (для растворителя одно, а для растворенного вещества другое)
Для растворителя:
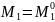 ,
если
,
если
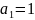 и
и
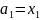 ,
,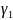 =1
=1
Для растворенного вещества:
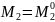 ,
если
,
если
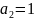 и
и
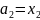 ,
,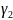 =1
=1
Берется
гипотетический раствор с концентрацией
равной 1, и свойствами предельно
разбавленного раствора (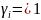 )
)
Физический смысл коэффициентов активности:
Коэффициент активности компонентов раствора характеризует работу, которую нужно затратить, чтобы перенести 1 моль i-го компонента из реального раствора в идеальный.
